海淀区初二期末数学

【www.guakaob.com--初二】

海淀区初二期末数学(一)
北京市海淀区2015-2016年八年级(上)册期末数学试卷

2015-2016海淀区八年级第一学期期末练习

数 学 2016.1

一、选择题（本题共36分，每小题3分）

在下列各题的四个备选答案中，只有一个符合题意．请将正确选项前的字母填在表格中相应的位．．置．

1．下列标志是轴对称图形的是（ ）

A B C D

002 5用科学记数法表示为（ ）

A．2.5106 B．0.25106 C．25106 D．2.5106

2

3．使分式有意义的x的取值范围是（ ）

x3 A．x3 B．x3 C．x3 D．x3 4．下列计算中，正确的是（ ）

A．(a2)3a8 B．a8a4a2 C．a3a2a5 D．a2a3a5 5．如图，△ABC≌△DCB，若AC＝7，BE＝5，则DE的长为（ ） A．2 B．3 C．4 D．5

6．在平面直角坐标系中，已知点A（2，m

）和点

B（n，－3）关 于x轴对称，则mn的值是（ ）

A．－1 B．1 C．5 D．－5

7．工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度．．分别与点M，N重合，过角尺顶点C作射线OC．由此作法便可得△MOC≌△NOC，其依据是（ ）

A．SSS B．SAS C．ASA D．AAS

2．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，2.5微米等于0.000 002 5米，把数字0.000

8．下列各式中，计算正确的是（ ）

x31

2

x9x3

22

C．(a2)a4 D． (x2)(x3)x2x6

A．x(2x1)2x21 B．

9．若ab1，则a2b22b的值为（ ） A．4 B．3 C．1 D．0

10．如图，在△ABC中，AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于

D点，则∠DBC的度数是（ ）

A．20° B．30° C．40° D．50° 11．若分式

6

的值为正整数，则整数a的值有（ ） a1

A．3个 B．4个 C．6个 D．8个 12．如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的

垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边 的中点，点M为线段EF上一动点，则△CDM周长的最小值为（ ）

A．6 B．8

C．10 D．12

二、填空题（本题共24分，每小题3分） 13．当xx

值为0． x1

14．分解因式：x2y4y x

15．计算：3

3y

2

16．如果等腰三角形的两边长分别为3和7，那么它的周长为．

17．如图，DE⊥AB，∠A＝25°，∠D＝45°，则∠ACB的度数为

18．等式(ab)2a2b2成立的条件为

19．如图，在△ABC中，BD是边AC上的高，CE平分∠ACB，交BD于点E，

DE＝2，BC＝5，则△BCE的面积为．

20．图1是用绳索织成的一片网的一部分，小明探索这片网的结点数（V），网眼数（F），边数（E）

之间的关系，他采用由特殊到一般的方法进行探索，列表如下：

表中“☆”处应填的数字为 ；根据上述探索过程，可以猜想V ，F， E之间满足的等量关系为 ；

如图2，若网眼形状为六边形，则V ，F， E之间满足的等量关系为 ．

图1 图2

三、解答题（本题共16分，每小题4分） 1

21(π3)3．

2

1

22．如图，E为BC上一点，AC∥BD，AC＝BE，BC＝DB．

求证：AB= ED．

2x23x423．计算：2． 2

x1x1x2x1

24．解方程：

x3

． 1

x1x1

四、解答题（本题共13分，第25题4分，第26题5分，第27题4分） 25．已知xy3，求[(xy)2(xy)(xy)]2x的值．

26．北京时间2015年7月31日，国际奥委会主席巴赫宣布：中国北京获得2022年第24届冬季奥林

匹克运动会举办权．北京也创造历史，成为第一个既举办过夏奥会又举办冬奥会的城市，张家口也成为本届冬奥会的协办城市．近期，新建北京至张家口铁路可行性研究报告已经获得国家发改委批复，同意新建北京至张家口铁路，铁路全长约180千米．按照设计，京张高铁列车的平均行驶速度是普通快车的1.5倍，用时比普通快车用时少了20分钟，求高铁列车的平均行驶速度．

27．已知：如图，线段AB和射线BM交于点B．

（1）利用尺规完成以下作图，并保留作图痕迹（不写作法）．

①在射线BM上作一点C，使AC＝AB； ②作∠ABM的角平分线交AC于D点；

③在射线CM上作一点E，使CE＝CD，连接DE．

（2）在（1）所作的图形中，猜想线段BD与DE的数量关系，并证明．

A

B

M

海淀区初二期末数学(二)
2016年北京市海淀区初二数学期末统考试题含答案

海淀区八年级第二学期期末练习

数 学

（分数：100分 时间：90分钟） 2016.7

学校 班级 姓名 成绩 一、选择题：（本题共30分，每小题3分）

在下列各题的四个备选答案中，只有一个是正确的． ．．．．1．下列各式中，运算正确的是

A

．3 B

 C

． D

2

2．下列各组数中，以它们为边长的线段不能构成直角三角形的是

A．1

B．3，4，5 C．5，12，13 D．2，2，3 3．如图，矩形ABCD中，对角线AC，BD交于O点．若∠AOB＝60°， AC＝8，则AB的长为

A．4 B

． C．3 D．5

4．已知P1（－1，y1），P2（2，y2）是一次函数yx1图象上的两个点，则y1，y2的大小关系是 A．y1y2 B．y1y2 C．y1y2 D．不能确定

5．2022年将在北京—张家口举办冬季奥运会，很多学校开设了相关的课程．下表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差s

2 根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择 A．队员1 B．队员2 C．队员3 D．队员4 6．用配方法解方程x22x30，原方程应变形为

A．(x1)22 B．(x1)

24 C．(x1)24 D．(x1)22 7．如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F，若BF＝12，AB＝10，则AE的长为 A．13 B．14 C．15 D．16

8．一个有进水管与出水管的容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分钟的进水量和出水量是两个常数，容器内的水量y（单位：L）与时间x（单位：min）之间的关系如图所示．则8min时容器内的水量为 A．20 L B．25 L C．27L D．30 L

9．若关于x的方程kx2(k1)x10的根是整数，则满足条件的整数k的个数为 A．1个 B．2个 C．3个 D．4个

10．如图1，在菱形ABCD中，∠BAD＝60°，AB＝2，E是DC边上一个动点，F是AB边上一点，

∠AEF＝30°．设DE＝x，图中某条线段长为y，y与x满足的函数关系的图象大致如图2所示，则这条线段可能是图中的

A．线段EC B．线段AE C．线段EF D．线段BF

图1 图2

二、填空题：（本题共18分，每小题3分）

11．写出一个以0，1为根的一元二次方程

12．若关于x的一元二次方程x24xm0有两个不相等的实数根，则m的取值范围是 13．如图，为了检查平行四边形书架ABCD的侧边是否与上、下边

都垂直，工人师傅用一根绳子比较了其对角线AC，BD的长度，若二者长度相等，则该书架的侧边与上、下边都垂直，请你说出其中的数学原理 ．

14．若一次函数ykxb（k0）的图象如图所示，点P（3，4）在函数图象

上，则关于x的不等式kxb≤4的解集是 ．

15．如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，

若AB＝5，BC＝8，则EF的长为 ．

16．如图，正方形ABCD的面积是2，E，F，P分别是AB，BC，AC上

的动点，PE

D

P

C

F

A

E

B

三、解答题：（本题共22分，第17—19题每小题

4分，第20—21

题每小题5分） 17

．计算：

18．解方程：y(y4)12y．

19．已知x1是方程x23axa20的一个根，求代数式3a29a1的值．

20．在平面直角坐标系xOy中，一次函数的图象经过点A（2，3）与点B（0，5）． （1）求此一次函数的表达式；

（2）若点P为此一次函数图象上一点，且△POB的面积为10，求点P的坐标．

21．如图，四边形ABCD中，AB＝10，BC＝13，CD＝12，AD＝5，AD⊥CD，求四边形ABCD的面

积．

四、解答题：（本题共10分，第22题5分，第23题5分） 22．阅读下列材料：

北京市为了紧抓疏解非首都功能这个“牛鼻子”，迁市场、移企业，人随业走．东城、西城、海淀、丰台„„人口开始出现负增长，城六区人口2016年由升转降．

而现在，海淀区许多地区人口都开始下降。统计数字显示：2015年该区常住外来人口约为150万人，同比下降1.1%，减少1.7万人，首次实现了负增长．

和海淀一样，丰台也在2015年首次实现了常住外来人口负增长，同比下降1.4%，减少1.2万人； 东、西城，常住外来人口同样呈下降趋势：2015年东城同比下降2.4%，减少5000人，西城则同比下降5.5%，减少1.8万人；

石景山，常住外来人口近年来增速放缓，预计到2016年年底，全区常住外来人口可降至63.5万，比2015年减少1.7万人，首次出现负增长； „„

2016年初，市发改委透露，2016年本市将确保完成人口调控目标——城六区常住人口较2015年下降3%，迎来人口由升转降的拐点．

人口下降背后，是本市紧锣密鼓疏解非首都功能的大战略． 根据以上材料解答下列问题：

（1）石景山区2015年常住外来人口约为 万人；

（2）2015年东城、西城、海淀、丰台四个城区常住外来人口同比下降率最高的是 区；

根据材料中的信息估计2015年这四个城区常住外来人口数最多的是 区； （3）如果2017年海淀区常住外来人口降到121.5万人，求从2015年至2017年平均每年外来人

口的下降率．

23．如图，四边形ABCD是矩形，点E在CD边上，点F在DC延长线上，AE＝BF． （1）求证：四边形ABFE是平行四边形；

（2）若∠BEF＝∠DAE，AE＝3，BE＝4，求EF的长．

五、解答题：（本题共20分，第24题6分，第25—26题每小题7分）

24．如图1，将边长为1的正方形ABCD压扁为边长为1的菱形ABCD．在菱形ABCD中，∠A的

大小为α，面积记为S．

（1）请补全下表：

（2）填空：

由（1

）

可以发现单位正方形在压扁的过程中，

菱形的面积随着∠A大小的变化而变化，

不妨把单位菱形的面积S记为S(α)．例如：当α＝30°时，SS(30)SS(135)

1

；当α＝135°时，2

．由上表可以得到S(60)S( ______°)；S(150)S( ______°)，„，由此可以归纳出S(180)S()．

（3） 两块相同的等腰直角三角板按图2的方式放置，ADAOB＝α，试探究图中两个

带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．

图2

海淀区初二期末数学(三)
2015-2016学年北京市海淀区初二上学期期末数学试卷(含答案)

海淀区八年级第一学期期末练习

数 学 2016.1

一、选择题（本题共36分，每小题3分）

在下列各题的四个备选答案中，只有一个符合题意．请将正确选项前的字母填在表格中相应的位．．置．

1．下列标志是轴对称图形的是

A B C D

002 5用科学记数法表示为

A．2.5106 B．0.25106 C．25106 D．2.5106

2

3．使分式有意义的x的取值范围是

x3 A．x3 B．x3 C．x3 D．x3 4．下列计算中，正确的是

A．(a2)3a8 B．a8a4a2 C．a3a2a5 D．a2a3a5 5．如图，△ABC≌△DCB，若AC＝7，BE＝5，则DE的长为 A．2 B．3 C．4 D

．

5

6．在平面直角坐标系中，已知点A（2，m）和点B（n，－3）关 于x轴对称，则mn的值是

A．－1 B．1 C．5 D．－5

7．工人师傅常用角尺平分一个任意角．做法如下：如图，∠AOB是一个任意角，在边OA，OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度．．分别与点M，N重合，过角尺顶点C作射线OC．由此作法便可得△MOC≌△NOC，其依据是

A．SSS B．SAS C．ASA D．AAS

2．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，2.5微米等于0.000 002 5米，把数字0.000

8．下列各式中，计算正确的是

x31

2

x9x3

22

C．(a2)a4 D． (x2)(x3)x2x6

A．x(2x1)2x21 B．

9．若ab1，则a2b22b的值为

A．4 B．3 C．1 D．0

10．如图，在△ABC中，AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于

D点，则∠DBC的度数是

A．20° B．30° C．40° D．50° 11．若分式

6

的值为正整数，则整数a的值有 a1

A．3个 B．4个 C．6个 D．8个 12．如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的

垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边 的中点，点M为线段EF上一动点，则△CDM周长的最小值为 A．6 B．8

C．10 D．12

二、填空题（本题共24分，每小题3分） 13．当xx

值为0． x1

14．分解因式：x2y4y x

15．计算：3

3y

2

16．如果等腰三角形的两边长分别为3和7，那么它的周长为．

17．如图，DE⊥AB，∠A＝25°，∠D＝45°，则∠ACB的度数为

18．等式(ab)2a2b2成立的条件为

19．如图，在△ABC中，BD是边AC上的高，CE平分∠ACB，交BD于点E，

DE＝2，BC＝5，则△BCE的面积为．

20．图1是用绳索织成的一片网的一部分，小明探索这片网的结点数（V），网眼数（F），边数（E）

之间的关系，他采用由特殊到一般的方法进行探索，列表如下：

表中“☆”处应填的数字为 ；根据上述探索过程，可以猜想V ，F， E之间满足的等量关系为 ；

如图2，若网眼形状为六边形，则V ，F， E之间满足的等量关系为 ．

图1 图2

三、解答题（本题共16分，每小题4分） 1

21(π3)3．

2

1

22．如图，E为BC上一点，AC∥BD，AC＝BE，BC＝DB．

求证：AB= ED．

2x23x423．计算：2． 2

x1x1x2x1

24．解方程：

x3

． 1

x1x1

四、解答题（本题共13分，第25题4分，第26题5分，第27题4分） 25．已知xy3，求[(xy)2(xy)(xy)]2x的值．

26．北京时间2015年7月31日，国际奥委会主席巴赫宣布：中国北京获得2022年第24届冬季奥林

匹克运动会举办权．北京也创造历史，成为第一个既举办过夏奥会又举办冬奥会的城市，张家口也成为本届冬奥会的协办城市．近期，新建北京至张家口铁路可行性研究报告已经获得国家发改委批复，同意新建北京至张家口铁路，铁路全长约180千米．按照设计，京张高铁列车的平均行驶速度是普通快车的1.5倍，用时比普通快车用时少了20分钟，求高铁列车的平均行驶速度．

27．已知：如图，线段AB和射线BM交于点B．

（1）利用尺规完成以下作图，并保留作图痕迹（不写作法）．

①在射线BM上作一点C，使AC＝AB； ②作∠ABM的角平分线交AC于D点；

③在射线CM上作一点E，使CE＝CD，连接DE．

（2）在（1）所作的图形中，猜想线段BD与DE的数量关系，并证明．

A

B

M

海淀区初二期末数学(四)
2014-2015学年北京市海淀区八年级下学期期末考试数学试卷(含答案)

海淀区八年级2014-2015学年第二学期期末练习

数 学

（分数：100分 时间：90分钟） 2015.7

学校 班级 姓名 成绩

一、选择题：（本题共30分，每小题3分）

在下列各题的四个备选答案中，只有一个是正确的． ．．．．

1．一元二次方程3x24x50的二次项系数、一次项系数、常数项分别是

A．3,4,5 B．3,4,5 C．3,4,5 D．3,4,5

2

．函数yx的取值范围是

D．x3 A．x3 B．x3 C．x3

3．下列各曲线表示的y与x的关系中，y不是．．x的函数的是

A．

B． C． D．

4．已知P1（3，y1），P2（2，y2）是一次函数y2x1图象上的两个点，则y1，y2的大小关系是

A．y1y2 B．y1y2 C．y1y2 D．不能确定

25．用配方法解方程x4x70时，原方程应变形为

A．x211 B．x211 C． x423 D．x423

2222

6．本市5月份某一周每天的最高气温统计如下表：则这组数据的中位数和平均数分别是

A．24，25 B．25，26 C．26，24 D．26，25

7．如图，在四边形ABCD中，对角线ACBD， 点E、F、G、H

分别为AB、BC、CD、DA的中点.若AC8，BD6，则四边形

EFGH的面积为

A．14 B．12 C． 24 D． 48

8．如图，在菱形ABCD中，点M、N分别在AB、CD上， AM=CN，

MN与AC交于点O，连接BO．若∠DAC=28°，则∠OBC为

A．28° B．52° C．62° D．72°【海淀区初二期末数学】

9．如图，直线y1xm与y2kxn相交于点A.若点A的横坐

标为2，则下列结论中错误的是 ．．

A．k0 B．m【海淀区初二期末数学】

n

C．当

x

2时，y2y1 D．2knm2

10．如图，若点P为函数ykxb(4x4)图象上的一动点，

m表示点P到原点O的距离，则下列图象中，能表示m与点P的横

坐标x的函数关系的图象大致是

A． B． C． D．

二、填空题：（本题共18分，每小题3分）

11．在□ABCD中，若∠B=50°，则∠C°．

12．将直线y2x3向上平移4个单位长度得到的直线的解析式为．

213．若关于x的方程9x6xm0有两个相等的实数根，则m

14．某通讯公司的4G上网套餐每月上网费用y (单位：元)

与上网流量x（单位：兆）的函数关系的图象如图所示.若

该公司用户月上网流量超过500兆以后，每兆流量的费用为

0.29元，则图中a的值为

15．用两个全等的直角三角形无缝隙不重叠地拼下列图形：

①矩形；②菱形；③正方形；④等腰三角形；⑤等边三角形，一定能够拼成的图形是 ．．

（填序号）.

16．边长为a的菱形是由边长为a的正方形 “形变”得到的，若这个菱形一组对边之间的 距离为h，则称a为这个菱形的“形变度”． h

（1）一个“形变度”为3的菱形与其“形变”前的正方形的面积

之比为 ；

（2）如图，A、B、C为菱形网格（每个小菱形的边长为1， 9“形变度”为）中的格点，则△ABC的面积为 ． 8

三、解答题：（本题共22分，第17题4分，第18题8分，第19题5分，第20题5分）

17

．计算：解：

18．（1）解方程：x(x1)22x．

解：

（2）若x1是方程x24mx2m20的一个根，求代数式3m11的值． 解：

19．如图，E、F是□ABCD对角线AC上的两点，AF=CE.

求证：BE=DF．

证明：

20．在平面直角坐标系xOy中，一次函数的图象经过点A（1，-3）和B（2，0）．

（1）求这个一次函数的解析式；

2

（2）若以O、A、B、C为顶点的四边形为菱形，则点C的坐标为 （直接写出答案）． 解：

四、解答题：（本题共10分，第21题5分，第22题5分）

21. 如图，菱形ABCD的对角线AC、BD相交于点O，DE∥AC，DE=

CE.若AB=2，ABC60，求AE的长.

解：

22．列方程解应用题：

随着经济的增长和人民生活水平的提高，我国公民出境旅游人数逐年上升．据统计，

1AC，连接AE、2

海淀区初二期末数学(五)
2013-2014学年北京市海淀区初二上学期期末数学试卷(含答案)

海淀区2013—2014学年第一学期期末初二数学统一测试 2014.1

一、选择题（本题共30分，每小题3分） 1．下列交通标志是轴对称图形的是（ ）

{ SHAPE \* MERGEFORMAT |

A． B． C． D． 2．下列运算中正确的是（ ）

A． B． C． D． 3．下列长度的三条线段能组成直角三角形的是（ ）

A．1，2，3 B． 2，3，4 C． 3，4，5 D．4，5，6 4．下列二次根式中，是最简二次根式的是（ ）

A． B． C． D． 5．在平面直角坐标系中，点（2，1）关于y轴对称的点的坐标是（ ） A． （－2 ，1 ） B． （ 2 ，1 ） C． （－2 ，－1） D． （2 ，－1）

6．已知图中的两个三角形全等，则∠1等于（ ） A． 72° B． 60° C． 50° D． 58° c7．若分式 的值为0，则x的值为（ ）

A．1 B．－1 C．0 D． 8．已知等腰三角形的一边长为4，另一边长为8，则它的周长是（ ）

A． 12 B． 16 C． 20 D． 16或20 9．从边长为a的大正方形纸板中挖去一个边长为形后，将其裁成四个相同的等腰梯形（如图(1)），一个平行四边形（如图(2)），那么通过计算两个图分的面积，可以验证成立的公式为（ ） A． B． C． D．

10.如图(1)是长方形纸带，，将纸带沿折叠成图(2)，再沿折叠成图(3)， 则图(3)中的的度数是（ ）

b

b的小正方然后拼成形阴影部

图（1） 图（2）

D

AEB

F

DC

AE

F

B

G

D

AE

C

C

B

G

F

图(1) 图(2) 图(3)

A． B． C． D． 二、填空题（本题共18分，每小题3分）

11．若有意义，则x的取值范围是． 12．分解因式： 13．计算： 14．若实数、满足，则．

15．如图，等边△ABC中，AB = 2, AD平分∠BAC交BC于D,

则线段AD的长为 ．【海淀区初二期末数学】

16．下面是一个按某种规律排列的数阵：

A

BDC

1 第1行 2 第2行 3 第3行 4 第4行

根据数阵排列的规律，第5行从左向右数第3个数是第个数是 （用含n的代数式表示）．

三、解答题（本题共19分，第20题4分，其余每小题5分） 17．计算：

18．如图,在△ABC中，AB=AC, D是BC的中点，DE⊥AB于E，DF⊥AC于F．求证：DE=DF．

B

19．已知，求代数式的值．

20．如图，电信部门要在公路m,n之间的S区域修建一座电视信号发射塔P．按照设计要求,发射塔P到区域S内的两个城镇A,B的距离必须相等,到两条公路m，n的距离也必须相等．发射塔P建在什么位置?在图中用尺规作图的方法作出它的位置并标出(不写作法但保留作图痕迹) ．

四、解答题（本题共20分，每小题5分） 21．解方程：

22．先化简，再求值：，其中．

23．小明是学校图书馆A书库的志愿者，小伟是学校图书馆B书库的志愿者，他们各自负责本书库读者当

天还回图书的整理工作．已知某天图书馆A书库恰有120册图书需整理， 而B书库恰有80册图书需整理，小明每小时整理图书的数量是小伟每小时整理图书数量的1.2倍，他们同时开始工作，结果小伟比小明提前15 分钟完成工作．求小明和小伟每小时分别可以整理多少册图书？

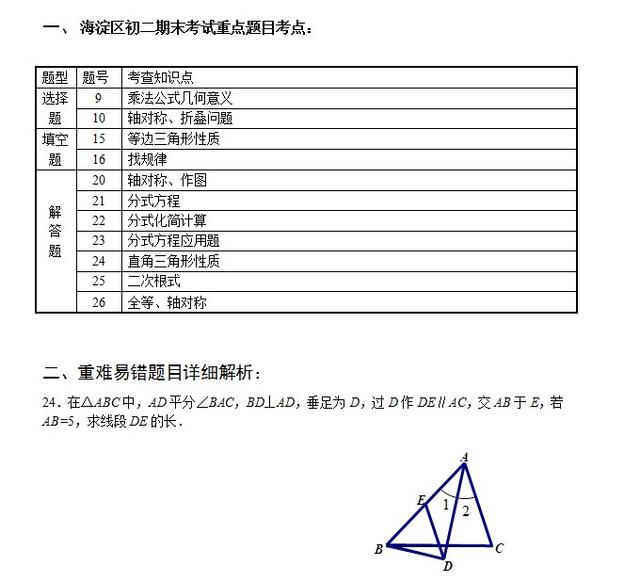
24．在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AC，交AB于E，若AB=5，求线段DE的长．

五、解答题（本题共13分，第25题6分，第26题7分） 25． 阅读材料1：

对于两个正实数，由于，所以，即，所以得到，并且当时，． 阅读材料2：

若，则，因为，所以由阅读材料1可得，，即的最小值是2，只有时，即时取得最小值． 根据以上阅读材料，请回答以下问题： （1）比较大小：

（2）已知代数式变形为，求常数n的值；

（3）当 时，有最小值，最小值为 . （直接写出答案） 26．在四边形ABDE中，C是BD边的中点．

E（1）如图(1)，若AC平分，=90°, 则线段AE、AB、DE的长A

度满足的数量关系为

；（直接写出答案）

BDC

图（1）

（2）如图（2），AC平分， EC平分，

若，则线段AB、BD、DE、AE的长度满足怎样的数量关系？写出结论并证明；

（3）如图（3），BD = 8，AB=2，DE=8，，则线段AE长度的最大值是____________（直接写出答案）．

海淀区八年级第一学期期末练习 数学参考答案及评分标准 2014.1

一、选择题（本题共30分，每小题3分）

三、解答题（本题共19分，第20题4分，其余每小题5分） 17．解：原式=----------------------------------4分

= ------------------------------------5分

18．解法一： ∵D是BC的中点，∴BD=CD . ------------------------------1分 ∵DE⊥AB于E，DF⊥AC于F，

∴∠BED=∠CFD=90° . ---------------------------------------2分 ∵AB=AC，∴ ∠B=∠C . ---------------------------------------3分

B ∵ △BED和△CFD中

∴△BED≌△CFD. ------------------------------------------------4分 ∴

DE=DF. ----------------------------------------------------------5分

解法二： 连接AD .∵在△ABC中， AB=

AC，D是BC的中点，

∴AD平分∠BAC. --------------------------------------------------3分 ∵DE⊥AB于E，DF⊥AC于F，

∴DE=DF. ----------------------------------------------------------5分

19．解：原式==

=------------------------------------------------------------------------------3分 ∵，∴

∴原式=．----------------------------------------------------------5分

20．作图痕迹：

线段AB的垂直平分线的作图痕迹2分

覆盖区域S的直线m与n的夹角的角平分线作图痕迹2分． （未标出点P扣一分）

本文来源：http://www.guakaob.com/chuzhong/521626.html