2016初二下北京朝阳期末考,数学答案

【www.guakaob.com--初二】

2016初二下北京朝阳期末考,数学答案(一)
北京市朝阳区2015-2016学年八年级下期末考试数学试卷含答案

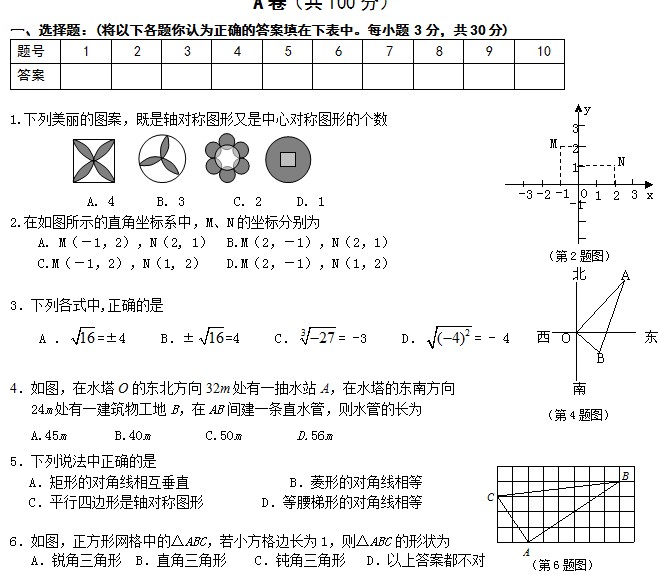
北京市朝阳区2015～2016学年度第二学期期末检测 八年级数学试卷（选用） 2016.7

一、选择题（共30分，每小题3分）

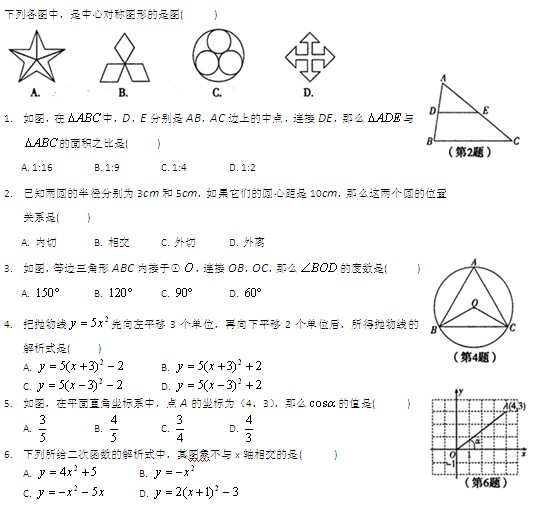
以下每个题中，只有一个选项是符合题意的. 1．下列图形中，是中心对称图形的是

A

B

C D 2．下列二次根式中，最简二次根式是 A B C D． 3．以下列各组数为边长，能构成直角三角形的是 A．2，3，4 B．3，4，6 C．5，12，13 D．6，7，11

4．已知关于x的一元二次方程x23xk0有实数根，则下列四个数中，满足条件的k值为

A．2 B．3 C．4 D．5 5. 如图，□ABCD中，AB=3，BC=5，AE平分∠BAD交BC于点E，则CE的长为

A．1 B．2 C．3 D．4 6． 某市一周的日最高气温如右图所示：

则该市这周的日最高气温的众数是 A. 25 B. 26 C. 27 D. 28

7. 用配方法解方程x2+6x+1=0时，原方程应变形为

A . (x+3)2 = 2 B. (x3)2 = 2

C . (x3)2 = 8 D. (x3)2 = 8

8.如图，菱形ABCD的一边中点M到对角线交点O的距离为5cm，则菱形ABCD的周长为

A．5 cm B．10 cm C．20 cm D．40 cm

9. 已知关于x的一元二次方程xxm10的一个根是0，则m的值为

2

2

A．1 B．0 C．1 D．1或1

10.一个寻宝游戏的寻宝通道由正方形ABCD的边组成，如图1所示.为记录寻宝者的行进路线，在

AB的中点M处放置了一台定位仪器，设寻宝者行进的时间为x，寻宝者与定位仪器之间的距离为y，若寻宝者匀速行进，且表示y与x的函数关系的图象大致如图2所示，则寻宝者的行进路线可能为

A．A→B B．B→C

C．

C→D D．D→A

图1 图2

二、填空题（共18分, 每小题3分） 11．函数y

x的取值范围是

12．如图，直线ykxb(k0)与x轴交于点(－4，0)，则关于x

kxb0的解为x

．

13．下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差：

根据表中数据，要从甲、乙、丙、丁中选择一名成绩好又发挥稳定的运动员参加决赛，应该选择 ．

y2x1图象上的两个点， 14．已知P1（3，y1）、P2（2，y2）是一次函数

则y1y2（填“＞”、“＜”或“=”）．

15．《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题：“直田积八百六十四步，之云阔

不及长一十二步，问阔及长各几步？”译文：“一个矩形田地的面积等于864平方步，且它的宽比长少12步，问长与宽各是多少步？”若设矩形田地的长为x步， 则可列方程为 16. 阅读下面材料：

在数学课上，老师提出如下问题：

老师说：“小敏的作法正确．”

请回答：小敏的作法正确的理由是 ．

三、解答题（共52分， 第17-21题每题4分，第22-25题每题5分，第26-27题每题6分）

17．计算：

18.解方程：x4x30.

19．已知：如图，E、F分别为□ABCD 的边BC、AD上的点，且12． 求证：AE=CF．

D

1

B E

20. 如图，在平面直角坐标系xOy中，已知点B（3，4），BA⊥x轴于A．

（1）画出将△OAB绕原点O逆时针旋转90°后所得的的△OA1B1，并写出点B的对应点B1的坐标为 ；

（2）在（1）的条件下，连接BB1，则线段BB1的长度为 ．

21.直线y=2x-2与x轴交于点A，与y轴交于点B. （1）求点A、B的坐标；

（2）点C在x轴上，且SABC3SAOB,直接写出点C坐

标.

22. 阅读对人成长的影响是巨大的，一本好书往往能改变人的一生，每年的4月23日被联合国教科

2

文组织确定为“世界读书日”．某校本学年开展了读书活动，在这次活动中，八年级（1）班40名学

根据表中的数据，求：

(1)该班学生读书册数的平均数； (2)该班学生读书册数的中位数.

23. 世界上大部分国家都使用摄氏温度（℃），但美国、英国等国家的天气预报使用华氏温度（℉）．两

已知华氏温度y（℉）是摄氏温度x（℃）的一次函数． (1)求该一次函数的表达式；

(2)当华氏温度4℉时，求其所对应的摄氏温度．

24. 如图，矩形ABCD的对角线AC、BD交于点O，且DE∥AC，CE∥BD． （1）求证：四边形OCED是菱形；

（2）若∠BAC＝30°，AC＝4，求菱形OCED的面积．

25. 问题：探究函数yx2的图象与性质．

小华根据学习函数的经验，对函数yx2的图象与性质进行了探究． 下面是小华的探究过程，请补充完整：

（1）在函数yx2中，自变量x可以是任意实数； （2

①m②若A（n，8），B（10，8）为该函数图象上不同的两点，则n ;

（3）如下图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的

点，画出该函数的图象；

根据函数图象可得：

①该函数的最小值为 ；

②已知直线y1

11

x与函数yx2的图象交于C、D两点，当y1y时x的取值范22

围是 .

26.定义：对于线段MN和点P，当PM=PN，且∠MPN≤120°时，称点P为线段MN的“等距点”.特别地，当PM=PN，且∠MPN=120°时，称点P为线段MN的“强等距点”. 如图1，在平面直角坐标系xOy中，点A

的坐标为.

(1)若点B是线段OA的“强等距点”，且在第一象限，则点B的坐标为（，）； (2)若点C是线段OA的“等距点”，则点C的纵坐标t的取值范围是

(3)将射线OA绕点O顺时针旋转30°得到射线l，如图2所示．已知点D在射线l上，点E在第四象限内，且点E既是线段OA的“等距点”，又是线段OD的“强等距点”，求点D坐标.

27.在等腰直角三角形ABC中，∠ACB=90°，AC =BC，直线l过点C且与AB平行．点D在直线l上（不与点C重合），作射线DA．将射线DA绕点D顺时针旋转90°，与直线BC交于点E． （1）如图1，若点E在BC的延长线上，请直接写出线段AD、DE 之间的数量关系； （2）依题意补全图2，并证明此时（1）中的结论仍然成立； （3）若AC=3，CD

=CE的长．

北京市朝阳区2015～2016学年度八年级第二学期期末检测

2016初二下北京朝阳期末考,数学答案(二)
北京市朝阳区2015-2016学年第二学期八年级数学试卷参考答案及评分标准

北京市朝阳区2015～2016学年度八年级第二学期期末检测

八年级数学试卷参考答案及评分标准

2016.7 一、选择题（共30分,每小题3分）

二、填空题（共18分，每小题3分） 11. x3 14. 

16. 对角线互相平分的四边形是平行四边形

三、解答题（共52分，第17-21题每题4分，第22-25题每题5分，第26-27题每题6分） 17. 解：原式,

12. -4

13. 丙

15. x(x12)864



18. 解：原方程变形为(x2)21,

.

x21

.

x13,x21

19．证明： ∵四边形ABCD是平行四边形，

∴AD∥BC. ∴∠FCB＝∠2. ∵∠1＝∠2， ∴∠1＝∠FCB. ∴AE∥CF. 又∵AF∥CE ,

∴四边形AECF是平行四边形.

∴AE=CF.

20. 解：（1）如图.

（-4,3）

（2

）

21. 解：（1）令y=0，得x=1，

∴A（1,0）. 令x=0，得y=-2，

∴B（0,-2）.

（2）

C1(4,0)或C（2-2，0) „„„„„„„„„„„„„„„„„„„„„„„4分

22. 解：（1）x

1

(465461071288) 40

=6.3.

∴该班学生平均每人读书6.3本册. （2）这组数据的中位数为6和7的平均数，即 ∴该班学生读书册数的中位数为6.5.【2016初二下北京朝阳期末考,数学答案】

23.解：（1）设一次函数表达式为ykxb(k0).

67

6.5 2

b32,

由题意，得10kb50



解得

x1.8,

b32.

∴一次函数的表达式为y1.8x32.

（2）当y=-4时，代入得-4=1.8x+32，解得x=-20.

∴华氏温度-4℉所对应的摄氏温度是-20℃.

24.（1）证明：

∵CE∥OD，DE∥OC， ∴四边形OCED是平行四边形. ∵矩形ABCD， ∴AC=BD，OC= ∴OC=OD.

∴平行四边形OCED是菱形.

（2）解：在矩形ABCD中，∠ABC=90°，∠BAC=30°，AC＝4，

∴BC=2. ∴

AB=DC= 连接OE，交CD于点F. ∵四边形ABCD为菱形， ∴F为CD中点. ∵O为BD中点， ∴OF=

11AC，OB=BD. 22

1

BC=1. 2

∴OE＝2OF＝2. ∴S菱形OCED

＝

11

OECD2 22

＝

25. （2）① 1.-------------------1分

②－10.--------------------2分 （3）如右图. ------------------3分

①－2. -----------------4分 ②1x3.-------------------5分

26.（1

）

1 .



（2）t1或t1. （3）解：

∵点E是线段OA的“等距点”，EO＝EA, ∴点E在线段OA的垂直平分线上. 设线段OA的垂直平分线交x轴于点F．

∵A，

F0).

∵点E是线段OD的“强等距点”，EO＝ED，且∠OED＝120°, ∴EODEDO30

. ∵点E在第四象限， ∴∠EOA＝60°.

∴在Rt△OEF中， EF＝3

，OE

∴E3).

∴DEOE. 又∵AODEOD30,

∴ED∥OA.

∴D3). 27. （1）AD＝DE.

（2）补全图形，如图2所示.

证明：如图2，过点D直线l的垂线，交AC于点F. ∵△ABC中，∠BCA＝90°，AC＝BC, ∴∠CAB＝∠B＝45°. ∵直线l∥AB，

∴∠DCF＝∠CAB＝45°. ∴∠DCF＝∠DFC＝45°. ∴CD＝FD.

∵∠DFA＝180°－∠DFC＝135°，【2016初二下北京朝阳期末考,数学答案】

∠DCE＝∠DCA＋∠BCA＝135°，

∴∠DCE＝∠DFA.

∵∠1＋∠3＝∠2＋∠3＝90°， ∴∠1＝∠2.

∴△CDE≌△FDA（ASA）. ∴DE＝DA

图

2

（3）CE＝1或7.

说明：各解答题的其他正确解法请参照以上标准给分.

祝各位老师暑假愉快！

2016初二下北京朝阳期末考,数学答案(三)
北京市朝阳区2015-2016学年八年级下期末考试数学试卷含答案

北京市朝阳区2015-2016学年八年级下期末考试数学试卷含答案

一、选择题（共30分，每小题3分）

以下每个题中，只有一个选项是符合题意的.

1．下列图形中，是中心对称图形的是

A

B

C D

2．下列二次根式中，最简二次根式是

A B C D． 3．以下列各组数为边长，能构成直角三角形的是

A．2，3，4 B．3，4，6 C．5，12，13 D．6，7，11

4．已知关于x的一元二次方程x23xk0有实数根，则下列四个数中，满足条件的k值为

A．2 B．3 C．4 D．5

5. 如图，□ABCD中，AB=3，BC=5，AE平分∠BAD交BC于点E，

则CE的长为

A．1 B．2

C．3 D．4

6． 某市一周的日最高气温如右图所示：

则该市这周的日最高气温的众数是

A. 25 B. 26

C. 27 D. 28

7. 用配方法解方程x2+6x+1=0时，原方程应变形为

A . (x+3)2 = 2 B. (x3)2 = 2

C . (x3)2 = 8 D. (x3)2 = 8

8.如图，菱形ABCD的一边中点M到对角线交点O的距离

为5cm，则菱形ABCD的周长为

A．5 cm B．10 cm

C．20 cm D．40 cm

9. 已知关于x的一元二次方程xxm10的一个根是0，则m

的值为

A．1 B．0 C．1 D．1或1

10.一个寻宝游戏的寻宝通道由正方形ABCD的边组成，如图1所示.为记录寻宝者的行进路线，在22

二、填空题（共18分, 每小题3分）

11．函数yAB的中点M处放置了一台定位仪器，设寻宝者行进的时间为x，寻宝者与定位仪器之间的距离为y，若寻宝者匀速行进，且表示y与x的函数关系的图象大致如图2所示，则寻宝者的行进路线可能为 A．A→B B．B→C C．

C→D D．D→A 图1 图2 x的取值范围是 12．如图，直线ykxb(k0)与x轴交于点(－4，0)，则关于x

kxb0的解为x

．

13．下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差：

根据表中数据，要从甲、乙、丙、丁中选择一名成绩好又发挥稳定的运动员参加决赛，应该选择 ．

y2x1图象上的两个点， 14．已知P1（3，y1）、P2（2，y2）是一次函数

则y1y2（填“＞”、“＜”或“=”）．

15．《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题：“直田积八百六十四步，之云阔

不及长一十二步，问阔及长各几步？”译文：“一个矩形田地的面积等于864平方步，且它的宽比长少12步，问长与宽各是多少步？”若设矩形田地的长为x步， 则可列方程为

16. 阅读下面材料：

在数学课上，老师提出如下问题：

请回答：小敏的作法正确的理由是

．

三、解答题（共52分， 第17-21题每题4分，第22-25题每题5分，第26-27题每题6分）

17．计算：

18.解方程：x4x30.

19．已知：如图，E、F分别为□ABCD 的边BC、AD上的点，且12．

求证：AE=CF． D 1B

20. 如图，在平面直角坐标系xOy中，已知点B（3，4），BA⊥x轴于A．

（1）画出将△OAB绕原点O逆时针旋转90°后所得的的△OA1B1，并写出点B的对应点B1的坐标为 ；

（2）在（1）的条件下，连接BB1，则线段BB1的长度为 ．

21.直线y=2x-2与x轴交于点A，与y轴交于点B.

（1）求点A、B的坐标；

（2）点C在x轴上，且SABC3SAOB,直接写出点C坐

标.

22. 阅读对人成长的影响是巨大的，一本好书往往能改变人的一生，每年的4月23日被联合国教科文组织确定为“世界读书日”．某校本学年开展了读书活动，在这次活动中，八年级（1）班40名学生读书册数的情况如下表:

2

2016初二下北京朝阳期末考,数学答案(四)
2015-2016朝阳区初二下期末数学试题

北京市朝阳区2015～2016学年度第二学期期末检测 八年级数学试卷（选用） 2016.7

以下每个题中，只有一个选项是符合题意的. 1．下列图形中，是中心对称图形的是

A B C D 2．下列二次根式中，最简二次根式是 A B C D． 3．以下列各组数为边长，能构成直角三角形的是 A．2，3，4 B．3，4，6 C．5，12，13 D．6，7，11

4．已知关于x的一元二次方程x23xk0有实数根，则下列四个数中，满足条件的k值为 A．2 B．3 C．4 D．5 5. 如图，□ABCD中，AB=3，BC=5，AE平分∠BAD交BC于点E，则CE的长为

A．1 B．2 C．3 D．4 6． 某市一周的日最高气温如右图所示：

则该市这周的日最高气温的众数是

A. 25 B. 26 C. 27 D. 28

7. 用配方法解方程x2+6x+1=0时，原方程应变形为

A . (x+3)2 = 2 B. (x3)2 = 2 C . (x3)2 = 8 D. (x3)2 = 8

8.如图，菱形ABCD的一边中点M到对角线交点O的距离为5cm，则菱形ABCD的周长为

A．5 cm B．10 cm C．20 cm D．40 cm

9. 已知关于x的一元二次方程xxm10的一个根是0，则m的值为

A．1 B．0 C．1 D．1或1

10.一个寻宝游戏的寻宝通道由正方形ABCD的边组成，如图1所示.为记录寻宝者的行进路

线，在AB的中点M处放置了一台定位仪器，设寻宝者行进的时间为x，寻宝者与定位仪器之间的距离为y，若寻宝者匀速行进，且表示y与x的函数关系的图象大致如图2所示，则寻宝者的行进路线可能为 A．A→B B．B→C

C．

C→D D．D→A

图1 图2

二、填空题（共18分, 每小题3分） 11．函数y

22

x的取值范围是

12．如图，直线ykxb(k0)与x轴交于点(－4，0)，则关于x

kxb0的解为x

．

13．下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差：

根据表中数据，要从甲、乙、丙、丁中选择一名成绩好又发挥稳定的运动员参加决赛，应该选择 ．

y2x1图象上的两个点， 14．已知P1（3，y1）、P2（2，y2）是一次函数

则y1y2（填“＞”、“＜”或“=”）．

15．《算学宝鉴》中记载了我国南宋数学家杨辉提出的一个问题：“直田积八百六十四步，之云阔不及长一十二步，问阔及长各几步？”译文：“一个矩形田地的面积等于864平方步，且它的宽比长少12步，问长与宽各是多少步？”若设矩形田地的长为x步， 则可列方程为 16. 阅读下面材料：

在数学课上，老师提出如下问题：

老师说：“小敏的作法正确．”

请回答：小敏的作法正确的理由是 ．

三、解答题（共52分， 第17-21题每题4分，第22-25题每题5分，第26-27题每题6分）

17．计算：

18.解方程：x4x30.

19．已知：如图，E、F分别为□ABCD 的边BC、AD上的点，且12． 求证：AE=CF．

D

B

20. 如图，在平面直角坐标系xOy中，已知点B（3，4），BA⊥x轴于A．

（1）画出将△OAB绕原点O逆时针旋转90°后所得的的△OA1B1，并写出点B的对应点B1的坐标为 ；

（2）在（1）的条件下，连接BB1，则线段BB1的长度为 ．

21.直线y=2x-2与x轴交于点A，与y轴交于点B. （1）求点A、B的坐标；

（2）点C在x轴上，且SABC3SAOB,直接写出点C坐标.

2

22. 阅读对人成长的影响是巨大的，一本好书往往能改变人的一生，每年的4月23日被联合国教科文组织确定为“世界读书日”．某校本学年开展了读书活动，在这次活动中，八年级（1）班40名学生读书册数的情况如下表:

(1)该班学生读书册数的平均数； (2)该班学生读书册数的中位数.

23. 世界上大部分国家都使用摄氏温度（℃），但美国、英国等国家的天气预报使用华氏温度（℉）．两种计量之间有如下对应：

已知华氏温度y（℉）是摄氏温度x（℃）的一次函数． (1)求该一次函数的表达式；

(2)当华氏温度4℉时，求其所对应的摄氏温度．

24. 如图，矩形ABCD的对角线AC、BD交于点O，且DE∥AC，CE∥BD． （1）求证：四边形OCED是菱形；

（2）若∠BAC＝30°，AC＝4，求菱形OCED的面积．【2016初二下北京朝阳期末考,数学答案】

25. 问题：探究函数yx2的图象与性质．

小华根据学习函数的经验，对函数yx2的图象与性质进行了探究． 下面是小华的探究过程，请补充完整：

（1）在函数yx2中，自变量x可以是任意实数； （2）下表是y与x的几组对应值．

①m= ；

②若A（n，8），B（10，8）为该函数图象上不同的两点，则n ;

（3）如下图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根

据描出的点，画出该函数的图象；

根据函数图象可得：

①该函数的最小值为 ； ②已知直线y1

11

x与函数yx2的图象交于C、D两点，当y1y时x22

的取值范围是 .

26.定义：对于线段MN和点P，当PM=PN，且∠MPN≤120°时，称点P为线段MN的“等距点”.特别地，当PM=PN，且∠MPN=120°时，称点P为线段MN的“强等距点”. 如图1，在平面直角坐标系xOy中，点A

的坐标为.

(1)若点B是线段OA的“强等距点”，且在第一象限，则点B的坐标为（）； (2)若点C是线段OA的“等距点”，则点C的纵坐标t的取值范围是； (3)将射线OA绕点O顺时针旋转30°得到射线l，如图2所示．已知点D在射线l上，点E在第四象限内，且点E既是线段OA的“等距点”，又是线段OD的“强等距点”，求点D坐标.

27.在等腰直角三角形ABC中，∠ACB=90°，AC =BC，直线l过点C且与AB平行．点D在直线l上（不与点C重合），作射线DA．将射线DA绕点D顺时针旋转90°，与直线BC交于点E．

（1）如图1，若点E在BC的延长线上，请直接写出线段AD、DE 之间的数量关系； （2）依题意补全图2，并证明此时（1）中的结论仍然成立； （3）若AC=3，CD

=CE的长．

2016初二下北京朝阳期末考,数学答案(五)
2015-2016学年北京市朝阳区八年级上学期期末练习数学试题(含答案)

北京市朝阳区2015— 2016学年度第一学期八年级数学期末试卷2016.1

一、选择题（每小题3分，共30分）

1．下列图形中，是轴对称图形的是（ ）

2．某种流感病毒的直径在0.00 000 012米左右，将0.00 000 012用科学记数法表示应为（ ）A．0.12×10-6 B．12×10-8 C．1.2×10-6 D．1.2×10-7 3．下列长度的三根木棒能组成三角形的是（ ） A．3，4，8 B．4，4，8 C．5，6，10 D．6，7，14 4．点(2，3)关于y轴对称的点的坐标是（ ）

A．（2，3） B．（2，3） C.（2，3）D.（3，2） 5. 如图，在Rt△ABC中，∠C=90°，∠CAB的平分线AD交BC于点D，DE⊥AB于点E，若CD=4， 则DE的长为（ ）

A．2 B．3 C．4 D．5 6． 下列计算正确的是（ ）

A．x

2

x3x5 B．x2+x3=2x5 C．2x-3x=-1 D．(2x)3=2x3

7.将一副三角尺按如图方式进行摆放，则∠1的度数为（ ） A. 60° B. 90° C. 120° D. 135°

8.下列各式中,从左到右的变形是因式分解的是（ ）

2

A. 4x1(2x1)(2x1) B. a(xy1)axaya

C. (x3y)(x3y)x9y D. acab1a(cb)1

22222

9.如图1，某温室屋顶结构外框为△ABC，立柱AD垂直平分横梁BC，∠B=30°，斜梁AC=4m.为增大向阳面的面积，将立柱增高并改变位置，使屋顶结构外框变为△EBC（点E在BA的延长线上），立柱EF⊥BC，如图2所示，若EF=3m，.则斜梁增加部分AE的长为（ ） A.0.5m B. 1m C. 1.5m D. 2m

图1 图2

10．如图，在△ABC中，∠C=40°，将△ABC沿着直线l折叠，点C落在点D的位置，则∠1－∠2的度数是（ ） A. 40° B. 80° C. 90° D. 140°

1

二、填空题（每小题3分，共18分） 11．若分式

1

有意义，则x的取值范围是 ． x3

6x2y

12．计算：．

yx

13．分解因式：5a2-10ab+5b2=．

14. 如图，AB＝AC，点D，E分别在AB，AC上，CD，BE交于点F，只添加一个条件使△ABE≌△ACD， 添加的条件是:______________．

15．等腰三角形的一个内角为30°，则该等腰三角形的顶角的度数为____________． ．．

16. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角” (如图所示)就是一例

.

这个三角形的构造法则为：两腰上的数都是1，其余每个数均为其上方左右两数之和.事实上，这个三角形给出了ab（n为正整数）的展开式（按a的次数由大到小的顺序排列）的系数规律.例如，在三角形中第三行的三个数1，2，1，恰好对应aba22abb2展开式中各项的系数;第四行的四个数1，3，3，1，恰好对应着aba33a2b3ab2b3展开式中各项的系数等等.根据上面的规律，ab的展开式中各项系数最大的数为 ；

式子7557451073510725575+5的值为

2

2

3

4

5

3

4

2

n

三、解答题（17题3分，18-19题每小题4分，20-26题每小题5分，27题6分，共52分） 17．如图，点D在△ABC的BC边的延长线上，且∠A=∠B.

（1）尺规作图：作∠ACD的平分线CE（保留作图痕迹，不要求写作法）；

（2）在（1）的条件下，射线CE与线段AB的位置关系是（不要求证明）.

121

18.

计算：(3)0()1． 19.计算：． -2

4a-2a-2a

20.已知：如图，点D在△ABC的BC边上，AC∥BE，BC=BE，∠ABC=∠E，求证：AB=DE．

21. 一个多边形的内角和是它的外角和的3倍，求这个多边形的边数．

3

22.解分式方程：

x3-=1.

x-1(x-1)(x+2)

2

23.已知xx5，求(2x1)x(52x)+2x2x的值．

2

24.中华优秀传统文化积淀着中华民族最深层的精神追求和价值取向，特别是其中蕴含的丰富深厚的道德理念，为一代又一代中华儿女提供了精神归依和心灵居所，成为涵养社会主义核心价值观的重要源泉.为了培育和践行社会主义核心价值观，大力弘扬中华优秀传统文化,某校决定为各班购进《三国演义》和《水浒传》连环画若干套,其中每套《三国演义》连环画的价格是每套《水浒传》连环画价格的1.5倍，用3600元购买《水浒传》连环画的套数比用相同的钱数购买《三国演义》连环画的套数多10套.求每套《水浒传》连环画的价格.

25.如图，在△ABC中，AB=AC，其中AD，BE都是△ABC的高．求证：∠BAD=∠CAD=∠EBC．

4

26．阅读下面材料：

一个含有多个字母的式子中，如果任意交换两个字母的位置，式子的值都不变，这样的式子就叫做对称式.

L 例如：a+b+c，abc，a2+b2，

含有两个字母a，b的对称式的基本对称式是a+b和ab，像a2+b2，(a+2)(b+2) 等对称式都可以用a+b，ab表示，例如：a2+b2=(a+b)2-2ab.

请根据以上材料解决下列问题： （1）式子① a2b2 ②a2-b2 ③

11

+中，属于对称式的是_________(填序号)； ab

（2）已知(x+a)(x+b)=x2+mx+n .

1ba

，求对称式+的值； 2ab

a4+1b4+1

+②若n=-4，直接写出对称式的最小值. a2b2

①若m=-2,n=

5

本文来源：http://www.guakaob.com/chuzhong/523574.html