初一数学因式分解阴影期末题

【www.guakaob.com--初一】

初一数学因式分解阴影期末题(一)
2015学年七年级期末数学复习卷6----因式分解

2015学年七年级期末数学复习卷6----因式分解

姓名班级

一、填空题：（每空2分，第10题3分共31分） 1、 把下列各式的公因式写在横线上：

（1）5x225x2y、； （2）4x2n6x4n、。 2、 直接写出因式分解的结果： （1）x2y2y23、 如果xy0,

；（2）3a26a3

。

xy7,则x2yxy2

2

，x2y2

。

。

(x3)是二次三项式xkx15的因式，那么k4、 若(x5)、

2

5、 若a2b2b10，则a

，b＝。

6、 在一边长为32.75cm的正方形中，挖去一个边长为27.25cm的正方形，则剩下的面积 是 cm2。

7、 若abc0，则abc2ac。 8、 已知矩形的面积是x2x35

22

2

2

(x7)，其中一边长是x7，则表示矩形的另一边

的代数式是 。

9、出两个整式P、Q，使PQ=(aba)b1，则；。 10、多项式4x2+1加上一个单项式后，使它成为一个整式的完全平方，则加上的单项式可以是 、 、 。（填上三个你认为正确的即可） 二、选择题：（每小题3分，共24分）

1、下列各式从左到右的变形中，是因式分解的为（ A、x(ab)axbx

2

2

）

2

B、x1y(x1)(x1)y

D、axbxcx(ab)c

C、x22xyy2(xy)2

2、一个多项式分解因式的结果是(b32)(2b3)，那么这个多项式是（ A、b4

6

）

B、4b

6

C、b4

6

D、b4

）

6

3、将x2xy3y3x分解因式，下列分组方法不当的是（ A、(x23x)(3yxy) C、(xxy3x)3y

2

B、(x2xy)(3y3x) D、(xxy)(3x3y)

）

2

2

2

4、下列多项式中，含有因式(y1)的多项式是（ A、y2xy3x

2

2

2

2

B、(y1)(y1) D、(y1)2(y1)1

2

C、(y1)(y1)

2

5、使代数式xax20在整数范围内可以因式分解的a的取值有（ ）个 A、3 B、4 C、6 D、8

6、已知多项式2xbxc分解因式为2(x3)(x1)，则b,c的值为（ A、b3,c1

B、b6,c2

C、b6,c4

2

）

D、b4,c6

n

7、若将(2x)81分解后得(4x29)(2x3)(2x3)，那么n的值为 （ ） A、2 B、6 C、4 D、8

8、在边长为a的正方形中挖掉一个边长为b的小正方形（a>b）。把余下的部分剪拼成一个矩形（如图）。通过计算图形（阴影部分）的面积，验证了一个等式，则这个等式是（ A、ab(ab)(ab) B、(ab)a2abb C、(ab)a2abb D、a

aba(ab)

2

2

2

2

2

2

2

2

2

）

三、将下列各式在有理数范围内分解因式【每小题5分，共30分】 （1）6m2n15mn230m2n2

（3）x4

8x2

9

（5）x2

y2

12xy

（2）ab(ab)2a(ba)2ac(ab)2

（4）a2b2

4a4b

（6）(2x23x)(2x2

3x1)2

四、解答题及证明题（5+5+5分，共15分） 1、 已知ab2，ab2，求

2、 已知a、b、c是△ABC的三边的长，且满足a2bc2b(ac)0，试判断此三

角形的形状。

3、 求x2xy2y27的整数解。

2

2

2

131

aba2b2ab3的值。 22

初一数学因式分解阴影期末题(二)
因式分解期末复习

因式分解期末复习

班级____________学号_____________姓名_____________

一、填空题：（每小题2分，共24分）

1、 把下列各式的公因式写在横线上：

①5x25xy、 ②4x

2、 填上适当的式子，使以下等式成立：

（1）2xyxyxyxy(

（2）aann222222n6x4n23x2n ) ) a2nan(

3、 在括号前面填上“＋”或“－”号，使等式成立：

（1）(yx)2(xy)2； （2）(1x)(2x)(x1)(x2)。

4、 直接写出因式分解的结果：

（1）xyy

2222；（2）3a6a32。 5、 若a2b2b10，则a

22，b＝。 6、 若xmx16x4，那么m=________。

7、 如果xy0,

2xy7,则x2yxy22，x2y2。 。 8、 简便计算：7.29－2.71

9、 已知a113，则a22的值是 。 aa

10、如果2a+3b=1,那么3-4a-6b= 。

11、若xmxn是一个完全平方式，则m、n的关系是 。

12、已知正方形的面积是9x6xyy （x>0，y>0）,利用分解因式，写出表示该正方形的边长的代数式 。

二、选择题：（每小题2分，共20分）

1、下列各式从左到右的变形中，是因式分解的为（ ）

A、x(ab)axbx

2222 B、x1y(x1)(x1)y D、axbxcx(ab)c

33222C、x1(x1)(x1) 2、一个多项式分解因式的结果是(b2)(2b)，那么这个多项式是（

A、b4 6） B、4b 6 C、b4 6D、b4 6

3、下列各式是完全平方式的是（

A、x2x） C、xxy1

） D、x2x1 21 42B、1x 2 4、把多项式m(a2)m(2a)分解因式等于（

A (a2)(mm) B (a2)(mm)

C、m(a-2)(m-1)

2222 2 D、m(a-2)(m+1) 25、9(ab)12(ab)4(ab)因式分解的结果是（

A、(5ab) B、(5ab) C、(3a2b)(3a2b)

6、下列多项式中，含有因式(y1)的多项式是（

A、y2xy3x

222222 ） 2D、(5a2b) ）

）

B、(y1)(y1) 222C、(y1)(y1) 7、分解因式x1得（ A、(x1)(x1) 222D、(y1)2(y1)1 4 B、(x1)(x1) D、(x1)(x1)

） 322C、(x1)(x1)(x1) 28、已知多项式2xbxc分解因式为2(x3)(x1)，则b,c的值为（

A、b3,c1 B、b6,c2 C、b6,c4 D、b4,c6

） 9、a、b、c是△ABC的三边，且a2b2c2abacbc，那么△ABC的形状是（

A、直角三角形 B、等腰三角形 C、等腰直角三角形 D、等边三角形

10、在边长为a的正方形中挖掉一个边长为b的小正方形（a>b）。把余下的部分剪拼成一个矩形（如图）。通过计算图形（阴影部分）的面积，验证了一个等式，则这个等式是（

A、ab(ab)(ab)

B、(ab)a2abb

C、(ab)a2abb

D、aaba(ab)

22222

2222 ）

三、将下列各式分解因式【说明：（1）—（4）每小题4分，（5）—（8）每小题5分，共36分】

（1）3x12x

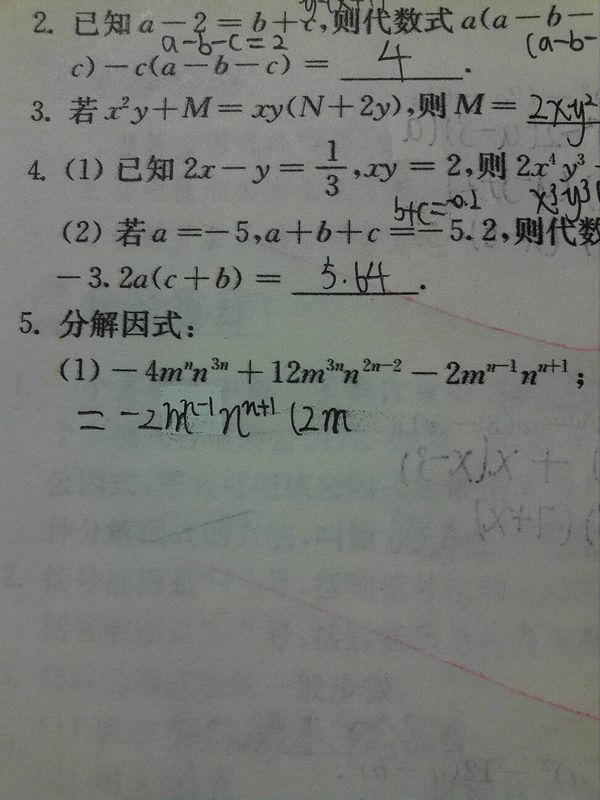
（3）2x22x

（5）20abx45bxy

（7）2m(a-b)-3n(b-a)

四、解答题及证明题（每小题7分，共14分）

1、 已知ab2，ab2，求

2、 利用分解因式证明：255 能被120整除。

712223 （2）2a(x1)2ax 2221 2 （4）ab4a4b 22 （6）xy12xy 22 （8）(ab)(3ab)(a3b)(ba) 22131aba2b2ab3的值。 22

五、大正方形的周长比小正方形的周长长96厘米，它们的面积相差960平方厘米。求这两个正方形的边长。

选作题：已知a、b、c是△ABC的三边的长，且满足a2bc2b(ac)0，试判断此三角形的形状。

1、 已知三个连续奇数的平方和为251，求这三个奇数。

四、附加题（10＇×2=20＇）

1. 阅读下列因式分解的过程，再回答所提出的问题：

1+x+x(x+1)+x(x+1)=(1+x)[1+x+x(x+1)]

=(1+x)(1+x)

=(1+x)

(1)上述分解因式的方法是 ，共应用了 次.

(2)若分解1+x+x(x+1)+x(x+1)+„+ x(x+1)

222004322222，则需应用上述方法 次，结果是 . n(3)分解因式：1+x+x(x+1)+x(x+1)+„+ x(x+1)(n为正整数).

2. 若二次多项式x2kx3k能被 x-1整除，试求k的值。 22

初一数学因式分解阴影期末题(三)
初一数学《因式分解》期末复习教学案

初一数学《因式分解》期末复习教学案

班级 学号 姓名 一、知识点： 1、因式分解： （1） 把一个多项式写成几个整式的积的形式叫做多项式的因式分解。 （2） 多项式的乘法与多项式因式分解的区别 简单地说：乘法是积化和，因式分解是和化积。 ．．．．（3）因式分解的方法：

①提公因式法； ②运用公式法。 2、因式分解的应用：

（1）提公因式法：如果多项式的各项含有公因式，那么就可以把这个公因式提出来。把多项式化成公因式与另一个多项式的积的形式，这种分解因式的方法叫做提公因式法。

（2）公因式：多项式ab＋ac＋ad的各项ab、ac、ad都含有相同的因式a，a称为多项式各项的公因式。

（3）用提公因式法时的注意点： ① 公因式要提尽，考虑的顺序是，先系数，再单独字母，最后多项式。如：

4a2(a-2b)-18ab(a-2b)=2a(a-2b)(2a-9b)； ② 当多项式的第一项的系数为负数时，把“－”号作为公因式的负号写在

2

括号外，使括号内的第一项的系数为正。如：-2m3+8m2-12m= -2m(m-4m+6)； ．③ 提公因式后，另一个多项式的求法是用原多项式除以公因式。 （4）运用公式法的公式： ① 平方差公式：a2-b2=(a+b)(a-b) ② 完全平方公式： a2+2ab+b2=(a+b)2 a2-2ab+b2=(a-b)2 （5）因式分解的步骤和要求：

把一个多项式分解因式时，应先提公因式，注意公因式要提尽，然后．．．．．

再应用公式，如果是二项式考虑用平方差公式，如果是三项式考虑用完全平

方公式，直到把每一个因式都分解到不能再分解为止。 如：

-2x5y+4x3y3-2xy5=-2xy(x4-2x2y2+y4)=-2xy(x2-y2)(x2+y2)=-2xy(x+y)(x-y)(x2+y2) 例一、填空

1、分解因式：4a24a1，aab2， 2、a22abb2、a2b2的公因式是 3、分解因式：(a2b2)24a2b2 4、若x2pxq(x2)(x4)，则p ，q 。 例二、判断

1、4x2yxy3xy2xy(4x3y) （ ）

1

2、m24(m2)2 （ ）

11

3、a2abb2(a2b)2 （ ）

44例三、选择

1、下列从左边到右边的变形，是因式分解的是（ ）

（A）(3x)(3x)9x2 （B）m3n3(mn)(m2mnn2) （C）(y1)(y3)(3y)(y1) （D）4yz2y2zz2y(2zyz)z 2、将多项式6a3b23a2b212a2b3分解因式时，应提取的公因式是（ ）

3ab 3a2b2 3a2b 3a3b3 （A）（B）（C）（D）

2、下列多项式中能用平方差公式分解因式的是（ ）

（A）a2(b)2 （B）5m220mn （C）x2y2 （D）x29 能用完全平方公式分解的是（ ）

（A）a22ax4x2 （B）a24ax4x2 （C）2x14x2 （D）x444x2 3、若(pq)2(qp)3(qp)2E，则E是（ ）

（A）1qp （B）qp （C）1pq （D）1qp 例四、分解因式

1、8a3b212ab3c6a3b2c 2、8a(xa)4b(ax)6c(xa)

3、4x21 4、a2b20.01

5、a28a16；

例五、分解因式，

2

6、(a2b)26(a2b)9；

1

1、a3a 2。3x212 3、x22xy2y2；

2

4、 5、4mn4m2n2．x5y3x3y5 6、4(ab)216(ab)2 7、

9、8ax216axy8ay2 10、(a21)24a2

例六、分解因式

1、9m2n23mn 2、4x2y22y1

3、a24a4c2 4、x2y2axay

例七、用简便方法计算：

（1）20042-4008×2005+20052 （2）9.92－9.9×0.2＋0.01

443100123.71.320.8 （3） （4）22

55520032001

例八、先分解因式，再计算求值．

1

3x2(a3)4x2y(a3)，其中a，x3，y1．

2

3

9216

a2abb2 8、4ab2a2b2b 169

例九、（1）已知x＋y=4，xy=2，求2x3y＋4x2y2＋2xy3的值。

（2）已知：4m+n=90，2m－3n=10，求(m+2n)2－(3m－n)2的值。

（3）已知a2-2a+b2+4b+5=0，求(a+b)2005的值。 当堂检测

一、填空题： 1、2xy2x2yxyxy(

)

2、在括号前面填上“＋”或“－”号，使等式成立： （1）(yx)2

(xy)2； （2）(1x)(2x)(x1)(x2)。

3、直接写出因式分解的结果： （1）x2y2y2

；（2）3a26a3

。

。

4、若a2b22b10，则a

，b＝

5、若x2mx16x42，那么m=________。 6、如果xy0,xy7,则x2yxy27、简便计算：7.292－2.7128、已知a

。

，x2y2 。

11

3，则a22的值是。 aa

9、如果2a+3b=1,那么3-4a-6b= 。 二、选择题：

10、下列各式从左到右的变形中，是因式分解的为（ ）

A、x(ab)axbx

B、x21y2(x1)(x1)y2 D、axbxcx(ab)c

C、x21(x1)(x1)

11、下列各式是完全平方式的是（ ）

1

A、x2x B、1x2 C、xxy1

412、分解因式x41得（

）

D、x22x1

A、(x21)(x21) B、(x1)2(x1)2 C、(x1)(x1)(x21) D(x1)(x1)3

4

13、a、b、c是△ABC的三边，且a2b2c2abacbc，那么△ABC的形状是 A、直角三角形 B、等腰三角形 C、等腰直角三角形 D、等边三角形 14、在边长为a的正方形中挖掉一个边长为b的小正方形（a>b）。把余下的部分剪拼成一个矩形。通过计算图形（阴影部分）的面积，验证了一个等式，则这个等式是（ ）

A、a2b2(ab)(ab) B、(ab)2a22abb2

C、(ab)2a22abb2 D、a2aba(ab) 三、将下列各式分解因式 （1）3x12x3

（4）a2b24a4b

（7）2m(a-b)-3n(b-a)

（9）3a2－9ab （12）x

2

(y2)2y

（15）25x2－16y2；

（2）2a(x21)22ax2 （3）2x22x

1

2

（5）20a2bx45bxy2 （6）x2y212xy （8）(ab)(3ab)2(a3b)2(ba)

10）3x2

6xy3y2 （11）(x24)216x2

13）－5a2＋25a； （14）3a2－9ab；

16）x2＋4xy＋4y2. （17）4x3y＋4x2y2＋xy3； 5

（ （（

初一数学因式分解阴影期末题(四)
七下因式分解期末复习卷]

七下数学因式分解期末复习卷

班级____________学号_____________姓名_____________

一、填空题： 1、

5x225x2y的公因式是 ；

2

2、 填上适当的式子，使等式成立：2xy

x2yxyxy(

)

3、 在括号前面填上“＋”或“－”号，使等式成立： （1）(yx)

2



(xy)2； （2）(1x)(2x)

(x1)(x2)。

4、 直接写出因式分解的结果： （1）x5、 若

2

y2y2

；（2）3a

2

6a3，b＝

。

。

a2b22b10，则a

2

6、 若x

mx16x4

2

，那么m=________。

7、 如果x

y0,xy7,则x2yxy2

2

，x2y2

。

。

8、 利用因式分解简便计算：7.29

－2.712

9、如果2a+3b=1,那么3-4a-6b= 。 10、已知正方形的面积是

9x26xyy2

（x>0，y>0）,利用分解因式，写出表示该正方形的边长的代数

式 。 二、选择题：

1、下列各式从左到右的变形中，是因式分解的为（ A、x(ab)C、x

2

）

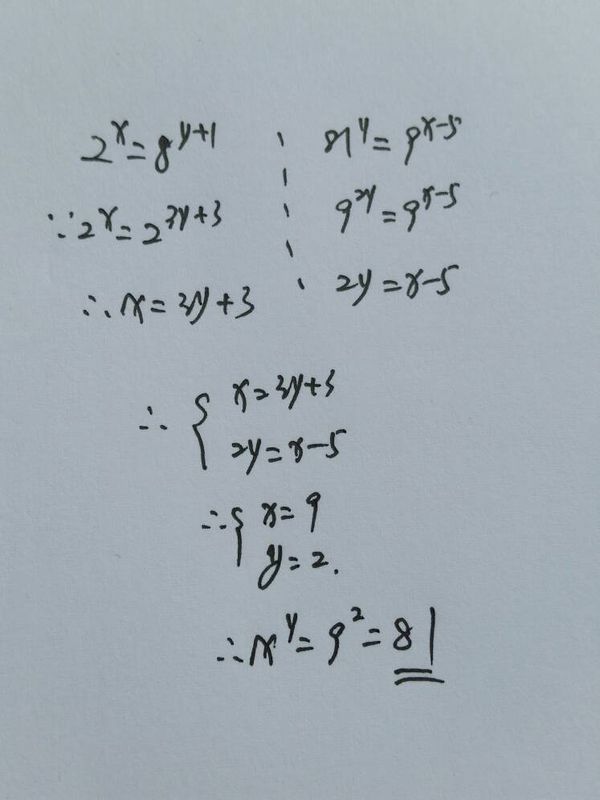
axbx

3

B、x

2

1y2(x1)(x1)y2

x(ab)c

1(x1)(x1) D、axbxc

2、一个多项式分解因式的结果是(bA、b

6

2)(2b3)，那么这个多项式是（ ）

C、b）

C、x

6

4

B、4b

6

4

D、b

6

4【初一数学因式分解阴影期末题】

3、下列各式是完全平方式的是（ A、x

2

x

1

4

2

B、1

x2

xy1

）

D、x

2

2x1

4、把多项式mA (a2)(m

(a2)m(2a)分解因式等于（

2

m) B (a2)(m2m)

D、m(a-2)(m+1)

）

2

C、m(a-2)(m-1) 5、9(ab)

2

12(a2b2)4(ab)2因式分解的结果是（

2

A、 (5ab) B、(5ab)

2

C、(3a2b)(3a2b) D、(5a2b)

6、分解因式xA、(x

2

4

1得（

）

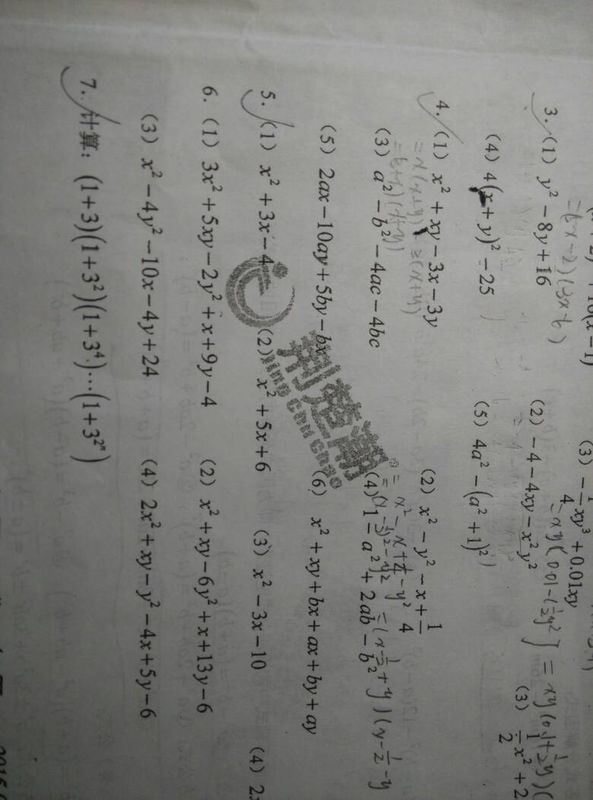
B、(x1)

2

1)(x21)

2

(x1)2【初一数学因式分解阴影期末题】

3

C、(x1)(x1)(x7、已知多项式2xA、b

2

1) D、(x1)(x1)

）

bxc分解因式为2(x3)(x1)，则b,c的值为（

B、b

3,c1 6,c2 C、b6,c4 D、b4,c6

8、在边长为a的正方形中挖掉一个边长为b的小正方形（a>b）。把余下的部分剪拼成一个矩形（如图）。通过计算图形（阴影

部分）的面积，验证了一个等式，则这个等式是（ ）

A、a

2

b2(ab)(ab)

B、(ab)2

a22abb2 C、(ab)2

a22abb2

D、a

2

aba(ab)

三、将下列各式分解因式

（1）x2

y-2xy2

(2)t2

-16 (3)a2

-4a+4 （4）3x12x3

（5）2x

2

2x

1

2

（6）2m(a-b)-3n(b-a)

（7）x2

-2xy+y2

-1 (8)(a2

+b2)2

-4a2b2

（9）a

2

b24a4b

四、已知ab2，ab2，求1a3ba2b21

ab322

的值。

五、计算：（9x3

-x）÷(3x-1)

六、一个正方形的边长增加2厘米，面积增加12平方厘米，求这个正方形的边长.

七、阅读题：

阅读下列因式分解的过程，再回答所提出的问题： 1+x+x(x+1)+x(x+1)2【初一数学因式分解阴影期末题】

=(1+x)[1+x+x(x+1)] =(1+x)2

(1+x) =(1+x)3

(1)上述分解因式的方法是 ，共应用了 次. (2)若分解1+x+x(x+1)+x(x+1)2

+„+ x(x+1)

2004

，则需应用上述方法 次，结果是 .

(3)分解因式：1+x+x(x+1)+x(x+1)2

+„+ x(x+1)n

(n为正整数

).

初一数学因式分解阴影期末题(五)
整式乘法与因式分解复习题 及答案

整式乘法与因式分解复习题 及答案

一、选择题（共10小题；共30分） 1. 下列式子中是完全平方式的是 ( )

A. 7

B. 18

A. a2+ab+b2

B. a2+2a+2

C. a2−2b+b

D. a2+2a+1

2. 下列各式由左边到右边的变形中，属于分解因式的是 ( )

A. a x+y =ax+ay B. x2−4x+4=x x−4 +4 C. 10x2−5x=5x 2x−1

D. x2−16+6x= x+4 x−4 +6x 3. 下列计算正确的是 ( )

A. a3⋅a4=a12 C. a2b 3=a6b3

B. a3 4=a7 D. a3÷a4=a a≠0

4. 在 0，2， −3 0，−5 这四个数中，最大的数是 ( )

A. 0

B. 2

C. −3 0

D. −5

5. 若 2ambm+n 3=8a9b15 成立，那么 ( )

A. m=3 ， n=2

B. m=n=3

43

C. m=6 ， n=2 D. m=3 ， n=5

6. 代数式 3x2−4x+6 的值为 9，则 x2−x+6 的值为 ( )

C. 12

D. 9

7. 若 M 3x−y2 =y4−9x2，那么代数式 M 应是 ( )

A. 3x+y2

B. 3x−y2

C. −3x−y2

D. −3x+y2

8. 把 x2−y2−2y−1 分解因式结果正确的是 ( )

A. x+y+1 x−y−1 C. x+y−1 x+y+1

9. 如果 x−3 x=1，则 x 的取值为 ( )

A. x≥3 C. x=0

B. x=3

D. x=0 或 x=2 或 x=4 B. x+y−1 x−y−1 D. x−y+1 x+y+1

10. 已知 a=2012x+2013，b=2014x+2015，c=2013x+2013，则 2c−a−b 2 等于 ( )

A. −4

B. 4

C. −8

D. 8

二、填空题（共6小题；共18分）

11. 当 x=−7 时，代数式 2x+5 ⋅ x+1 − x−3 x+1 的值是；

12. 6×106 ÷ −3×102 =．

13. 若 a− =1，则 a 的取值范围为 14. 若 a−a=3，则 a2+a2=．

15. 已知代数式 3x2−4x+6 的值为 9，则代数式 x2−3x+6 的值为

16. 7 张如图1的长为 a，宽为 b a>

本文来源：http://www.guakaob.com/chuzhong/525432.html