【www.guakaob.com--初三】
九年级(9th Grade)是初中的最后一年,在中国称做初三,在香港称做中三,在台湾曾经称做国三,欧美称做九年级。由于即将面临升读高中,因此九年级是仅次于十二年级(也称作高三)排名第二的重要年级。中国招生考试网www.chinazhaokao.com 小编为大家整理的相关的人教版九年级上册数学复习题21答案供大家参考选择。1.解:(1)196x²-1=0,移项,得196x²=1,直接开平方,得14x=±1,x=± 1/14,∴原方程的解为x_1=1/14,x_2=-1/14.
(2)4x²+12x+9=81,原方程化为x²+3x-18=0,∵a=1,b=3,c=-18,b²-4ac=3²-4×1×(-18)=81>0,∴x= (-3±√81)/(2×1)=(-3±9)/2,∴x_1=-6,x_2=3.
(3)x²-7x-1=0,∵a=1,b=-7,c=-1,b²-4ac=(-7)²-4×1×(-1)=53>0,∴x= (-(-7)±√53)/2=(7±√53)/2,∴x_1=(7+√53)/2,x_2=(7-√53)/2.
(4)2x²+3x=3,原方程化为2x²+3x-3=0,∵a=2,b=3,b=-3,b²-4ac=3²-4×2×(-3)=33>0,∴x= (-3±√33)/(2×2)=(-3±√33)/4,∴x_1=(-3+√33)/4,x_2=(-3-√33)/4.
(5)x²-2x+1=25,原方程化为x²-2x-24=0,因式分解,得(x-6)(x+4)=0,∴x-6=0或x+4=0,∴x_1=6,x_2=-4.
(6)x(2x-5)=4x-10,原方程化为(2x-5)(x-2)=0,,2x-5=0或x-2=0,∴x_1=5/2,x²=2.
(7)x²+5x+7=3x+11,原方程化为x²+2x-4=0,∵a=1,b=2,c=-4,b²-4ac=2²-4×1×(-4)=20>0,∴x= (-2±√20)/(2×1)=(-2±2√5)/2=-1±√5,∴x_1=-1+√5,x_2=-1-√5.
(8)1-8x+16x²=2-8x,原方程化为(1-4x)(-1-4x)=0,,1-4x=0或-1-4x=0,∴x_1=1/4,x_2=-1/4.
2.解:设其中一个数为(8-x),根据题意,得x(8-x)=9.75,整理,得x²-8x+9.75=0,解得x_1=6.5,x_2=1.5.当x=6.5时,8-x=1.5;当x=1.5时,8-x=6.5.答:这两个数是6.5和1.5.
3.解:设矩形的宽为x cm,则长为(x+3)cm.由矩形面积公式可得x(x+3)=4,整理,得x²+3x-4=0,解得x_1=-4,整理,得x²+3x-4=0,解得x_1=-4,x_2=1.因为矩形的边长是正数,所以x=-4不符合题意,舍去,所以x=1,所以x+3=1+3=4.答:矩形的长是4cm,宽是1cm.
4.解:设方程的两根分别为x_1,x_2.
(1)x_1+x_2=5,x_1∙x_2=-10.
(2) x_1+x_2=-7/2,x_1∙x_2=1/2.
(3)原方程化为3x²-2x-6=0,∴x_1+x_2=2/3,x_1∙x_2=-2.
(4)原方程化为x²-4x-7=0,∴x_1+x_2=4,x_1∙x_2=-7.
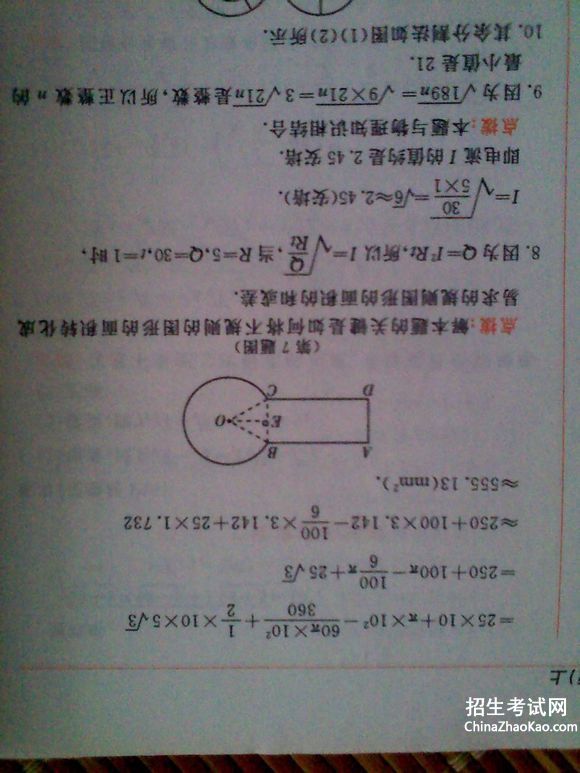
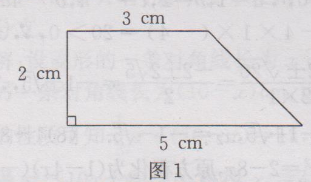
5.解:设梯形的伤低长为x cm ,则下底长为(x+2)cm,高为(x-1)cm,根据题意,得1/2 【x+(x+2)】∙(x-1)=8,整理,得x²=9,解得x_1=3,x_2=-3.因为梯形的低边长不能为负数,所以x=-3不符合题意,舍去,所以x=3,所以x+2=5,x-1=2.画出这个直角梯形如图1所示.
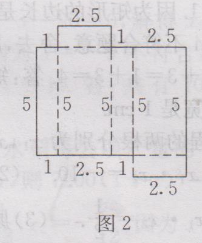
6.解:设这个长方体的长为5x cm,则宽为2 x cm,根据题意,得2x²+7-4=0,解得x_1=1/2,x_2=-4.因为长方体的棱长不能为负数,所以x=-4不合题意,舍去,所以x= 1/2.所以这个长方体的长为5x=1/2×5=2.5(cm),宽为2x=1(cm).画这个长方体的一个展开图如图2所示.(注意:长方体的展开图不唯一)
7.解:设应邀请x个球队参加比赛,由题意可知(x-1)+(x-2)+…+3+2+1=15,即1/2 x(x-1)=15,解得x_1=6,x_2=-5.因为球队的个数不能为负数,所以x=-5不符合题意,应舍去,所以x=6.答:应邀请6个球队参加比赛.
8.解:设与墙垂直的篱笆长为x m,则与墙平行的篱笆 为(20-2x)m.根据题意,得x(20-2x)=50,整理,得x²-10x+25=0,解得x_1=x_2=5,所以20-2x=10(m).答:用20m长的篱笆围城一个长为10m,宽为5m的矩形场地.(其中一边长为10m,另两边均为5m)
9.解:设平均每次降息的百分率变为x,根据题意,得2.25%(1-x)²=1.98%,整理,得(1-x)²=0.88,解得x_1=1-√0.88,x_2=1+√0.88.因为降息的百分率不能大于1,所以x=1+√0.88不合题意,舍去,所以x=1-√0.88≈0.0619=6.19%.答:平均每次降息的百分率约是6.19%.
10.解:设人均收入的年平均增长率为x,由题意可知12000(x+1)²=14520,解这个方程,得x+1=±√(1.21,)∴x=√1.21-1或x=-√1.21-1,又∵x=-√1.21-1不合题意,舍去,∴x=(√1.21-1)×100%=10%.答:人均收入的年平均增长率是10%.
11.解:设矩形的一边长为x cm,则与其相邻的一边长为(20-x)cm,由题意得x(20-x)=75,整理,得x²-20x+75=0,解得x_1=5,x_2=15,从而可知矩形的一边长15cm,与其相邻的一边长为5cm.当面积为101cm²时,可列方程x(20-x)=101,即x²-20x+101=0.∵△=-4<0,∴次方程无解,∴不能围成面积为101cm²的矩形.
12.解:设花坛中甬道的宽为x m.梯形的中位线长为1/2 (100+180)=140(m),根据题意,得1/2(100+180)×80×1/6=80∙x∙2+140x-2x²,整理,得3x²-450x+2800=0,解得x_1=(450+√168900)/6=75+5/3 √1689,x_2=(450-√168900)/6=75-5/3 √1689.因为x=75+5/3 √1689不符合题意,舍去,所以x=75-5/3 √1689≈6.50(m).故甬道的宽度约为6.50m.
13.解:(1)5/4=1.25(m/s),所以平均每秒小球的滚动速度减少1.25m/s.
(2)设小球滚动5m用了x s.(5+(5-1.25x))/2x=5,即x²-8x+8=0,解得x_1=4+2√2 (舍),x_2=4-2√2≈1.2.答:小球滚动5 m 约用了1.2s.
1、如图,火车匀速通过隧道(隧道长大于货车长)时,火车进入隧道的时间与火车在隧道内的长度之间的关系用图象描述大致是 ( )
2、 抛物线 的对称轴是 ( )
(A) 直线x=1 (B) 直线x=3
(C) 直线x=-1 (D) 直线x=-3
3、已知二次函数 ,当b从-1逐渐变化到1的过程中,它所对应的抛物线位置也随之变动.关于抛物线的移动方向的描述中,正确的是( )
A.先往左上方移动,再往左下方移动 B.先往左下方移动,再往左上方移动
C.先往右上方移动,再往右下方移动 D.先往右下方移动,再往右上方移动
4、已知函数 的图象与x轴有交点,则k的取值范围是( )
5、 若二次函数 (a,b为常数)的图象如图,则a的值为( )
A. 1 B. C. D. -2
6、二次函数 的图像可以由二次函数 的图像平移而得到,下列平移正确的是 ( )
A.先向左平移2个单位,再向上平移1个单位
B.先向左平移2个单位,再向下平移1个单位
C.先向右平移2个单位,再向上平移1个单位
D.先向右平移2个单位,再向下平移1个单位
7、已知:a>0,b<0,c<0,则二次函数 的图像可能是( )
A B C D
8、已知a=-1,点(a-1,y1),(a,y2),(a+5,y3)都在函数 的图象上,则 ( )
A.y1<y2<y3 B.y1<y3<y2 C.y3<y2<y1 D.y2<y1<y3
9、如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C-D-E上移动,若点C、D、E的坐标分别为(-1,4)、(3,4)、(3,1),点B的横坐标的最小值为1, 则点A的横坐标的最大值为( )
A、1 B、2 C、3 D、4
第9题 第10题
10、如图6,抛物线 与 交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B、C.则以下结论:
①无论取何值, 的值总是正数.
②.a=1
③当x=0时, .
④.2AB=3AC
其中正确结论是( )
A.①② B.②③ C.③④ D.①④
11、将抛物线 先向左平移2个单位,再向下平移3个单位,那么所得抛物线的函数关系式是( )
A. B. C. D.
二、解答题
12、直线 与坐标轴分别交于A、B两点,动点P、Q同时从点O出发,同时到达点A,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O→B→A运动.
(1)直接写出A、B两点的坐标;
(2)设点Q的运动时间为t秒, 的面积为s,求出s与t之间的函数关系式,并求出t的取值范围;
13、如图,抛物线 经过点A(1,0)和点P(3,4).
(1)求此抛物线的解析式,写出抛物线与x轴的交点坐标和顶点坐标.
(2)若抛物线与轴的另一个交点为B,现将抛物线向射线AP方向平移,使P点落在M点处,同时抛物线上的B点落在点D(BD∥PM)处.设抛物线平移前P、B之间的曲线部分与平移后M、D之间的曲线部分,与线段MP、BD所围成的面积为m, 线段 PM的长度为n,求m与n的函数关系式.
14、如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S .
(1)求S与x的函数关系式;
(2)如果要围成面积为45 的花圃,AB的长是多少米?
(3)能围成面积比45 更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.
15、如图,在平面直角坐标系中,直线y=-2x+42交x轴与点A,交直线y=x于点B,抛物线 分别交线段AB、OB于点C、D,点C和点D的横坐标分别为16和4,点P在这条抛物线上.
(1)求点C、D的纵坐标.
(2)求a、c的值.
(3)若Q为线段OB上一点,且P、Q两点的纵坐标都为5,求线段PQ的长.
(4)若Q为线段OB或线段AB上的一点,PQ⊥x轴,设P、Q两点之间的距离为d(d>0),点Q的横坐标为m,直接写出d随m的增大而减小时m的取值范围.
16、如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y( ).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
17、如图,在△AOB中, , ,矩形CDEF的顶点C、D、F分别在边AO、OB、AB上。
(1)若C、D恰好是边AO,OB的中点,求矩形CDEF的面积;
(2)若 ,求矩形CDEF面积的最大值。
18、对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如: ; ;
解决下列问题:
(1)填空: = ;如果 ,则x的取值范围为 .
(2)①如果 ,求x的值;
②根据①,你发现了结论“如果 ,那么 (填a,b,c的大小关系)”.证明你发现的结论;
③运用②的结论,填空:
,则x+y= .
(3)在同一直角坐标系中作出函数y=x+1, ,y=2-x的图象(不需列表描点).通过观察图象,填空: 的最大值为 .
19、如图,已知抛物线 的对称轴为直线x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
(1)求这条抛物线所对应的函数解析式;
(2)在抛物线的对称轴直线x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标;
(3)设点P为抛物线的对称轴直线x=1上的一动点,求使∠PCB=90°的点P的坐标.
20、改革开放以来,某镇通过多种途径发展地方经济,1995年该镇年国民生产总值为2亿元,根据测算,该镇国民生产总产值为5亿元时,可达到小康水平。(1)若从1996年开始,该镇国民生产总值每年比上一年增加0.6亿元,该镇通过几年可达到小康水平?
(2)设以2001年为第一年,该镇第x年的国民生产总值为y亿元,y与x之间的关系是 该镇那一年的国民生产总值可在1995年的基础上翻两番(即达到1995年的年国民生产总值的4倍)?
21、两个完全相同的矩形ABCD、AOEF按如图所示的方式摆放,使点A、D均在y轴的正半轴上,点B在第一象限,点E在x轴的正半轴上,点F在函数 的图象上,AB=1,AD=4.
(1)求k的值.
(2)将矩形ABCD绕点B顺时针旋转 得到矩形 ,边 交函数 的图象于点M,求 的长.
22、在梯形ABCD中,AB//CD,点E在线段DA上,直线CE与BA的延长线交于点G,
(1)求证:△CDE∽△GAE;
(2) 当DE:EA=1:2时,过点E作EF//CD交BC于点F且 CD=4,EF=6, 求AB的长
23、如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1) 求证:△ADF∽△DEC;
(2) 若AB=4,AD= ,AE=3,求ED,AF的长.
24、如图,一艘军舰从点A向位于正东方向的C岛航行,在点A处测得B岛在其北偏东 (即 ),航行75海里到达点D处,测得B岛在其北偏东 ,继续航行5海里到达C岛,此时接到通知,要求这艘军舰在半小时内赶到正北方向的B岛执行任务,则这艘军舰航行速度至少为多少时才能按时赶到B岛?
25、已知 ,延长BC到D,使CD=BC.取AB的中点F,连结FD交AC于点E.
(1)求 的值;
(2)若 ,求 的长.
26、有一河堤坝BCDF为梯形,斜坡BC坡度 ,坝高为5 m,坝顶CD = 6 m,现有一工程车需从距B点50 m的A处前方取土,然后经过B—C—D放土,为了安全起见,工程车轮只能停在离A、D处1 m的地方即M、N处工作,已知车轮半经为1 m,求车轮从取土处到放土处圆心从M到N所经过的路径长。( )
27、如图,某种新型导弹从地面发射点L处发射,在初始竖直加速飞行阶段,导弹上升的高度y(km)与飞行时间x(s)之间的关系式为 (0≤x≤10).发射3s后,导弹到达A点,此时位于与L同一水平面的R处雷达站测得AR的距离是2km,再过3s后,导弹到达B点.
(1)求发射点L与雷达站R之间的距离;
(2)当导弹到达B点时,求雷达站测得的仰角(即∠BRL)的正切值.
28、如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的俯角∠EAB为15°,码头D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数).
29、如图,A,B两座城市相距100千米,现计划要在两座城市之间修筑一条高等级公路(即线段AB)。经测量,森林保护区中心P点在A城市的北偏东30°方向,B城市的北偏西45°方向上。已知森林保护区的范围在以P为圆心,50千米为半径的圆形区域内,请问:计划修筑的这条高等级公路会不会穿越保护区?为什么?
30. 如图,在矩形 中, , .点 在 上, ,交 于 , ,交于 于 .点 从 点(不含 )沿 方向移动,直到使点 与点 重合为止.
(1)设 , 的面积为 .请写出 关于 的函数解析式.
(2)点 在运动过程中, 的面积是否有最大值,若有,请求出最大值及此时 的取值;若无,请说明理由.
上一篇:初三自我介绍范文600字
下一篇:虹口化学三模2016