【www.guakaob.com--初三】
2016级德州市初三期末考试成绩大排名的相关资料信息整理以供大家参考!以下是中国招生考试网www.chinazhaokao.com 分享的2016级德州市初三期末考试成绩大排名,希望能帮助到大家!
2016级德州市初三期末考试成绩大排名
查询方法:直截输入地名和
教育,就会出现当地的各种
教育网,进入后,根据你所查考试的类型,一步步进入即可。一般省通考的,在省级以下网上查,市通考的,在市级以下网上查,以次类推。或者输入学校官网搜索教务系统就可以找到成绩排名。
相关阅读:
初三数学期末试题
(答题时间:60分钟)
一. 选择题:(每题3分,共30分)
1. 函数

中自变量的取值范围是( )
A.
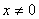
B.
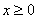
C.
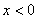
D.
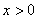
2. 如果一次函数
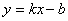
的图象经过第一、三、四象限,那么( )
A.
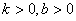
B.
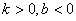
C.
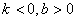
D.
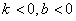
3. 一次函数

中,函数图象

随

的增大而减小,且其图象不经过第一象限,则
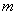
的取值范围是( )
A.
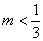
B.
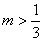
C.
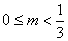
D.
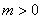
4. 两直线
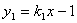
,
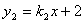
的交点在

轴上,则
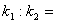
( )
A.
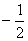
B.

C.

D. 2
5. 若⊙A的半径是5,圆心A的坐标为(3,4),点P的坐标为(5,8),则点P的位置在( )
A. ⊙A内 B. ⊙A上 C. ⊙A外 D. 不能确定
6. 在⊙O中,
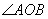
=
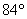
,则弦AB所对的圆周角是( )
A.
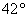
B.

C.
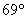
D.
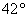
或

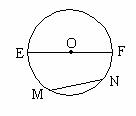
7. 如图:EF是⊙O的直径,OE=5cm,弦MN=8cm,则E、F两点到直线MN的距离之和为( )
A. 12cm B. 6cm C. 8cm D. 3cm
8. 下列判断正确的是( )
A.

的圆周角所对的弦是直径,所对的弧是半圆
B. 圆周角的度数等于圆心角的一半
C. 平分一条弧的直线必垂直平分弧所对的弦
D. 同圆或等圆中,弦相等则它们所对的弧相等
9. 在四边形ABCD中,若
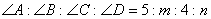
,则( )
A.
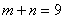
B.

C.
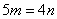
D. 以上都不对
10. 在平面直角坐标系中,有四个点A(
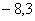
),B(
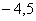
),C(
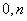
),D(
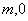
),若使四边形ABCD的周长最短,则
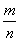
值( )
A.
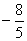
B.

C.
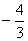
D.
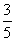
二. 填空题:(每题3分,共24分)
11. 一个点到圆的最小距离是
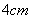
,最大距离是
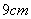
,则该圆的直径为 。
12. ⊙O直径为10,弦AB为8,P是AB上的一个动点,则OP的取值范围为 。
13.
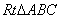
中,
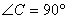
,

,以点C为圆心,CA为半径的圆交BA于D,交BC于E,则
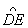
的度数为 。
14. 设AB是⊙O的一条弦,AB=1,C是圆周上一点,
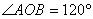
,则圆的半径是
。
15. 如图:一束光线从

轴上的点A(0,1)出发,经

轴上的点 C反射后经过B(3,3),则光线从A到B所经过的路程是 。

16. 一次函数的图象经过点M(3,4)且于

轴的负半轴、

轴的正半轴分别交于A、B两点,当|OA|+|OB|=5时,此函数的解析式为 。
17. 函数
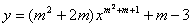
是一次函数,此函数图象与两个坐标轴围成的三角形的面积为 。
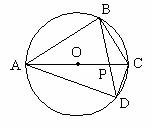
18. 如图,已知:四边形ABCD内接于直径为3的圆O,对角线AC是直径,对角线AC和BD的交点是P,AB=BD,且PC=0.6,则四边形ABCD的周长是 。
三. 解答题:(19至25题每题8分,26题10分)
19. 已知:
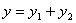
,其中
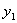
与

成正比例,
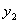
与
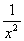
成正比例,且
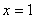
时,
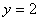
;当
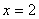
时,

,求:

与

的函数关系式。
20. 已知:一次函数
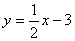
的图象与

轴、

轴分别交于A、B两点,过C(4,0)作AB的垂线交AB于E,交

轴于D,求点D、E的坐标。
21. 直线
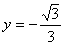
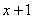
与

轴、

轴分别交于A、B,以线段AB为直角边在第一象限作等腰直角三角形
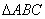
,使

,如果第二象限内有一点P(

),使
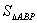
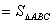
,求
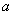
的值。
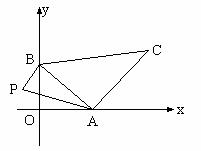
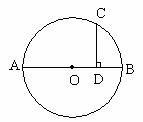
22. 如图,已知:AB是圆O的直径,CD⊥AB于点D,AB=

,CD=1(
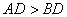
)。求BD的长。
23. 设一圆的圆心为O,AB、CD是两条在点O两侧的平行弦,已知AB=40,CD=48,⊙O的半径为25,求AC的长。
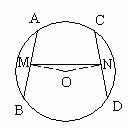
24. 如图,已知:⊙O中,M、N分别是两条不平行的弦AB、CD的中点,且AB=CD,求证:
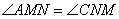
。

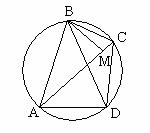
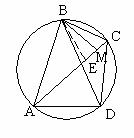
25. 如图,已知:点A、B、C、D顺次在⊙O上,
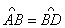
,BM⊥AC于点M,求证:AM=DC+CM。
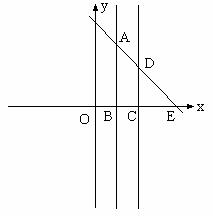
26. 已知:一次函数

具有性质:

随

的增大而减小,又直线

分别与直线
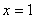
,
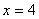
相交于A、D,且点A在第一象限内,直线
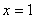
,
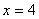
分别与

轴相交于B、C。
(1)要使四边形ABCD为凸四边形,试求
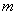
的取值范围。
(2)已知四边形ABCD为凸四边形,直线

与

轴交于E,当
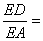
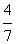
时,求这个一次函数的解析式。
(3)在(2)的条件下,设直线

与

轴相交于点F,求证:D是
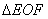
的外心。
【试题答案】
一.
1. D 2. A 3. C 4. A 5. A 6. D 7. B 8. A 9. D 10. B
二.
11. 5或13cm 12.
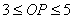
13.

14.
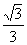
15. 5
16.
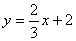
17. 8 18.
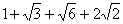
三.
19.
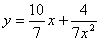
20. 解:易知A(6,0),B(0,
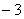
),C(4,0)
∴ OA=6,OB=3,OC=4 由
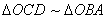
得
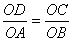
∴ OD=8 ∴ D(0,8) ∴ 直线CD:
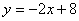
由

得
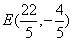
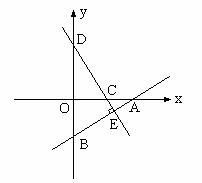
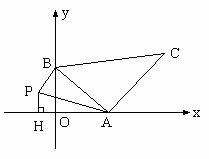
21. 解:A(
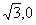
),B(0,1) ∴ OA=
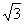
,OB=1
∴

∴
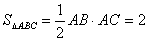
作PH⊥OA于H,则

∴
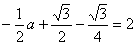
∴
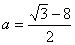
22.
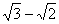 提示:
提示:连AC、BC,用射影定理
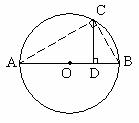
23.

或
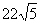 提示:
提示:用垂径定理,作弦心距
24.
提示:连OM、ON,则OM⊥AB,ON⊥CD,又由于AB=CD,故OM=ON,所以
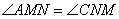
25.
提示:在AM上截取AE=CD,连BE,则有
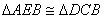
(SAS),故BE=BC,EM=MC。
26. 解:
(1)直线

应与

轴相交,交点E(
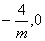
)
在点C(4,0)的右侧,故
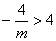
,
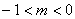
(2)∵ DC∥AB ∴
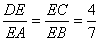
∵
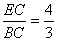
∵
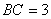
∴
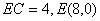
∴
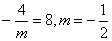
∴
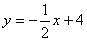
(3)易知OC=EC=4 ∵ DC∥OF ∴ DF=DE
又 ∵
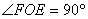
∴ OD=DF=DE
∴ D是
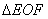
的外心
本文来源:http://www.guakaob.com/chuzhong/807540.html








 得
得




