高二数学必修2第一章测试

【www.guakaob.com--高一】

高二数学必修2第一章测试(一)
高二数学必修2第一章测试题

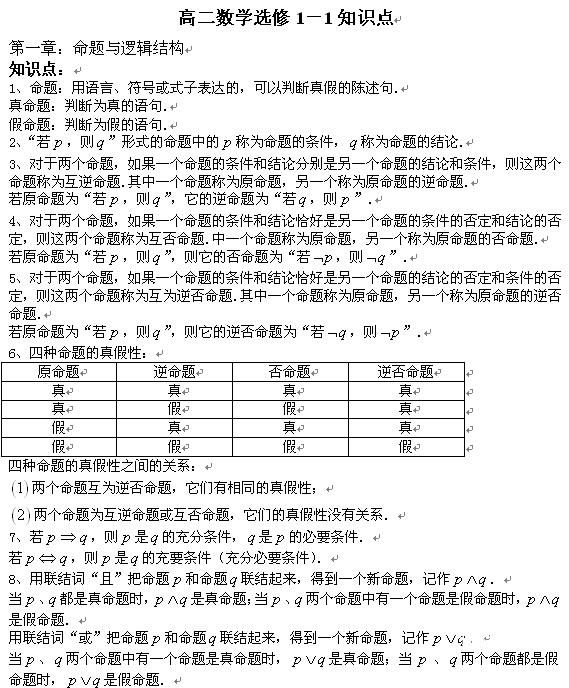
高一数学必修2第一章测试题

一、选择题：

1．若一个几何体的三视图都是等腰三角形，则这个几何体可能是（ ） A．圆锥 B．正四棱锥 C．正三棱锥 D．正三棱台

2.已知圆柱与圆锥的底面积相等，高也相等，它们的体积分别为V1和V2，则V1：V2=（ ）

A. 1：3 B. 1：1 C. 2：1 D. 3：1

3.过圆锥的高的三等分点作平行于底面的截面，它们把圆锥侧面分成的三部分的面积之比为（ ）

A.1：2：3 B.1：3：5 C.1：2：4 D.1：3：9 4.棱长都是1的三棱锥的表面积为（ ） A.

B. 23 C. 3 D. 4

5.如果两个球的体积之比为8:27,那么两个球的表面积之比为（ ） A.8:27 B. 2:3 C.4:9 D. 2:9

6.有一个几何体的三视图及其尺寸如下（单位cm），则该几何体的表面积及体积为：

（ ）

主视图 侧视图 俯视图 A.24πcm2

，12πcm3

B.15πcm2

，12πcm

3

C.24πcm2，36πcm3

D.以上都不正确 7．下列几种说法正确的个数是（ ）

①相等的角在直观图中对应的角仍然相等

②相等的线段在直观图中对应的线段仍然相等 ③平行的线段在直观图中对应的线段仍然平行

④线段的中点在直观图中仍然是线段的中点 A．1 B．2 C．3 D．4 8．正方体的内切球和外接球的半径之比为（ ）

A

B

2 C

． D

9．将一圆形纸片沿半径剪开为两个扇形，其圆心角之比为3∶4. 再将它们卷成两个圆锥侧面，则两圆锥的高之比为（ ） A．3∶4 B．9∶16 C．27∶64 D．都不对

10．一个棱柱至少有点最少的一个棱台有 ___条侧棱。 11．图（1）为长方体积木块堆成的几何体的三视图，此几何体共由________块木块堆成;

图（2）中的三视图表示的实物为_____________。 图（1）

图（2）

12．已知一个长方体共一顶点的三个面的面积分别是2、3、6，这个长方体的对角线长是________；若长方体的共顶点的三个面的面积分别为3,5,15，则它的体积为________.

13．圆台的较小底面半径为1，母线长为2，一条母线和底面的一条半径有交点且

成60角,则圆台的侧面积为____________。 14．(1)等体积的球和正方体,它们的表面积的大小关系是S球___S正方体；

(2)一个直径为32厘米的圆柱形水桶中放入一个铁球，球全部没入水中后，水面升高9厘米则此球的半径为______厘米. 15．画出下列空间几何体的三视图（图②中棱锥的各个侧面都是等腰三角形）．

16．已知圆台的上下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长

17. （如图）在底半径为2，母线长为4

的圆锥中内接一个高为的表面积.

18．养路处建造圆锥形仓库用于贮藏食盐（供融化高速公路上的积雪之用），已建

的仓库的底面直径为12M，高4M，养路处拟建一个更大的圆锥形仓库，以存放更多食盐，现有两种方案：一是新建的仓库的底面直径比原来大4M（高不变）；二是高度增加4M (底面直径不变)。

（1） 分别计算按这两种方案所建的仓库的体积； （2） 分别计算按这两种方案所建的仓库的表面积； （3） 哪个方案更经济些？

一、选择题：

1.C 2.D 3.B 4.A 5.C 6.A 7.B 8.D 9.D

10. 5,4,3. 符合条件的几何体分别是：三棱柱，三棱锥，三棱台 11. （1）4 （2）圆锥 12.

15

13. 6 画出圆台，则r1

1,r22,l

2圆台侧面S,

1

r(

2

r)l

6

V4R3a3,a14. （1）

设

3RVShr2h4

R3,R（2）12

312

17. （12分）解：

(25)l(2252),l

297

18. （14分）

解：圆锥的高

hr1， S表面2S底面S侧面2(2

　　

MV1Sh116

2

25619. 如果按方案一，仓库的底面直径变成16,133243(M3)

2

V1112

288如果按方案二，仓库的高变成8M，23Sh3283(M3)

（2）如果按方案一，仓库的底面直径变成16M,半径为8M.

棱锥的母线长为

l

则仓库的表面积S2

18(M)

如果按方案二，仓库的高变成8M.

棱锥的母线长为

l10 则仓库的表面积S261060(M2) （3）V2V1 ，S2S1 方案2经济

高二数学必修2第一章测试(二)
高二数学必修二第一章检测题

高二数学必修二第一章检测题

宋秀芝

组长检查前置作业完成情况（请在相应空格内画√）

※优秀 全部完成且卷面整洁 ※良好 完成80℅以上且卷面整洁 ※一般 完成80℅-50℅左右，卷面一般 ※较差 完成50℅以下，卷面较差

一 选择题

1．下面描述中，不是棱锥的几何结构特征的为( )

A．三棱锥有四个面是三角形

B．棱锥都是有两个面是互相平行的多边形 C．棱锥的侧面都是三角形 D．棱锥的侧棱交于一点

2．给出下列几种说法：①经过圆柱任意两条母线的截面是一个矩形；②连接圆柱上、下底面圆周上两点的线段是圆柱的母线；③圆柱的任意两条母线互相平行．其中正确的个数为( )

A．0 B．1 C．2 D．

3

3．用一个平面去截一个几何体，得到的截面是圆面，这个几何体不可能是( )

A．圆锥 B．圆柱 C．球 D．棱柱

4．一个空间几何体的正视图与侧视图均为全等的等腰三角形，俯视图为一个圆及其圆心，那么这个几何体为( )

A．棱锥 B．棱柱 C．圆锥 D．圆柱

5．一个几何体的三视图如图，则组成该组合体的简单几何体为( )

A．圆柱与圆台

B．四棱柱与四棱台

C．圆柱与四棱台

D．四棱柱与圆台

6．某几何体的三视图如下图所示，则该几何体为（ ）

A．三棱柱 B．三棱锥 C．圆锥 D．四棱锥

7．给出以下关于斜二测直观图的结论，其中正确的个数是( )

①角的水平放置的直观图一定是角． ②相等的角在直观图中仍相等． ③相等的线段在直观图中仍然相等．

④若两条线段平行，则在直观图中对应的两条线段仍然平行． A．0 B．1 C．2 D．3

8. 已知一个正方形的直观图是一个平行四边形，其中有一边长为4，则此正方形的面积是( )

A．16 B．64 C．16或64 D．无法确定 9．已知一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是( )

A.1＋2π1＋4π2π B.4π C.1

＋2π1＋4

π

D.2π

10．轴截面是正三角形的圆锥称作等边圆锥，则等边圆锥的侧面积是底面积的( )

A．4倍 B．3倍 C.2倍 D．2倍

11．已知正六棱台的上、下底面边长分别为2和4，高为2，则体积为( )

A．323 B．283 C．3 D．203

12．长方体三个面的面积分别为2、6和9，则长方体的体积是( )

A．63 B．36 C．11 D．12

二填空题

13．一个圆锥的母线长是20cm，母线与轴的夹角为300

，则圆锥的底面半径是

14．如图是一个几何体的三视图，该几何体的体积为.

（第14题图）

15．一个正方体的顶点都在球面上，它的棱长是acm,球的体积是

16．一个球的体积是100cm3，它的表面积是

17．一个圆台的上、下底面面积分别是πcm2和49πcm2，一个平行于底面的截面面积为25πcm2，则这个截面与上、下底面的距离之比是 ．

学生自评前置作业修改情况（请在相应空格内画√）

※优秀 全部完成且记录完整 ※良好 完成80℅以上，记录较完整。※一般 完成80℅-50℅左右，记录较完整。 ※较差 完成50℅以下，有记录不完整。

高二数学必修2第一章测试(三)
高二数学必修2第一章复习题(教师版)

高二数学必修2第一章复习题

一、选择题

1．(2011·全国高考)在一个几何体的三视图中，正视图和俯视图如图所示，则相应的侧视图可以为( )

2、（2013届北京西城区一模理科）某正三棱柱的三视图如图所示，其中

正（主）视图是边长为2的正方形，该正三棱柱的表面积是C A

．6 B

．12C

．12

D．24

（ ）

3 ．（北京市东城区普通高中示范校

3月联考综合练习（二）数学（理）试题 ）已知底面为正方

形的四棱锥，其一条侧棱垂直于底面，那么该四棱锥的三视图可能是下列各图中的 C

正视图 侧视图 正视图 侧视图

正视图 侧视图

正视图 侧视图

俯视图 俯视图

俯视图

俯视图

A．

（ ）

B． C． D．

4．（北京市海淀区北师特学校2013届高三第四次月考理科数学）已知一个几何体是由上下两部分构成的组合

体，其三视图如下，若图中圆的半径为1，等腰三角形的腰长为 A．

，则该几何体的体积是

（A ）

4

3

B．2

C．

8 3

D．

10

3

5．（北京市西城区2013届高三上学期期末考试数学理科试题）某四面体的三视图如图所示．该四面体的六条【高二数学必修2第一章测试】

棱的长度中，最大的是 C A

．

6.一个几何体的三视图如图所示，该几何 体的表面积是B

（ ）

C

．D

．B

．正（主）视图 侧（左）视图

俯视图

A

．16B

．12

C

．8D

．4（ ）

7．（北京市丰台区2013届高三上学期期末考试 数学理试题 ）如图，

的

等腰直角三角形，则该三棱锥的四个面的面积中最大的是 A

8．已知一个空间几何体的三视图如图所示，根据图中标出的尺寸，

（ ）

D．2

B

．C．1

可得这个几何体的全面积为（ B ）

A

．10 C

．14

9．（北京市房山区2013届高三上学期期末考试数学理试题 ）【高二数学必修2第一章测试】

若正三

B

．10 D

．14

棱柱的三视图如图所示，该三棱柱的D 表面积是

（ ）

A

C

．6

B

D

．6

10．(2012·台州模拟)用单位正方体搭一个几何体，使它的主视图和俯视图如图所示，则它的体积的最小值与最大值分别为(

)

A．9与13 B．7和10 C．10与16 D．10与15

【解析】 体积最小时如图(1)搭建，体积最大时如图(2)搭建．(图中方框内的数字代表搭起的小正方体的个数

)

故最小体积为10，最大体积为16. 【答案】 C 二、填空题

11．如图是利用斜二测画法画出的△ABO的直观图，已知O′B′＝4，且△ABO的面积为16，过A′作

A′C′⊥x′轴，则A′C′的长为___

2_____．

12．有一块多边形的菜地，它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示)，∠ABC＝45°，AB＝AD＝1，DC⊥BC，则这块菜地的面积为________．【高二数学必修2第一章测试】

【解析】 在直观图中，过点A作AE⊥BC，垂足为E， 则在Rt△ABE中，AB＝1，∠ABE＝45°，∴BE＝

2

2

而四边形AECD为矩形，AD＝1， ∴EC＝AD＝1，∴BC＝BE＋EC＝由此可还原原图形如图．

2

1. 2

在原图形中，A′D′＝1，A′B′＝2， B′C′＝

2

＋1， 2

且A′D′∥B′C′，A′B′⊥B′C′， ∴这块菜地的面积为

1

SA′D′＋B′C′)·A′B′ 2122

＝×1＋1×2＝2＋. 222【答案】 22

2

13．（2013届北京丰台区一模理科）某四面体的三视图如图所示，则该四面体的四个面中，直角三角形的面

积和是__2+5_____.

14.(2012·皖南八校模拟)已知三棱锥的直观图及

其俯视图与侧

(左)视图如下，俯视图是边长为2的正三角形，侧(左)视图是有一直角边为2的直角三角形，则该三棱锥的正(主)视图面积为________．

【解析】 由直观图、俯视图和侧视图可知，

该几何体为一个三棱锥，底面边长为2的正三角形，三棱锥的一条侧棱垂直底面，其高为2.故正视图为一个直角三角形，两直角边长均为2.

1

∴S2×2＝2.

2

【答案】 2

三、解答题

15．已知△ABC的直观图A′B′C′是边长为a的正三角形，求原△ABC的面积．

【解析】 建立如图所示的坐标系xOy′，△A′B′C′的顶点C′在y′轴上，A′B′边在x轴上， 把y′轴绕原点逆时针旋转45°得y轴，在y轴上取点C使OC＝2OC′，A、B点即为A′、B′点，长度不变．

已知A′B′＝A′C＝a，在△OA′C′中， OC′

sin∠OA′C′＝

A′C′

sin 45°

sin 120°6

所以OC′＝a＝a，

sin 45°2所以原三角形ABC的高OC＝6a， 16

所以S△ABC＝×a6aa2.

22

16．(2012·四平模拟)已知正三棱锥V—

ABC的正视图、侧视图和俯视图如图所示．

(1)画出该三棱锥的直观图； (2)求出侧视图的面积． 【解析】

(1)如图所示．

(2)根据三视图间的关系可得BC＝23， ∴侧视图中VA＝

高二数学必修2第一章测试(四)
高中数学必修二第一章测试题及答案(人教版)

第一章 空间几何体

一、选择题

1

)． 俯视图 (第1题) A．棱台 B．棱锥 C．棱柱 D．正八面体

2．如果一个水平放置的平面图形的斜二测直观图是一个底角为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积是( )．

1＋22＋2

C． 22

3．棱长都是1的三棱锥的表面积为( )．

A．

D．

9 B．5 ( 第 8 题 ) C．6 2

9．下列关于用斜二测画法画直观图的说法中，错误的是( )． ．．

15

2

A．2＋2 B． 12 D．

A．用斜二测画法画出的直观图是在平行投影下画出的空间图形

B．几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同 C．水平放置的矩形的直观图是平行四边形 D．水平放置的圆的直观图是椭圆

10．如图是一个物体的三视图，则此物体的直观图是( )．

A． B．23 C．3 D．4 4．长方体的一个顶点上三条棱长分别是3，4，5，且它的8个顶点都在同一球面上，则这个球的表面积是( )．

A．25π B．50π C．125π D．都不对 5．正方体的棱长和外接球的半径之比为( )． A．3∶1 B．∶2 C．2∶3 D．3∶3

6．在△ABC中，AB＝2，BC＝1.5，∠ABC＝120°，若使△ABC绕直线BC旋转一周，则所形成的几何体的体积是( )．

9753A．π B．π C．π D．π

22227．若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是( )．

A．130 B．140 C．150 D．160 8．如图，在多面体ABCDEF中，已知平面ABCD是边长为3的正方形，EF∥

3

AB，EF＝，且EF与平面ABCD的距离为2，则该多面体的体积为( )．

2

(第10题)

二、填空题

11．一个棱柱至少有______个面，面数最少的一个棱锥有________个顶点，顶点最少的一个棱台有________条侧棱．

12．若三个球的表面积之比是1∶2∶3，则它们的体积之比是_____________． 13．正方体ABCD－A1B1C1D1 中，O是上底面ABCD的中心，若正方体的棱长为a，则三棱锥O－AB1D1的体积为_____________．

14．如图，E，F分别为正方体的面ADD1A1、面BCC1B1的中心，则四边形BFD1E在该正方体的面上的射影可能是___________．

第 1 页 共 2 页

(第14题)

(第19题)

15．已知一个长方体共一顶点的三个面的面积分别是2、、，则这个长方体的对角线长是___________，它的体积为___________．

16．一个直径为32厘米的圆柱形水桶中放入一个铁球，球全部没入水中后，水面升高9厘米则此球的半径为_________厘米．

三、解答题

17．有一个正四棱台形状的油槽，可以装油190 L，假如它的两底面边长分别等于60 cm和40 cm，求它的深度．

18 *．已知半球内有一个内接正方体，求这个半球的体积与正方体的体积之比．[提示：过正方体的对角面作截面]

19．如图，在四边形ABCD中，∠DAB＝90°，∠ADC＝135°，AB＝5，CD＝22，AD＝2，求四边形ABCD绕AD旋转一周所成几何体的表面积及体积．

20．养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用)，已建的仓库的底面直径为12 m，高4 m，养路处拟建一个更大的圆锥形仓库，以存放更多食盐，现有两种方案：一是新建的仓库的底面直径比原来大4 m(高不变)；二是高度增加4 m(底面直径不变)．

(1)分别计算按这两种方案所建的仓库的体积； (2)分别计算按这两种方案所建的仓库的表面积； (3)哪个方案更经济些？

第 2 页 共 2 页

高二数学必修2第一章测试(五)
万全高中高二数学必修2第一章测试卷

万全高中高二数学必修2第一章练习卷

1、右图所示的直观图，其原来平面图形的面积是

A 4 B 4

2 C 22 D 1

2.下面的图形可以构成正方体的是（

）

3、若一个几何体的正视图、侧视图、俯视图均为圆，则这个几何体可能是（

） Ａ． 圆柱 Ｂ． 圆台 Ｃ． 圆锥 Ｄ．球体

4.如果轴截面为正方形的圆柱的侧面积是4，那么圆柱的体积等于（ ） A  B 2 C 4 D 8 5、一个圆锥的俯视图和正视图及其尺寸如下（单位cm），则该几何体的表面积及体为( )

2323

A.24πcm，12πcm B.15πcm，12πcm

23

C.24πcm，36πcmD.以上都不正确

6．已知一个几何体的三视图如下图所示，则此几何体的表面积为（ ）

2

A.4a5a俯视图 正视图 侧视图 7. 如图，一个简单空间几何体的三视图其正视图与侧视图都是边长为2 的正三角形, 其俯视图轮廓为正方形，则其体积是（ ） A B． C D．

8．面积为Q的正方形，绕其一边旋转一周，则所得几何体的侧面积为 （ ）

(A)Q (B)2Q (C)3Q (D)4Q

9.若一个三角形采用斜二测画法作出其直观图，则其直观图的面积是原来三角形面积的

（ ） A．

22倍 B．2倍 C． 倍 D．2倍 42

11.一个三棱锥，如果它的底面是直角三角形，那么它的三个侧面（ ） A．必定都不是直角三角形 B．至多有一个直角三角形 C．至多有两个直角三角形

D．可能都是直角三角形

12.如果轴截面为正方形的圆柱的侧面积是4，那么圆柱的体积等于（ ） A. B.2 C.4 D.8

13．将棱长为1的正方体木块切削成一个体积最大的球，则该球的体积为 （ ）

3

(A)2 42



(B)3 (C)6 (D)3

14．已知一个铜质的五棱柱的底面积为24cm2,高为9cm，现将它熔化后铸成一个正方体的铜块（不计损耗），那么铸成的铜块的棱长是（ ）

(A) 8cm (B) 6cm (C) 4cm (D) 2cm 二、填空题

15．球的表面积扩大为原来的4倍,它的体积扩大为原来的 _________ 倍

16.一个正四棱柱（底面为正方形的直棱柱）的侧面展开图是一个边长为4的正方形，则它的体积为___________.

15、如右图是一个底面直径和高都是4的圆柱的侧面积为 ___ ．．．

（最后的结果保留π） 16．若正方体外接球的体积是

32

，则正方体的棱长等于 3

17

则这个平面图形的面积是 ．

x

′

18

19．长方体ABCDA中，已知，BCDAB4AD1111113，则此长方体外接球表面积的取值范围是 ．

本文来源：http://www.guakaob.com/gaozhong/504025.html