2015石景山一模文科数学

【www.guakaob.com--高三】

2015石景山一模文科数学(一)
北京市2015年石景山区高三一模数学试题(文科)

2015石景山一模文科数学(二)
2015石景山一模文科数学带答案

2015年石景山区高三统一测试

数学（文）

一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．已知集合A{1,2}，BxZ0x2，则AA．{0} B．{2} C．{0,1,2} D． 2．函数ysin(x)1的图象（ ） A．关于x



B=（ ）



2

对称 B．关于y轴对称 C．关于原点对称 D．关于x对称

3．两旅客坐火车外出旅游，希望座位连在一起，且有一个 靠窗，已知火车上的座位的排法如图所示，则下列座位号码 符合要求的是（ ） A．48，49 B．62，63 C．75，76 D．84，85

4．如图，在66的方格纸中，若起点和终点均在格点的向量a,b,c满足

cxayb,(x,yR)，则xy（ ）

A．0 B． 1 C

． D．

135

1

5．阅读右面的程序框图，若输出的y，则输入

2

的x的值可能为（ ）

A．1 B．0 C． 1 D．5 6．函数 f(x)(xa)(xb)（其中ab）的图象 如右图所示，则函数g(x)ab的大致图象是（

x

A B C

高三数学（文科）答案 第1页（共8页）

2015石景山一模文科数学(三)
2015年北京市石景山区高三一模数学(文)试题及答案

2015年石景山区高三一模

数 学（文）

本试卷共6页，150分.考试时长120分钟.请务必将答案答在答题卡上，在试卷上作答无效.考试结束后上交答题卡.

第一部分（选择题 共40分）

一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．已知集合A{1,2}，BxZ0x2，则A2．函数ysin(x)1的图象（ ）A．关于x



B=（ ） A．{0} B．{2} C．{0,1,2} D．



2

对称 B．关于y轴对称 C．关于原点对称 D．关于x对称

3

A．48，49 B．62，63 C．75，76 4．如图，在66则xy（ ）A．0 cxayb,(x,yR)，

1

5．阅读右面的程序框图，若输出的y2

A．1 B．0 C． 1 D．6．函数 f(x)(xa)(xb)（其中abg(x)axb的大致图象是（ ）

A B C 7．如图，网格纸上小正方形的边长为1各条棱中，最长的棱的长度为（ ）A．8．如图，正方体ABCD-A1B1C1D1的棱长为1，点上的动点，且动点P到直线A1D1的距离与点P A．圆 B．抛物线 C．双曲线 D二、填空题共6小题，每小题5分，共30分． 9．已知角的终边经过点P(x,6)，且tanxy20



10．设变量x,y满足约束条件xy70，x1



11．有甲、乙、丙、丁四位歌手参加比赛，其中只有一位获奖．有人走访了四位歌手，甲说：“是乙或丙获奖”，乙说：“甲、

丙都未获奖”，丙说：“我获奖了”，丁说：“是乙获奖了”.四位歌手的话只有两句是对的，则获奖的歌手是 12．在平面直角坐标系xOy中，已知点A(0,2)，B(2,0)，C(1,0)，分别以△ABC的 边AB、AC向外作正方形ABEF与ACGH，则直线FH的一般式方程为 ． 13．某学校拟建一块周长为400米的操场，如图所示，操场的两头是半圆形，中间区域是矩形，学生做操一般安排在矩形区域，为了能让学生的做操区域尽可能大，矩形的长应该设计成 米． 14．已知集合M{(x,y)|yf(x)}，若对于任意(x1,y1)M，存在(x2,y2)M，使得xxyy0成立，则称集合M是“垂直对点集”．给出下列四个集合：

12

12

2x

①M{(x,y)|yx+1}；②M{(x,y)|ylog2x}； ③M{(x,y)|y22}；④M{(x,y)|ysinx1}．

其中是“垂直对点集”的序号是 ．

三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．

Sn

),nN*均在函数yx的图象上． n

（Ⅰ）求数列an的通项公式；（Ⅱ）若bn为等比数列，且b11,bb12b38，求数列an+bn的前n项和Tn．

15．（本小题满分13分）设数列an的前n项和为Sn，点(n,

16．（本小题满分13分）在△ABC中，角A，B，C的对边分别为a，b，c

．已知

b，A3C． c（Ⅰ）求cosC的值；（Ⅱ）求sinB的值；

（Ⅲ）若bABC的面积．

17．（本小题满分13分） 已知高二某班学生语文与数学的学业水平测试成绩抽样统计如下表，若抽取学生n人，成绩分为

A（优秀）、B（良好）、C（及格）三个等级，设x，y分别表示语文成绩与数学成绩．例如：

表中语文成绩为B

x与y均为B等级的概率是0.18．

30%，求a，b值； （Ⅲ）已知a10,b8，求语文成绩为A等级的总人数比语文成绩为C等级的总人数少的概率.

C 18．（本小题满分14分）如图，已知AF平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，DAB90，AB//CD，AD=AF=CD=2，AB=4． （Ⅰ）求证：AC平面BCE；（Ⅱ）求三棱锥ACDE否存在一点M，使得BMCE ?若存在，确定M点的位置；若不存在，请说明理由．

x2y2

19．（本小题满分14分）如图，已知椭圆C：221(ab0)的离心率e，短轴的

2ba

右端点为B， M（1，0）为线段OB的中点．（Ⅰ）求椭圆C的方程；（Ⅱ）过点M任意作一条

直线与椭圆C相交于两点P，Q。试问在x轴上是否存在定点N，使得∠PNM =∠QNM 求出点N的坐标；若不存在，说明理由．

12

ax2x.（Ⅰ）若函数f(x)在定义域内单调递增，求实数a的取值范围； 2

11

（Ⅱ）若a，且关于x的方程f(x)xb在[1,4]上恰有两个不等的实根，求实数b的取值范围；

22

n

（Ⅲ）设各项为正数的数列an满足a11,an1lnanan2(nN*)，求证：an21.

20．(本小题满分13 分)已知函数f(x)lnx

2015年石景山区高三统一测试【2015石景山一模文科数学】

数 学（文）参考答案

三、解答题共6小题，共80分．

Sn

n，即Sn=n2．当n=1时，a1=S1=1……………1分 n

当n≥2时，anSnSn12n1；…………3分 当n=1时，a1=211=1 所以an2n1……………4分

15．（本小题共13分） （Ⅰ）依题意得

3(Ⅱ) bb得到b22，又b11，q2，bnb1qbb12328

n1

n1

， 2n1，…………8分 anbn2n12【2015石景山一模文科数学】

Tn(2120)(4121)(2n12n1)(21412n1)(20212n1)n22n1……………13分

16．（本小题共13分）(Ⅰ)因为ABCp，A3Cp，所以B2C． ……………………1分

2sinCcosCbcbsinB

又由正弦定理，得，， ，化简得，cosC．……………………4分 

sinCsinBsinCcsinC

(Ⅱ)因为C0,p，所以sinC．所以sinBsin2C2sinCcosC2．……7分

11

（Ⅲ）因为B2C，所以cosBcos2C2cos2C121．………………9分【2015石景山一模文科数学】

33

9b1()所以sinAsin(BC)……………11

分因为，

bc．…………12分 3c2119所以△ABC

的面积SbcsinA． ………………………13分

22218

17．（本小题共13分）(Ⅰ)由题意可知＝0.18，得n＝100.故抽取的学生人数是100. ………………2分

n

(Ⅱ) 由（Ⅰ）知n＝100，所以(79a)/100=0.3，故a＝14， ………………4分 而7＋9＋a＋20＋18＋4＋5＋6＋b＝100，故b＝17.……………6分

（Ⅲ）设“语文成绩为A等级的总人数比语文成绩为C等级的总人数少”为事件A,由(Ⅱ)易知a＋b＝31,且a≥10,b≥8,…7分 满足条件的（a，b）有（10,21），（11,20），（12,19），（13,18）, （14,17）,（15,16）,（16,15）,（17,14）,（18,13）,（19,12），（20,11）,（21,10）,（22,9）,（23,8），共有14组，……10分 其中b+11a+16的有3组，

………12分 3.………………13分

14

18．（本小题共14分）（Ⅰ）过C作CNAB，垂足为N，因为ADDC，所以四边形ADCN

为矩形．所以ANNB2.又因为AD2，AB4，所以AC，CN2，BC 所以AC2+BC2AB2，所以ACBC；………2分 因为AF平面ABCD，AF//BE

所以BE平面ABCD，所以BEAC，………3分 又因为BE平面BCE，BC平面BCE， BEBCB所以AC平面BCE．………4分 14

(Ⅱ) 因为AF平面ABCD，AF//BE,所以BE平面ABCD,VACDEVEACDEBSACD………8分

33

则所求概率为P(A)=

C （Ⅲ）存在，点M为线段EF中点，证明如下：…………9分

在矩形ABEF中，因为点M，N为线段AB的中点，所以四边形BEMN为正方形，所以BMEN；………10分

因为AF平面ABCD，AD平面ABCD，所以AFAD.在直角梯形ABCD中，ADAB，又AFABA，所以AD平面ABEF，又CN//AD，所以CN平面ABEF，又BM平面ABEF所以CNBM；…………12分 又 CN

ENN，所以BM平面ENC，又EC平面ENC，所以BMCE.…………14分

x2y219．（本小题共14分）（Ⅰ）由题意知, b2…1分 由ea…3分 椭圆方程为481．……4分

（Ⅱ）若存在满足条件的点N，坐标为（t，0），其中t为常数.由题意直线PQ的斜率不为0，直线PQ的方程可设为：

xmy1,



xmy1,(mR)…………5分 设P(x1,y1),Q(x2,y2),联立x2y2，

184

消去x 得：(12m2)y24my60,…………7分 16m224(12m2)0恒成立，

4m6y1y2

,yy=所以y1+y2=……8分 由知：……9分 ， PNMQNMk,kk+k012PNQNPNQN

12m212m2x1tx2t

yy2y1y2

即1，……………10分 展开整理得2my1y2(1t)(y1y2)0， 0，即

my11tmy21tx1tx2t

2m(6)4m(1t)

0,…………………12分 即

12m212m2

即m(t4)0，又m不恒为0，t=4.故满足条件的点N存在，坐标为(4,0)……14分

ax22x1

(x0)，…………2分 20．（本小题共13分）（Ⅰ）函数的定义域为(0,)，f(x)

x

12x1122

(1)1(1)1取最小值x1(x0)依题意f(x)0在(x0)时恒成立，则a在时恒成立，当时，2

xxx

1，a(,1].………… 4分

123123

（Ⅱ）已知条件等价于方程xxlnxb0在[1,4]上有两个不同的实根，设g(x)xxlnx,x[1,4]，

4242

(x2)(x1)

，x[1,2)时，g(x)0，x(2,4]时，g(x)0 g(x)

2x

g(x)ming(2)ln22,g(1)5,g(4)2ln22，………… 6分

4

315

2ln2(34ln4)0，得g(1)g(4),则b(ln22,]……………8分 444

1x

（Ⅲ）先证：当x0时，lnxx1.令h(x)lnxx1，h(x)，可证x(0,1)时h(x)单调递增，x(1,)

x

时h(x)单调递减，x1时h(x)max0.所以x0时，lnxx1.……9分 用以上结论，由an0,可得lnanan1. an1lnanan2an1an22an1，故an112(an1), ……10分

a1a1a1a1

2,0n12，…，022,相乘得0n2n1. ………12分 所以当n2时，0n

an11an21a11a11

由g(1)g(4)

又a11,故an12，即an21.…………13分 【注：若有其它解法，请酌情给分．】

n

n

2015石景山一模文科数学(四)
2015年石景山高三数学一模(文)试题及答案

石景山区2014—2015学年第一学期期末考试试卷

高三数学（文）

本试卷共6页，150分.考试时长120分钟.请务必将答案答在答题卡上，在试卷上作答无效.考试结束后上交答题卡.

第一部分（选择题 共40分）

一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题

目要求的一项．

1．设集合U1,2,3,4,A（CUA）B（ ） 1,2,B2,4 , 则

A.2 B.1,2,4 C.4 D.1,4 2．下列函数中，在(0，)上单调递增，并且是偶函数的是（ ）

A.yx B.yx C.ylg|x| D.y2 3．已知向量(2，4)，(0，2)，则

2

3

x

1

（ ） 2

A.(2，2) B.(2，2) C.(1,1) D.(1,1) 4．若某程序框图如右图所示，则该程序运行后

输出的B等于（ ）

A.63 B.31 C.15 D.7 5．设a,b为实数，命题甲：abb，

命题乙：ab0， 则命题甲是命题乙的（ ）

A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件

高三数学（文科）第1页（共14页）

2

6．函数fxlog2xx2的零点所在的区间是（ ）

A.（0，1） B.（1，2） C.（2，3） D.（3，4） 7．若点A(1,0)和点B(4,0)到直线l的距离依次为1和2，则这样的直线有（ ）

A.1条 B.2条 C.3条 D.4条

8．某同学为了研究函数f(x)x(1x)(0x1)的性质，构造了如图 所示的两个边长为1的正方形ABCD和BEFC，点P是边BC上的一个动点，设

2

2

CPx，则f(x)PF

AP．那么可推知方程f(x) ）

A.0 B.1 C.2 D.4

第二部分（非选择题 共110分）

二、填空题共6小题，每小题5分，共30分． 9. 若复数Z1i, Z23i,则

Z2

 . Z1

x2

y21的右焦点重合，10．若抛物线yax的焦点与双曲线则a的值为 ． 3

2

11．在ABC中，角A,B,C所对的边分别为a,b,c，已知C

则B____________．

12． 如图，网格纸上正方形的边长为1，粗实线

画出的是某多面体的三视图，则该多面体的 各条棱中，最长的棱的长度为 ．

高三数学（文科）第2页（共14页）



6

，a1，b3，

xy0，

13．已知不等式组xy0，表示的平面区域S的面积为1，则a ；

ya

若点P(x,y)S，则zx3y 的最小值为 . 14. 将连续整数1，2，…，25填入如图所示的5行5列的

表格中，使每一行的数从左到右都成递增数列，则第三列 各数之和的最小值为 ，最大值为 .

三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题共13分）

设数列an满足:a11,an13an,nN.

*

(Ⅰ)求数列an的通项公式及前n项和Sn；

(Ⅱ)已知数列bn是等差数列,Tn为bn的前n项和,且b1a1a2a3,b3a3, 求Tn的最大值.

高三数学（文科）第3页（共14页）

16．（本小题共13分）

已知函数f(x)Asin(x)(xR,0,0（Ⅰ）求函数f(x)的解析式；

（Ⅱ）求函数f(x)在区间[



2

）的部分图象如图所示.



2

,0]上的最大值与最小值.

高三数学（文科）第4页（共14页）

17．（本小题共14分）

如图所示，在正方体ABCDA1B1C1D1中，E、F分别是棱DD1、C1D1的中点． （Ⅰ）证明：平面ADC1B1平面A1BE； （Ⅱ）证明：B1F//平面A1BE；

A1

B1

1

（Ⅲ）若正方体棱长为1，求四面体A1B1BE的体积. B

高三数学（文科）第5页（共14页）1E

D

2015石景山一模文科数学(五)
2015年北京石景山高三一模数学(文科)试题及答案

2015年北京石景山高三一模数学（文科）试题及答案

石景山区2014—2015学年第一学期期末考试试卷

高三数学（文）

本试卷共6页，150分.考试时长120分钟.请务必将答案答在答题卡上，在试卷上作答无效.考试结束后上交答题卡.

第一部分（选择题 共40分）

一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目

要求的一项．

1．设集合U1,2,3,4,A（CUA）B（ ） 1,2,B2,4 , 则

A.2 B.1,2,4 C.4 D.1,4 2．下列函数中，在(0，)上单调递增，并且是偶函数的是（ ）

A.yx B.yx C.ylg|x| D.y2 3．已知向量(2，4)，(0，2)，则

2

3x

1

（ ） 2

A.(2，2) B.(2，2) C.(1,1) D.(1,1) 4．若某程序框图如右图所示，则该程序运行后

输出的B等于（ ）

A.63 B.31 C.15 D.7 5．设a,b为实数，命题甲：abb，

命题乙：ab0， 则命题甲是命题乙的（ ）

A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件

2

6．函数fxlog2xx2的零点所在的区间是（ ）

A.（0，1） B.（1，2） C.（2，3） D.（3，4） 7．若点A(1,0)和点B(4,0)到直线l的距离依次为1和2，则这样的直线有（ ）

A.1条 B.2条 C.3条 D.4条

8．某同学为了研究函数f(x)x(1x)(0x1)的性质，构造了如图 所示的两个边长为1的正方形ABCD和BEFC，点P是边BC上的一个动点，设

2

2

CPx，则f(x)PF

AP．那么可推知方程f(x) ）

A.0 B.1 C.2 D.4

第二部分（非选择题 共110分）

二、填空题共6小题，每小题5分，共30分． 9. 若复数Z1i, Z23i,则

Z2

 . Z1

x2

y21的右焦点重合，则a的值为 ． 10．若抛物线yax的焦点与双曲线3

2

11．在ABC中，角A,B,C所对的边分别为a,b,c，已知C

则B____________．

12． 如图，网格纸上正方形的边长为1，粗实线

画出的是某多面体的三视图，则该多面体的 各条棱中，最长的棱的长度为 ．



6

，a1，b，

xy0，

13．已知不等式组xy0，表示的平面区域S的面积为1，则a ；

ya

若点P(x,y)S，则zx3y 的最小值为 .

14. 将连续整数1，2，…，25填入如图所示的5行5列的

表格中，使每一行的数从左到右都成递增数列，则第三列 各数之和的最小值为 ，最大值为 .

三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题共13分）

设数列an满足:a11,an13an,nN.

*

(Ⅰ)求数列an的通项公式及前n项和Sn；

(Ⅱ)已知数列bn是等差数列,Tn为bn的前n项和,且b1a1a2a3,b3a3, 求Tn的最大值. 16．（本小题共13分）

已知函数f(x)Asin(x)(xR,0,0（Ⅰ）求函数f(x)的解析式；

（Ⅱ）求函数f(x)在区间[



2

）的部分图象如图所示.



2

,0]上的最大值与最小值.

17．（本小题共14分）

如图所示，在正方体ABCDA1B1C1D1中，E、F分别是棱DD1、C1D1的中点． （Ⅰ）证明：平面ADC1B1平面A1BE； （Ⅱ）证明：B1F//平面A1BE；

（Ⅲ）若正方体棱长为1，求四面体A1B1BE的体积.

B

D

B1

A1

1E 1

18．（本小题共13分）

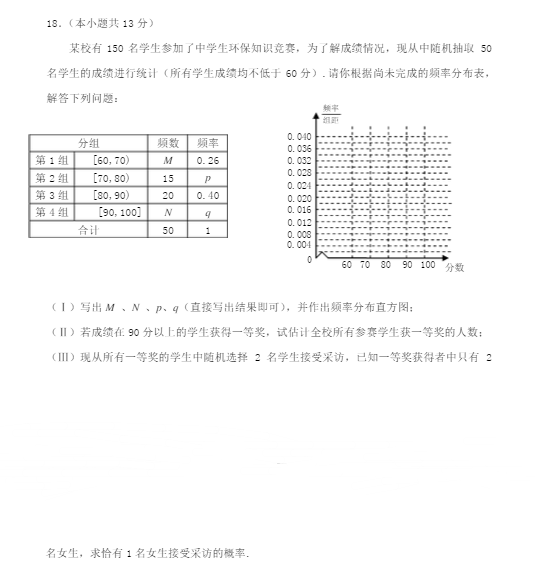
某校有150名学生参加了中学生环保知识竞赛，为了解成绩情况，现从中随机抽取50名学生的成绩进行统计（所有学生成绩均不低于60分）.请你根据尚未完成的频率分布表，解答下列问题：

（Ⅰ）写出M 、N 、p、q（直接写出结果即可），并作出频率分布直方图；

（Ⅱ）若成绩在90分以上的学生获得一等奖，试估计全校所有参赛学生获一等奖的人数； （Ⅲ）现从所有一等奖的学生中随机选择2名学生接受采访，已知一等奖获得者中只有2

本文来源：http://www.guakaob.com/gaozhong/524378.html