海淀区八年级第二学期期末练习数学

【www.guakaob.com--高一】

海淀区八年级第二学期期末练习数学(一)
2015.7海淀区八年级第二学期期末练习数学试题及答案word版

2015.7海淀区八年级第二学期期末练习数学

一、选择题：（本题共30分，每小题3分）在下列各题的四个备选答案中，只有一个是正确的． ．．．．1．一元二次方程3x24x50的二次项系数、一次项系数、常数项分别是

A．3,4,5 B．3,4,5 C．3,4,5 D．3,4,5 2

．函数y

x的取值范围是

D．x3

A．x3 B．x3 C．x3

3．下列各曲线表示的y与x的关系中，y不是．．x的函数的是

A．

B． C． D．

3，y1）4．已知P，P2（2，y2）是一次函数y2x1图象上的两个点，则y1，y2的大小关系是 1（

A．y1y2 B．y1y2 C．y1y2 D．不能确定 5．用配方法解方程x4x70时，原方程应变形为

A．x211 B．x211 C． x423 D．x423 6．本市5月份某一周每天的最高气温统计如下表：

2

2

2

2

2

则这组数据的中位数和平均数分别是 A．24，25

B．25，26

C．26，24

D．26，25

7．如图，在四边形ABCD中，对角线ACBD， 点E、F、G、H 分别为AB、BC、CD、DA的中点.若AC8，BD6，则四边形EFGH的面积为 A．14

B．12

C． 24

D． 48

8．如图，在菱形ABCD中，点M、N分别在AB、CD上， AM=CN，MN与AC交于点O，连接BO．若∠DAC=28°，则∠OBC为

A．28°

B．52°

C．62° D．72°

9．如图，直线y1xm与y2kxn相交于点A.若点A的横坐标为2，则下列结论中错误的是 ．．

A．k0

B．mn

C．当x2时，y2y1 D．2knm2 10．如图，若点P为函数ykxb(4x4)图象上的一动点，

m表

示点P到原点O的距离，则下列图象中，能表示m与点P的横坐标x的函数关系的图象大致是

A．

B．

C．

D．

二、填空题：（本题共18分，每小题3分）

11．在□ABCD中，若∠B=50°，则∠C．

12．将直线y2x3向上平移4个单位长度得到的直线的解析式为

2

13．若关于x的方程9x6xm0有两个相等的实数根，则m

14．某通讯公司的4G上网套餐每月上网费用y (单位：元) 与上网流量x（单位：兆）的函数关系的图象如图所示.若 该公司用户月上网流量超过500兆以后，每兆流量的费用为 0.29元，则图中a的值为．

15．用两个全等的直角三角形无缝隙不重叠地拼下列图形：

①矩形；②菱形；③正方形；④等腰三角形；⑤等边三角形，一定能够拼成的图形是 ．． （填序号）.

16．边长为a的菱形是由边长为a的正方形 “形变”得到的，若这个菱形一组对边之间的 距离为h，则称

a

为这个菱形的“形变度”． h

（1）一个“形变度”为3的菱形与其“形变”前的正方形的面积之比

为 ；

（2）如图，A、B、C为菱形网格（每个小菱形的边长为1， 9

“形变度”为）中的格点，则△ABC的面积为 ．

8

三、解答题：（本题共22分，第17题4分，第18题8分，第19题5分，第20题5分） 17【海淀区八年级第二学期期末练习数学】

．计算：解：

18．（1）解方程：x(x1)22x． 解：

（2）若x1是方程x4mx2m0的一个根，求代数式3m11的值．

2

2

2

解：

19．如图，E、F是□ABCD对角线AC上的两点，AF=CE.求证：BE=DF． 证明：

20．在平面直角坐标系xOy中，一次函数的图象经过点A（1，-3）和B（2，0）． （1）求这个一次函数的解析式；

（2）若以O、A、B、C为顶点的四边形为菱形，则点C的坐标为 （直接写出答案）． 解：

四、解答题：（本题共10分，第21题5分，第22题5分）

21. 如图，菱形ABCD的对角线AC、BD相交于点O，DE∥AC，DE=

ABC60，求AE的长.

1

AC，连接AE、CE.若AB=2，2

解：

22．列方程解应用题：

随着经济的增长和人民生活水平的提高，我国公民出境旅游人数逐年上升．据统计， 2012年我国公民出境旅游总人数约为8000万人次， 2014年约为11520万人次，求我国公民出境旅游总人数的年平均增长率． 解：

五、解答题：（本题共20分，第23题6分，第24题7分，第25题7分）

23．如图，在□ABCD中，对角线AC、BD相交于点O，点E为点B关于直线AC的对称点，连接EB、ED.

（1）求BED的度数；

（2）过点B作BE的垂线交EA的延长线于点F，请补全图形，并证明DEACBF. 解：

海淀区八年级第二学期期末练习数学(二)
海淀区2014—2015学年度第二学期八年级期末考试数学

海淀区2014—2015学年度第二学期八年级期末考试

数 学 试 卷 2015月6月

一、选择题（本题共24分，每小题3分）

下面各题均有四个选项，其中只有一个是符合题意的，请将正确答案前的字母填入下面的答题表中． ．．．． ( )1．抛物线y=2（x﹣3）2+1的顶点坐标是（ ）

( )2、已知

，那么

的值为( )

A．-l B．1 C．32007 D．

( )3．已知一次函数ykx1，y随x的增大而减小，则该函数的图象一定经过

A．第一、二、三象限 B．第一、二、四象限 C．第一、三、四象限 D．第二、三、四象限

( )4．已知x2是一元二次方程x22ax80的一个根，则a的值为 A．1 B．－1 C．3 D．－3

( )5．将抛物线y4x2向左平移1个单位，再向下平移3个单位后所得抛物线的解析式为 A．y4x13 C．y4x13

22

B．y4x13 D．y4x－13

2

2

( )6．某学习小组7位同学，为玉树地震灾区捐款，捐款金额分别为510元，6元，6元，

7元，8元，9元，则这组数据的中位数与众数分别为（ ）

A．6，6 B．7，6 C．7，8 D．6，8

( )7．如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，

∠BED=150°，则∠A的大小为

A．150°

B．130° C．120° D．100°

( )8．如图，正方形ABCD的边长为4cm，动点P、Q同时从点A出发，以1cm/s的速度分别沿A→B→C 和A→D→C的路径向点C运动，设运动时间为x（单位：s），四边形PBDQ的面积为y（单位：cm2），则y与x（0≤x≤8）之间的函数图象大致是

A． B． C． D． 二、填空题（本题共16分，每小题4分） 9．如果二次根式

有意义，则x的取值范围是 ．

10．如图，在直角三角形ABC中，∠C=90°，AB=10，AC=8， 点E、F分别为AC和AB的中点，则EF= ．

11．某一型号的飞机着陆后滑行的距离S（单位：m）与滑行时间t（单位：s）之间的函数关系式是

S60t1.5t2，则该型号飞机着陆后滑行才能停下来．

12．方程4x(x-1)=2(x+2)+8化成一般形式是____________________,二次项系数是 ,一次项系数是 ,常数项是 .

三、解答题（本题共26分．第13题～14题，每题各3分；第15题～18题，每题各5分） 13

14．解方程：x26x3．

15．已知：如图，AB= AC，∠DAC=∠EAB，∠B=∠C．

求证：BD= CE．

证明：

16．已知xx20，求代数式x(2x1)(x1)(x1)的值

2

17．列方程解应用题：

“美化城市，改善人民居住环境”是城市建设的一项重要内容．某市近年来，通过植草、栽树、修建公园等措施，使城区绿地面积不断增加，2011年底该市城区绿地总面积约为75公顷，截止到2013年底，该市城区绿地总面积约为108公顷，求从2011年底至2013年底该市城区绿地总面积的年平均增长率．

18．若关于x的一元二次方程kx4x30有实根． （1）求k的取值范围；

（2）当k取得最大整数值时，求此时方程的根．【海淀区八年级第二学期期末练习数学】

2

四、解答题（本题共20分，每题各5分） 19．已知二次函数y＝2x24x．

（1）将此函数解析式用配方法化成y＝a(x－h)2k的形式；

（2）在给出的直角坐标系中画出此函数的图象（不要求列对应数值表，但要求尽可能画准确）； （3）当0<x<3时，观察图象直接写出函数值y的取值范围：．

20．如图，在□ABCD中，对角线AC，BD相交于点O，且OA＝OB． （1）求证：四边形ABCD是矩形；

（2）若AD＝4，∠AOD＝60°，求AB的长．

A

B

21.下表是某校八年级（1）班20名学生某次数学测验的成绩统计表

（1）若这20名学生成绩的平均分数为82分，求x和y的值；

（2）在（1）的条件下，设这20名学生本次测验成绩的众数为a，中位数为b，求a，b的值．【海淀区八年级第二学期期末练习数学】

22． 如图，在平面直角坐标系xOy中，正比例函数y=x的图象与一次函数y=kx－k的图象的交点坐标

为A（m，2）．

（1）求m的值和一次函数的解析式；

（2）设一次函数y=kx－k的图象与y轴交于点B，求△AOB的面积；

（3）直接写出使函数y=kx－k的值大于函数y=x的值的自变量x的取值范围．

五、解答题（本题共14分，每题各7分）

23．已知抛物线y＝12x2mx2m7

2

的顶点为点C．

（1）求证：不论m为何实数，该抛物线与x轴总有两个不同的交点； （2）若抛物线的对称轴为直线x＝3，求m的值和C点坐标； （3）如图，直线y＝x1与（2）中的抛物线交于A、B两点，并与它的

对称轴交于点D．直线x＝k交直线AB于点M，交抛物线于点N．求当k为何值时，以C，D，M，N为顶点的四边形是平行四边形．

海淀区八年级第二学期期末练习数学(三)
2014-2015学年北京市海淀区八年级第二学期期末数学试题

海淀区八年级2014-2015学年第二学期期末数学练习 2015.7

一、选择题：（本题共30分，每小题3分）

1．一元二次方程3x24x50的二次项系数、一次项系数、常数项分别是（ ）

A．3,4,5 B．3,4,5 C．3,4,5 D．3,4,5

2

．函数yx的取值范围是（ ）

D．x3 A．x3 B．x3 C．x3

3．下列各曲线表示的y与x的关系中，y不是．．x的函数的是（ ）

4．已知P1（3，y1），P2（2，y2）是一次函数y2x1图象上的两个点，则y1，y2的大小关系是（ ）

A．y1y2 B．y1y2 C．y1y2 D．不能确定

25．用配方法解方程x4x70时，原方程应变形为（ ）

A．x211 B．x211 C． x423 D．x423

6．本市5月份某一周每天的最高气温统计如下表：

2222

则这组数据的中位数和平均数分别是（ ）

A．24，25

7．如图，在四边形ABCD中，对角线ACBD， 点E、F、G、H分别为AB、BC、CD、DA的中点.若AC8，BD6，则四边形EFGH的面积为（ ）

A．14 B．12 C． 24 D． 48

B．25，26 C．26，24 D．26，25

8．如图，在菱形ABCD中，点M、N分别在AB、CD上， AM=CN，MN与AC交于点O，连接BO．若∠DAC=28°，则∠OBC为（ ）

A．28° B．52° C．62° D．72°

9．如图，直线y1xm与y2kxn相交于点A.若点A的横坐标为2，则下列结论中错误的是（ ） ．．

A．k0 B．mn

C．当x2时，y2y1 D．2knm2

10．如图，若点P为函数ykxb(4x4)图象上的一动点， m表示点P到原点O的距离，则下列图象中，能表示m与点P的横坐标x的函数关系的图象大致是（ ）

二、填空题：（本题共18分，每小题3分）

11．在□ABCD中，若∠B=50°，则∠C．

12．将直线y2x3向上平移4个单位长度得到的直线的解析式为．

13．若关于x的方程9x6xm0有两个相等的实数根，则m．

14．某通讯公司的4G上网套餐每月上网费用y (单位：元)

与上网流量x（单位：兆）的函数关系的图象如图所示.若

该公司用户月上网流量超过500兆以后，每兆流量的费用为

0.29元，则图中a的值为

15．用两个全等的直角三角形无缝隙不重叠地拼下列图形：

①矩形；②菱形；③正方形；④等腰三角形；⑤等边三角形，一定能够拼成的图形是 （填序号）. ．．

2

16．边长为a的菱形是由边长为a的正方形 “形变”得到的，若这个菱形一组对边之间的

a距离为h，则称为这个菱形的“形变度”． h

（1）一个“形变度”为3的菱形与其“形变”前的正方形的面积之比

为 ；

（2）如图，A、B、C为菱形网格（每个小菱形的边长为1， 9“形变度”为）中的格点，则△ABC的面积为 ． 8

三、解答题：（本题共22分，第17题4分，第18题8分，第19题5分，第20题5分）

17

．计算：

18．（1）解方程：x(x1)22x．

22（2）若x1是方程x4mx2m0的一个根，求代数式3m11的值． 2

19．如图，E、F是□ABCD对角线AC上的两点，AF=CE.求证：BE=DF．

20．在平面直角坐标系xOy中，一次函数的图象经过点A（1，-3）和B（2，0）．

（1）求这个一次函数的解析式；

（2）若以O、A、B、C为顶点的四边形为菱形，则点C的坐标为 （直接写出答案）．

四、解答题：（本题共10分，第21题5分，第22题5分）

21. 如图，菱形ABCD的对角线AC、BD相交于点O，DE∥AC，DE=

ABC60，求AE的长. 1AC，连接AE、CE.若AB=2，2

22．列方程解应用题：

随着经济的增长和人民生活水平的提高，我国公民出境旅游人数逐年上升．据统计， 2012年我国公民出境旅游总人数约为8000万人次， 2014年约为11520万人次，求我国公民出境旅游总人数的年平均增长率．

五、解答题：（本题共20分，第23题6分，第24题7分，第25题7分）

23．如图，在□ABCD中，对角线AC、BD相交于点O，点E为点B关于直线AC的对称点，连接EB、ED.

（1）求BED的度数；

（2）过点B作BE的垂线交EA的延长线于点F，请补全图形，并证明DEACBF.

24．已知：关于x的方程mx2(3m1)x2m20(m1)．

（1）求证：方程有两个不相等的实数根；

（2）设方程的两个实数根分别为x1，x2（其中x1x2），若y是关于m的函数，且ymx22x1， 求这个函数的解析式；

（3）将（2）中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折，图象的其余部分保持不变，

得到一个新的图象．请你结合这个新的图象回答：当关于m的函数y2mb的图象与此图象有两个公共点时，b的取值范围是 （直接写出答案）．

海淀区八年级第二学期期末练习数学(四)
海淀区八年级2014-2015学年第二学期期末练习

海淀区八年级2014-2015学年第二学期期末练习

数 学

（分数：100分 时间：90分钟） 2015.7

学校 班级 姓名 成绩

一、选择题：（本题共30分，每小题3分）

在下列各题的四个备选答案中，只有一个是正确的． ．．．．

1．一元二次方程3x24x50的二次项系数、一次项系数、常数项分别是

A．3,4,5 B．3,4,5 C．3,4,5 D．3,4,5

2

．函数yx的取值范围是

D．x3 A．x3 B．x3 C．x3

3．下列各曲线表示的y与x的关系中，y不是．．x的函数的是

A．

B． C． D．

4．已知P1（3，y1），P2（2，y2）是一次函数y2x1图象上的两个点，则y1，y2的大小关系是

A．y1y2 B．y1y2 C．y1y2 D．不能确定

25．用配方法解方程x4x70时，原方程应变形为

A．x211 B．x211 C． x423 D．x423

2222

6．本市5月份某一周每天的最高气温统计如下表：

则这组数据的中位数和平均数分别是

A．24，25 B．25，26 C．26，24 D．26，25

7．如图，在四边形ABCD中，对角线ACBD， 点E、F、G、H

分别为AB、BC、CD、DA的中点.若AC8，BD6，则四边形

EFGH的面积为

A．14 B．12 C． 24 D． 48

8．如图，在菱形ABCD中，点M、N分别在AB、CD上， AM=CN，

MN与AC交于点O，连接BO．若∠DAC=28°，则∠OBC为

A．28° B．52° C．62° D．72°

9．如图，直线y1xm与y2kxn相交于点A.若点A的横坐

标为2，则下列结论中错误的是 ．．

A．k0 B．mn

C

．当x

2

时，y2y1 D．2knm2

10．如图，若点P为函数ykxb(4x4)图象上的一动点，

m表示点P到原点O的距离，则下列图象中，能表示

m

与点

P

的横

坐标x的函数关系的图象大致是

A．

D． B． C．

二、填空题：（本题共18分，每小题3分）

11．在□ABCD中，若∠B=50°，则∠C°．

12．将直线y2x3向上平移4个单位长度得到的直线的解析式为．

213．若关于x的方程9x6xm0有两个相等的实数根，则m

14．某通讯公司的4G上网套餐每月上网费用y (单位：元)

与上网流量x（单位：兆）的函数关系的图象如图所示.若

该公司用户月上网流量超过500兆以后，每兆流量的费用为

0.29元，则图中a的值为

15．用两个全等的直角三角形无缝隙不重叠地拼下列图形：

①矩形；②菱形；③正方形；④等腰三角形；⑤等边三角形，一定能够拼成的图形是 ．．

（填序号）.

16．边长为a的菱形是由边长为a的正方形 “形变”得到的，若这个菱形一组对边之间的 距离为h，则称a为这个菱形的“形变度”． h

（1）一个“形变度”为3的菱形与其“形变”前的正方形的面积

之比为 ；

（2）如图，A、B、C为菱形网格（每个小菱形的边长为1， 9“形变度”为）中的格点，则△ABC的面积为 ． 8

三、解答题：（本题共22分，第17题4分，第18题8分，第19题5分，第20题5分）

17

．计算：解：

18．（1）解方程：x(x1)22x．

解：

22（2）若x1是方程x4mx2m0的一个根，求代数式3m11的值． 2

解：

19．如图，E、F是□ABCD对角线AC上的两点，AF=CE.

求证：BE=DF．

证明：

20．在平面直角坐标系xOy中，一次函数的图象经过点A（1，-3）和B（2，0）．

（1）求这个一次函数的解析式；

（2）若以O、A、B、C为顶点的四边形为菱形，则点C的坐标为 （直接写出答案）． 解：

四、解答题：（本题共10分，第21题5分，第22题5分）

21. 如图，菱形ABCD的对角线AC、BD相交于点O，DE∥AC，DE=

CE.若AB=2，ABC60，求AE的长.

解：

1AC，连接AE、2

海淀区八年级第二学期期末练习数学(五)
2015海淀区数学八年级第一学期期末练习

海淀区八年级第一学期期末练习

数 学 2015.1

（分数：100分 时间：90分钟）

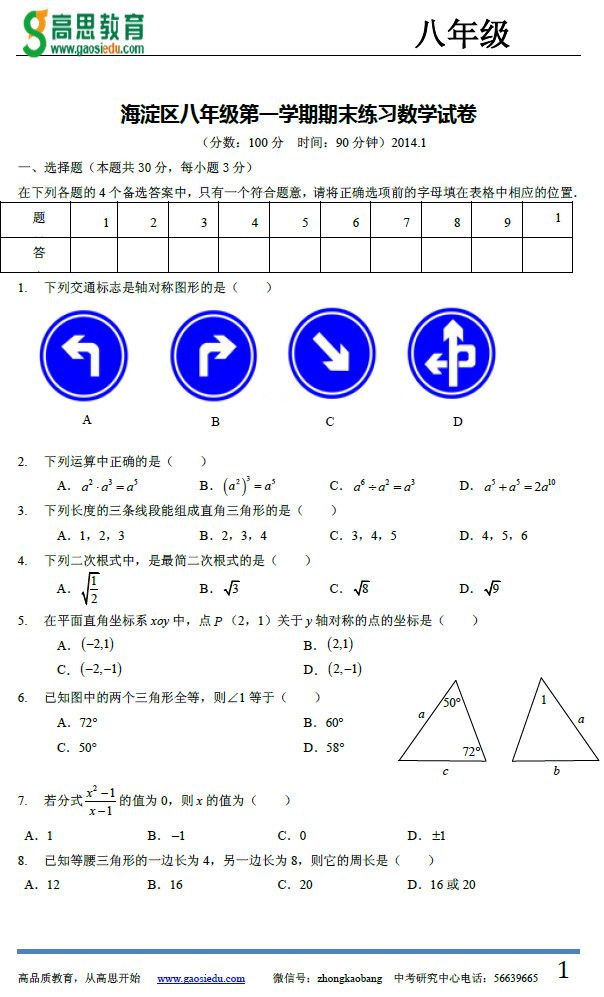
学校 班级 姓名 成绩 一、选择题：（本题共36分，每小题3分）

在下列各题的四个备选答案中，只有一个是正确的. 请将正确选项前的字母填在表格中相应的位置.

．．

（A） （B） （C） （D

） 2．下列运算中正确的是

（A）2x3y5xy （B）x8x2x4

2363

（C）(xy)xy （D）2x3x22x6

3．在平面直角坐标系xOy中，点P（－3，5）关于x轴的对称点的坐标是

（A） （3，5） （B）（3，－5） （C）（5，－3） （D）（－3，－5） 4x的取值范围是 （A）x ≠－

2223

（B）x<－

（C）x≥－

（D）x≥



2333

5．下列各式中，从左到右的变形是因式分解的是

（A）3x3y53(xy)5 （B）(x1)(x1)x21 （C）x22x1(x1)2 （D）x(xy)x2xy 6．下列三个长度的线段能组成直角三角形的是

（A）1 （B）1 （C）2，4，6 （D）5，5，6 7．计算2(3) ，结果为

（A）6 （B）6 （C）66 （D）66

8．下列各式中，正确的是 （A）

bb2b1

（B） 

a2ba2aa2

ababa2a24

（C） （D） 

a2(a2)2cc

9．若xm与2x的乘积中不含x的一次项，则实数m的值为 （A）2 （B）2 （C）0 （D）1

10.如图，在△ABC和△CDE中，若ACBCED90,AB=CD，BC=DE，则下列结论中不正确的是 ．．．

（A）△ABC ≌ △CDE （B）CE=AC （C）AB⊥CD （D）E为BC中点

11．如图，由四个全等的直角三角形与一个小正方形拼成一个大正方形. 如果大正方形的面积是25，小正方形的面积是1，直角三角形的两条直角边的长分别是a和

b，那么(ab)2的值为

（A）49 （B）25 （C）13 （D）1

11111

12.当x分别取2014、2013、2012、….、2、1、0、1、、、…、、、

23201220132014

x21

时，计算分式2的值，再将所得结果相加，其和等于

x1

（A）1 （B）1 （C）0 （D） 2014 二、填空题:（本题共24分，每小题3分）

13．若实数x、

yy20，则xy的值为2b

14．计算：3

5a

15

．比较大小：.

16．分解因式：3a312a=

17．如图，△ABC≌△DEF，点F在BC边上，AB与EF相交于点P.若DEF37，PB=PF，则APF °. 18．如图，△ABC是等边三角形，点D为 AC边上一点，以BD为边作等边△BDE, 连接CE．若CD＝1，CE＝3，则BC＝_____． 19．在平面直角坐标系xOy中，点A、点B的坐标分别为（－6，

0）、（0，8）．若△ABC是以∠BAC为顶角的等腰三角形，点C在x轴上，则点C的坐标为 ．

2

20.如图，分别以正方形ABCD的四条边为边，向其内部作等边三角形，得到△ABE、△BCF、△CDG、△DAH，连接EF、FG、GH、HE.若AB=2，则四边形EFGH的面积为 . 三、解答题：（本题共14分，第21题5分，第22题9分） 21．计算：

22．（1）解方程：

1

()1(

2)0+．

2

x2

1. x1x

xx24x4x

)（2））先化简，再求值：(，其中x2. 2

x2x2x4

四、解答题：（本题共9分，第23题4分,第24题5分）

23.如图，点F、C在BE上，BFCE，ABDE，∠B=∠E. 求证: ∠A=∠D.

24. 列方程(组)解应用题

:

上图为地铁调价后的计价图. 调价后，小明、小伟从家到学校乘地铁分别需4元和3元.由于刷卡坐地铁有优惠，因此，他们平均每次实付3.6元和2.9元.已知小明从家到学校乘地铁的里程比小伟从家到学校乘地铁的里程多5千米，且小明每千米享受的优惠金额是小伟的2倍，求小明和小伟从家到学校乘地铁的里程分别是多少千米？

五、解答题：（本题共17分，第25题5分，第26题6分，第27题6分） 25．已知：如图，△ABC，射线AM平分BAC. （1）尺规作图（不写作法，保留作图痕迹）

作BC的中垂线，与AM相交于点G，连接BG、CG. （2）在（1）的条件下，∠BAC和∠BGC的等量关系为 ，证明你的结论.

26．阅读：

对于两个不等的非零实数a、b，若分式

(xa)(xb)

的值为零，则xa或xb.又因为

x

(xa)(xb)x2(ab)xababab

ab有两个解，x(ab)，所以关于x的方程xxxxx

分别为x1a，x2b.

应用上面的结论解答下列问题： （1）方程x

8

6的两个解中较大的一个为； x

（2）关于x的方程x

mnm4mnn

的两个解分别为x1、x2（x1x2），若x1与x2互为倒mnx2mn

数，则x1_____，x2______；

n22n3x2

2n3的两个解分别为x1、x2（x1x2）（3）关于x的方程2x，求2的值.

2x12x1

27.阅读：

如图1，在△ABC中，3AB180，BC4，AC5，求AB的长. 小明的思路：

如图2，作BEAC于点E，在AC的延长线上取点D，使得DEAE，连接BD,易得AD,△ABD为等腰三角形.由3AABC180和AABCBCA180，易得BCA2A，△BCD为等腰三角形.依据已知条件可得AE和AB的长.

图1 图2

解决下列问题：

（1）图2中， AE= ，AB= ；

（2）在△ABC中，A、B、C的对边分别为a、b、c.

①如图3，当3A2B180时，用含a、c的式子表示b；（要求写解答过程） ②当3A4B180，b2，c3时，可得a= .

图3

本文来源：http://www.guakaob.com/gaozhong/641136.html