【www.guakaob.com--高三】
淮南,位于安徽省中北部,地处长江三角洲腹地,淮河之滨,素有“中州咽喉,江南屏障”、“五彩淮南”之称,是沿淮城市群的重要节点,合肥经济圈成员之一。以下是中国招生考试网www.chinazhaokao.com 分享的淮南高三数学一模考试 淮南高三理综一模考试,希望能帮助到大家!
图1
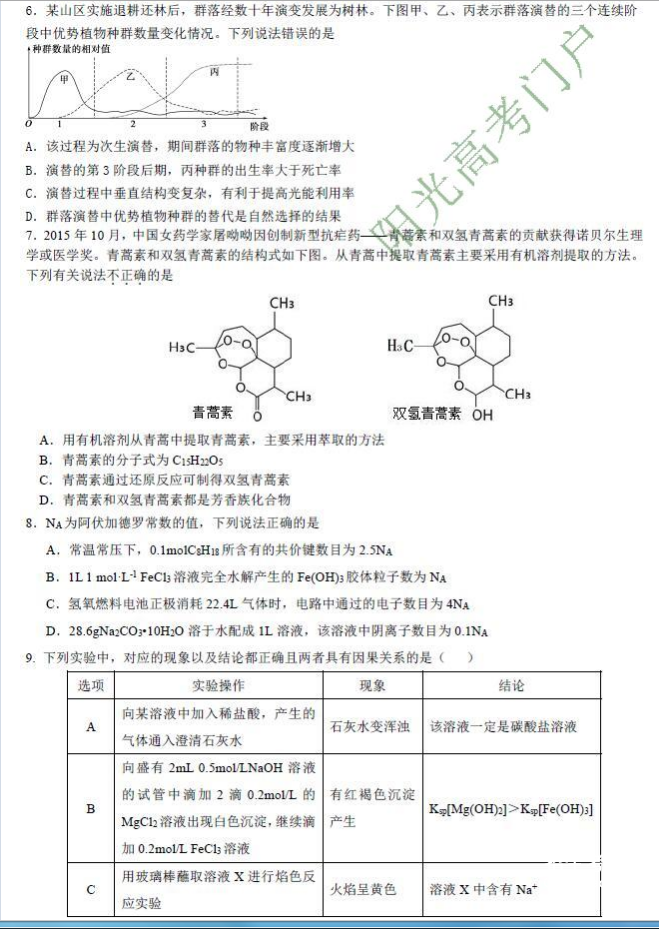
图2

图3
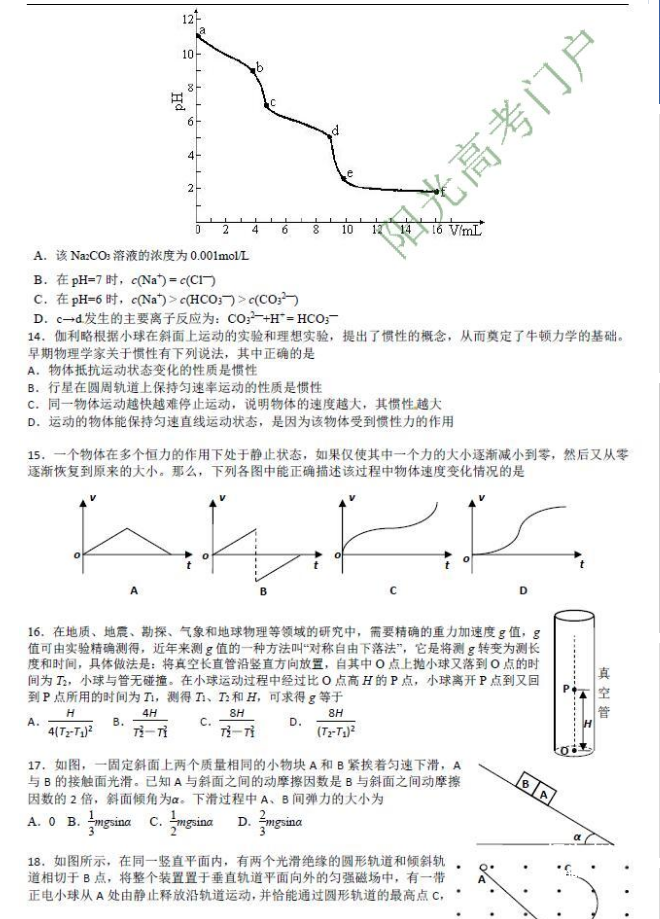
图4

图5
1. C 2. A 3. D 4. A 5. D 6.A.
7.A 8.B 9. D 10. A 11. D 12. D
13. (-∞,-2] 或-3, 16. 答:< .
17. 解:在△ABC中,根据==,得AB=·sinC=sinC=2sinC,同理BC=2sinA,因此AB+BC=2sinC+sinA .......................................... 4分
=2sinC+sin(π-C)=,因此AB+BC的最大值为.△ABC是等边三角形............................................................ 12分
18.解: (1)设{an}的公差为d.由题意,a=a1a13,
即(a1+10d)2=a1(a1+12d),
于是d(2a1+25d)=0.
又a1=25,所以d=0(舍去),或d=-2.
故an=-2n+27.
(2)令Sn=a1+a4+a7+…+a3n-2.
由(1)知a3n-2=-6n+31,故{a3n-2}是首项为25,公差为-6的等差数列.从而Sn=(a1+a3n-2)=·(-6n+56)=-3n2+28n.
19.(1)证明:在中,,
,......................................................................................................... 2分
又且、AC是面内的两条相交直线,
平面,又平面,
;.......................................................................................................... 4分
(2)在中,,,又且AB、AC是面ABC内的两条相交直线,面ABC,................................................. 8分
由(1)知,,,
,设点B到面的距离为,
由得,,解得,
点B到面的距离为....................................................................... 12分
用其它方法可参考给分.
20.(1)设M的坐标为,的坐标为
由已知得......................................................................................................... 2分
在圆上,即C的方程为.................................... 4分
(2)过点(3,0)且斜率为 的直线方程为,设直线与C的交点为
,将直线方程代入C的方程,得,
即...................................................................................................... 8分
.
................................................................................................ 12分
21.解:(1)
当时,........................................................................ 2分
令,则................................................. 4分
时>0;时<0.
,即(只在处取等号)
的单减区间是;............................................................................ 6分
(2),
令,则且函数在处的切线为,....................................................................................................................... 8分
由(1)知,时, 在上单减且,
,合题意.
当>时,数形结合知,在上仍单减且,
................................................................................................ 11分
综上:若且,恒有................................................... 12分
22.解析 (1)f(x)=sin(2x-2φ)-+=sin(2x-2φ)-cos(2x-2φ)=sin(2x-2φ-).
∵函数f(x)为偶函数,2φ+=kπ+,kZ.
∴φ=+,kZ.又0≤φ≤,φ=.
f(x)=sin(2x--)=-cos2x.
∴f(x)的最小正周期为T=.
由≤2x≤,kZ,得-≤x≤,kZ.
∴f(x)的单调减区间为[-,](kZ).
(2)函数f(x)=-cos2x的图像向右平移个单位,得到g(x)=-cos2(x-)的图像,即g(x)=-cos(2x-).
令2x-=+,kZ,,kZ.
∴g(x)的对称中心为(,0),kZ. ......................................................... 10分
23.解:<2-2<<10,............................................................ 2分
记-2<<10,B<0,
由题知,B , ... A............................................................................................. 4分
记,则
即
解此不等式组得,........................................................................... 8分
经检验时上等式组中两不等式的等号不同时成立.
∴的取值范围是………….......................................................... 10分
24.解:(1)∵++=,又++=(1-x,1-y)+(2-x,3-y)+(3-x,2-y)=(6-3x,6-3y),解得即=(2,2),故|=2(2)∵=m+n,(x,y)=(m+2n,2m+n),
两式相减得,m-n=y-x,令y-x=t,由图知,当直线y=x+t过点B(2,3)时,t取得最大值1,故m-n的最大值为1.