【www.guakaob.com--质量工程师】
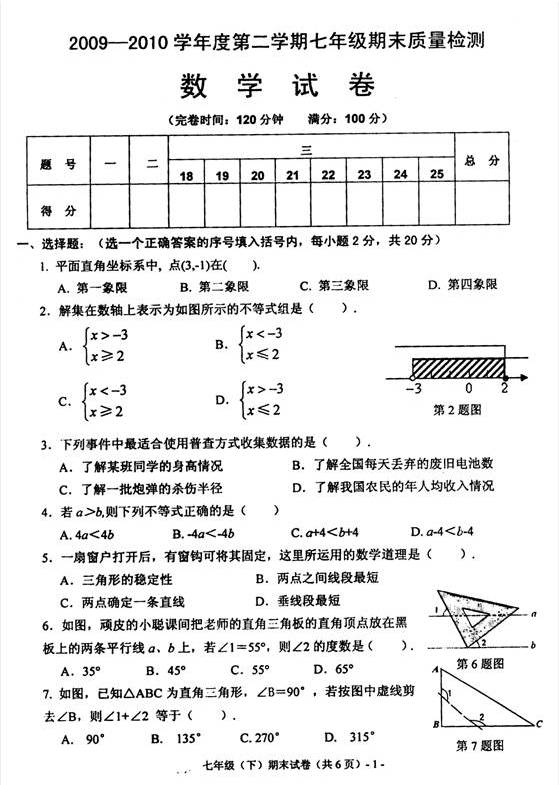
C
2013--2014学年度八年级数学第二学期期末质量检测试卷
(本大题共10个小题;每小题2分,共20分.在每小题给出一、你一定能选对!
的四个选项中,只有一项是符合题目要求的)
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
A
P
B
B
C
D
8某次考试,5名学生的平均分是82,除学生甲外,其余4名学生的平均分是80,那么学生甲的得分是( )
2-xm
2.如果关于x的方程无解,那么m的值为( )
x-55-xA.-2
B.5
C.2
D.3
x【龙岗区2015-2016学年第二学期期末质量监测试题八年级数学】
3.函数y=x的取值范围是( )
1-
x
A.x≠0 B.x≠1 C.x>1 D.x
<1且x≠0 4.菱形具有但矩形不具有的性质是( ) A.四边都相等 B.对边相等 C.对角线互相平分 D.对角相等
5
.如图,已知函数y=kx+b和y=kx的图像交于点P,则根据图像可得关于x,y的二元一次方程组的解是( )
A
..
A.84 B.86 C.88 D.90【龙岗区2015-2016学年第二学期期末质量监测试题八年级数学】
9.如图,在△ABC中,已知∠ABC和∠ACB的角平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E,若BD+CE=9,则DE的长为( )

A.9 B.8
C.7 D.6
10“五一”期间,几名同学租一辆面包前去旅游,面包车的租价为80元,出发时,又增加了两名同学,结果每名同学比原来少分摊了3元车费,若设参加旅游的学生总数共有x人,则依题意所列方程为( )
C.
6.依次连接等腰梯形各边中点所得到的四边形是( ) A.梯形 B.菱形 C.矩形 D.正方形
7.如图,矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A→B→C→M运动,则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的( )
1
180
x180
C、A、180180180
3 B、3 x2x2x180180180
3 D、3 2x2x
二、你能填得又快又准吗?(每小题3分,共计24分)
11.点M(a,2)是一次函数y=2x-3图像上的一点,则a=________.
12.一个多边形的内角和和它外角和相等,那么这个多边形是______边形。. 13.如图,若使菱形ABCD是正方形,则需添加的条件是________________(填上一个符合题目要求的条件即可)
14.甲、乙两名同学10次跳远的平均数相同,若甲10次立 定 跳远成绩的方差S甲=0.006,乙10次立定跳远的方差S乙=0.035,则成绩较为稳定的是_________(填“甲”或“乙”)
15..如图,在△ABC中,∠BAC=120,如果PM、QN分别垂直平分AB、AC,那么∠PAQ=_______,若BC=10cm,则△APQ的周长为____________. 16..如果一次函数y=(k+1)x-1的y随x的增大而增大,那么k的取值范围是 .
17.“平行四边形的对角线互相平分”的逆命题是_______________________
18.请写等腰梯形ABCD(AB//CD)具有而一般梯形不具有的三个特征:
三、好了,我们该做解答题了,相信你,能通过认真细致的思考,顺利地解答出这几个问题.(本大题共8小题,共计56分)
19.计算(5分)【龙岗区2015-2016学年第二学期期末质量监测试题八年级数学】
解分式方程
20(本小题满分7分)甲开车从距离B市100千米的A市出发去B市,乙从同一
路线上的C市出发也去往B。市,二人离A市的距离与行驶时间的函数图像如图所
示(y代表距离,x代表时间) (1)C市离A市的距离是_________千米; (2)甲的速度是________千米∕小时,乙的速度是___________千米∕小时; (3)________小时,甲追上乙;
(4)试分别写出甲、乙离开A市的距离y(千米)与行驶时间x(时)之间的函数关系式。(冀教八年级数学学习点睛P26)
2
2
2
21(本小题6分)如图,已知在四边形ABCD中,AB=CD,BC=AD,E、F是对角线AC
上两点,且AE=CF.求证:BE=DF
22.(本小题满分6分)已知一次函数的图像经过点(1,1)和(-1,-5)。
(1)求这个一次函数的表达式;
(2)求这个一次函数的图像与x轴、y轴的交点坐标,并求出该图像与两坐标轴围成的三角形
的面积。
1x
2 x33x
23.(本小题10分)
2009年8月8日我国台湾省遭受了50年罕见的“莫拉克”台风风暴。灾情牵
动着大陆人民的心。“水灾无情人有情,我们都是中国人”。某市立即组织了20辆汽车装运食品、药品、生活用品三种救灾物资共100吨到灾民安置点。按计划20辆汽车都要装运,每辆汽车只能装运同一种救灾物资且必须装满。根据下表提供的信息,解答下列问题:
(2)如果装运食品的车辆数不少于5辆,装运药品的车辆数不少于4辆,那么,车辆的安排有几种方案?并写出每种安排方案。
(3)在(2)的条件下,若要求总运费最少,应采用哪种方案?并求出最少总运费。
24.(本小题满分6分)如图,在△ABC中,
∠ABC=45,AD⊥BC于点D,点E在AD上,且
BE=AC,观察并猜想线段DE与线段CD的大小关系,然后证明
3
25.(本小题满分8分)
为了迎接国庆60周年,提高中学生的爱国主义热情,我校特组织了以“唱爱
国歌曲,颂革命精神”为主题的歌咏比赛活动,中学部三个年级根据初赛成绩分别选出了10名同学
(1) 请你填写下表:
(2) 请从以下两个不同的角度对三个年级的决赛成绩进行分析:
① 从平均数和众数相结合看(分析哪个年级成绩好些) ② 从平均数和中位数相结合看(分析哪个年级成绩好些)
(
3) 如果在每个年级参加决赛的选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一
些?请说明理由。
26(本小题满分8分)如图,直线AC∥BD,连接AB,直线AC、BD及线段AB把平
面分成①、②、③、④四个部分,规定:线上各点不属于任何部分。当动点P落
在某个部分时,连接PA、PB,构成∠PAC,∠APB∠PBD三个角。(提示:有公共端点的两条重合的射
线所组成的角是0角)
(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD。
(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立(直接回答成立或不成立)? ____________
(3)当动点P落在第③部分时,全面探究∠PAC,∠APB,∠PBD之间的关系,并写出动点P的具体位置和相应的结论。选择其中一种结论加以证明。
4
参考答案
一、你一定能选对!
二、你能填得又快又准吗?
115
2
.四边形 13.∠BAD=90或AO=BO或AC=BD 14.甲 15.60,10
16.K>-1, 17.对角线互相平分的四边形是平行四边形 18.两腰相等,同一底上两角相等,对角线相等 三、
19.解:去分母得1=2(x-3)-x „„„„„„„„„„„„„„„„„3分 去括号得1=2x-6-x
解得 x=7 „„„„„„„„„„„„„„„„„„4分 经检验x=7是原方程的解
所以原方程的解是x=7 „„„„„„„„„„„„„„„„„„5分 20.(1)28 „„„„„„„„„„„„„„„„„„„„„„„„„„1分 (2)40,12 „„„„„„„„„„„„„„„„„„„„„„„„3分 (3)1 „„„„„„„„„„„„„„„„„„„„„„„„„„„4分 (4)甲:y=40x „„„„„„„„„„„„„„„„„„„„„5分 乙:y=28+12 „„„„„„„„„„„„„„„„„„„„„7分 21、解:法一)∵AB=CD,BC=AD
∴四边形ABCD是平行四边形 „„„„„„„„„„„„2分 ∴AB∥CD „„„„„„„„„„„„„„„„„„„„3分 ∴∠BAE=∠DCF „„„„„„„„„„„„„„„„„4分 又∵AE=CF 5分
∴△ABE≌△CDF(SAS) „„„„„„„„„„„„„„ 5分 ∴BE=DF „„„„„„„„„„„„„„„„„„„„6分 法二)如图,连接BF、DE及BD,BD交AC于点D. ∵AB=CD,BC=AD
∴四边形ABCD是平行四边形 „„„„2分 ∴OB=OD,OA=OC „„„„„3分 ∵AE=CF
∴OA-AE=OC-CF 即OE=OF„„„„„„„ 4分
∴△ABE≌△CDF(SAS)„„ 5分
22.设这个一次函数的表达式为y=kx+b „„„„„„ 1分
∵图像过点(1,1)和(-1,-5) „„„„„„ 2分 ∴
解得
„„„„„„ 3分 ∴y=3x-2 „„„„„„„„„„„„„„„„„ 4分 (2)图像与x轴的交点坐标为(
2
3
,0) 图像与y轴的交点坐标为(0,-2) „„„„„„ 5分 S=
12×22
3×2=3
„„„„„„„„„„„„„ 6分 23.(1)依题意得,6x+5y+4(20-x-y)=100 „„„„„„„„„„ 2分
整理得,y=-2x+20 „„„„„„„„„„„„„„„„ 4分 (2) 由得5≤x≤8
因为x取正整数,所以x=5,6,7,8,因此有四种方案 „„„ 6分
(3)设总运费为W,则W=120×6x+160×5y+100×4(20-x-y), 整理得,W=-480x+16000
∵k=-100<0,
∴W随x的增大而减小。 ∴当x=8时,W取得最小值
即选择方案为:装运食品8辆,药品4辆,生活用品8辆,„ 8分
最少费用为:W=-480×8+16000=12160(吨) „„„„„„„ 10分
24. DE=DC„„„„„„„„„„„„„„„„„„„„„„„ 1分
∵∠ABC=450,AD⊥BC
∴△ABD为等腰直角三角形
∴BD=AD„„„„„„„„„„„„„„„„„„„„„„„2分 在RT△BDE和RT△ADC中
BD=AD BE=AC
∴△BDE≌△ADC(HL) „„„„„„„„„„„„„„„„„„5分 ∴DE=DC„„„„„„„„„„„„„„„„„„„„„„„6分
25.解:(1)85.5,80,78,86 „„„„„„„„„„ 4分
(2)从平均数和众数相结合看,八年级的众数较大,八年级的成绩好些
从平均数和中位数相结合看,七年级的中位数较大,七年级的成绩好
些 „„„„„„„„„„„„„„„„„„„„„„„„„„„„„ 6分
(3)如果每个年级选3名,七年级前三名的成绩分别为99,91,89,其平均分为93分;八年级前三名的成绩分别为97,88,88,其平均分为91分;九年级前三名的成绩分别为97,96,89,其平均分为94分,所以九年级的实力更强一些。„„„„„„„„„„„„„„„„„„„„„„„„„„„„„ 8分
5
深圳市龙岗区2015-2016学年八年级(上)期末数学模拟试卷
一、请仔细的选一选(以下每道题只有一个正确的选项,请将答题卡上的正确选项涂黑,每小题3分,共36分) 1. 9的平方根是( )
A.3 B.±3 C.﹣3 2.数
,3.14,
,
,1.732,
,
,
D.±
,﹣O.1010010001…(相邻两个1之间的0的个数逐渐
加1)中,无理数的个数为( )
A.1 B.2 C.3 D.4 3.下面能够成直角三角形三边长的是( ) A.5,6,7
B.5,12,13 C.1,4,9
D.5,11,12
4.下列语句中,是命题的为( )
A.延长线段AB到C B.垂线段最短 C.过点O作直线a∥b D.锐角都相等吗
5.众志成城,抗震救灾.某小组7名同学积极捐出自己的零花钱支援灾区,他们捐款的数额分别是(单位:元):50,20,50,30,50,30,120.这组数据的众数和中位数分别是( ) A.120,50
B.50,20 C.50,30 D.50,50
6.下列各组数值是二元一次方程x﹣3y=4的解的是( ) A.
B.
C.
D.

7.如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )
A.45m B.40m
C.50m D.56m
8.点P(m+1,m+3)在直角坐标系的x轴上,则点P的坐标为( ) A.(0,2) B.(﹣2,0) C.(4,0) D.(0,﹣2) 9.下列函数中,自变量的取值范围选取错误的是( )
A.y=中,x取x≥2 B.y=中,x取x≠﹣1 中,x取x≥﹣3
C.y=2x2中,x取全体实数 D.y=10.下面四个数中与A.2 B.3
最接近的数是( )
C.4 D.5
11.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x+k的图象大致是( )
A. B. C. D.
12.早餐店里,李明妈妈买了5个馒头,3个包子,老板少要1元,只要10元;王红爸爸买了8个馒头,6个包子,老板九折优惠,只要18元.若馒头每个x元,包子每个y元,则所列二元一次方程组正确的是( ) A.
B.
C. D.
二.填空题(每题3分,共12分) 13.
=
14.已知一组数据x1,x2,x3,x4,x5的平均数是3,方差为,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,
3x5﹣2的平均数和方差分别是 , .
15.已知函数y=ax+b和y=kx的图象交于点P(﹣4,﹣2),则二元一次方程组
的解是.
16.在平面直角坐标系中,把直线y=3x沿y轴向下平移后得到直线AB,如果点N(m,n)是直线AB上的一点,且3m﹣n=2,那么直线AB的函数表达式为 . 三.解答题(共52分) 17.(8分)(1)
(2)
﹣
+
.
18.(8分)(1)解方程组:
(2)解方程组:.
19.(5分)如图,飞机在空中水平飞行,某一时刻刚好飞到一男孩子头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米.飞机每小时飞行多少千米?
20.随机抽取某城市一年(以365天计)中的30天的日平均气温状况统计如下:温度(℃)
请根据上述数据回答下列问题: (1)估计该城市年平均气温大约是多少? (2)写出该数据的中位数、众数;
(3)计算该城市一年中约有几天的日平均气温为26℃?
(4)若日平均气温在17℃~23℃为市民“满意温度”,则这组数据中达到市民“满意温度”的有几天?
21.(6分)已知一次函数y=kx+b的图象经过点A(﹣4,0),B(2,6)两点. (1)求一次函数y=kx+b的表达式.
(2)在直角坐标系中,画出这个函数的图象. (3)求这个一次函数与坐标轴围成的三角形面积.
22.(7分)某景点的门票价格规定如表
某校八年(1)(2)两班共102人去游览该景点,其中(1)班不足50人,(2)班多于50人,如果两班都以班为单位分别购票,则一共付款1118元 (1)两班各有多少名学生?
(2)如果你是学校负责人,你将如何购票?你的购票方法可节省多少钱?
23.(10分)如图,点C,B,E在同一条直线上,AC⊥BC,BD⊥DE,AC=BD=6,AB=10,∠A=∠DBE (1)求证:AB∥DE; (2)求CE的长; (3)求△DBC的面积.
本文来源:http://www.guakaob.com/jianzhugongchengkaoshi/643118.html