【www.guakaob.com--励志口号】
如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=42,点D是AC边边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值
GRM9979
一、整体解读
试卷紧扣教材和考试说明,从考生熟悉的基础知识入手,多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力,立足基础,先易后难,难易适中,强调应用,不偏不怪,达到了“考基础、考能力、考素质”的目标。试卷所涉及的知识内容都在考试大纲的范围内,几乎覆盖了高中所学知识的全部重要内容,体现了“重点知识重点考查”的原则。
1.回归教材,注重基础
试卷遵循了考查基础知识为主体的原则,尤其是考试说明中的大部分知识点均有涉及,其中应用题与抗战胜利70周年为背景,把爱国主义教育渗透到试题当中,使学生感受到了数学的育才价值,所有这些题目的设计都回归教材和中学教学实际,操作性强。
2.适当设置题目难度与区分度
选择题第12题和填空题第16题以及解答题的第21题,都是综合性问题,难度较大,学生不仅要有较强的分析问题和解决问题的能力,以及扎实深厚的数学基本功,而且还要掌握必须的数学思想与方法,否则在有限的时间内,很难完成。
3.布局合理,考查全面,着重数学方法和数学思想的考察
在选择题,填空题,解答题和三选一问题中,试卷均对高中数学中的重点内容进行了反复考查。包括函数,三角函数,数列、立体几何、概率统计、解析几何、导数等几大版块问题。这些问题都是以知识为载体,立意于能力,让数学思想方法和数学思维方式贯穿于整个试题的解答过程之中。
1、已知:如图五,在△ABC中,AB=AC,点D是 边BC延长线上一点,点E是边AC上一点,如果0 ∠EBC=∠D,BC=4,cos∠ABC=
(1)求证:
CEAB
13
C
D
.
(
图五)
=
BCBD
;
(2)如果S1、S2分别表示△BCE、△ABD的面积,求:S1S2的值; (3)当∠AEB=∠ACD时,求△ACD的面积.(071上海部分学校)
2、已知:如图六,在矩形ABCD中.AB=3.AD= 4.将一个直角的顶点P放置于对角线AC上,一条直 角边经过点B,另一条直角边与BC和DC的延长线分 别交于点E、Q
(1)如果CE=CQ,求AP的长;
(2)比例式
PEPB
C Q D
(图六)
=
CQBC
是否可能成立?如果可能,求出AP的长,并证明你的结论;
如果不可能,请说明理由.(07。1徐汇区)
3、已知:如图八,在直角坐标平面中,点O为坐标 原点.直线y=
43
x+8分别与x、y轴交于点P、Q,
△ABC的AB边在x轴上,BC⊥x轴,BC与线段PQ 交于点M,AB=BC=6,点P是AB的中点.
(1)求BM的长;
(2)如图九,将△ABC以点P为旋转中心进行旋 转,当△ABC的某一条边同时与x、y轴都有交点(设 与x轴的交点为点E,与y轴的交点为点F)时,△OEF 是否可能会与△OPQ相似?如果△OEF会与△OPQ相 似,那么请求出OE的长;如果△OEF不会与△OPQ 相似,那么请说明理由.(07。1闸北)
(图九)
4、已知:如图一,点D是等腰直角三角形ABC的斜边AB上的一个动点(不与A、B重合),过点D作DE⊥AB交边AC于点F,连结BE.∠E=30°,AB=4. 设DE的长度为x,四边形DBCF的面积为y.
(1)求y与x之间的函数关系式,并指出它的定 义域;
(2)连结BF,①当△BDF与△DBE相似时,求 出x的值;②是否存在x的值,使得△BCF与△DBE 相似?若存在,求出x的值;若不存在,请说明理由.
(071普陀区)
B
(图二)
D
5、已知:如图九,在梯形ABCD中,AD∥BC,AP⊥BC,垂足为点P,AB=CD=2,BC=5,∠B=60°,
(1)求AD的长;
(2)若把三角尺60°的顶点与点P重合,使三角尺绕点P旋转,该60°角的两边PE与PF(看作射线)分别与边AD交于点E(点E不与点A、点D重合),与射线DC交于点F(点F不与点C重合),如设AE为x,CF为y,求y与x的函数关系式,并写出自变量x的取值范围;
(3)在第(2)小题的条件下,三角尺绕点P旋转 过程中,△PED与△PDF这两个三角形中,哪一个三角 形可能成为等腰三角形?如有可能,请指出是哪一个三 角形,并求出AE的长;如不能,请说明理由.
(071青浦)
6.如图十,点A的坐标为(0,5),点B在第一 象限,△AOB为等边三角形,点C在x轴正半轴上. (1)以AC为边,在第一象限作等边△ACE(保 留作图痕迹,不写作法和证明);
(2)设AC与OB的交点为点D,CE与AB的延 长线交于点F,求证:△ADB∽△AFC;
(3)连结BE,试猜想∠ABE的度数,并证明你的猜想;
D
P
C
(图九)
(图十)
(4)若点E的坐标为(s,t),当点C在x正半轴运动时,求s、t的关系式. (071南汇)
7.已知:如图八,△ABC是等边三角形,AB= 4,点D是AC边上一动点(不与点A、C重合),EF 垂直平分BD,分别交AB、BC于点E、F,设CD=x, AE=y.
(1)求∠EDF的度数;
C
D
(
图八)
F
(2)求y关于x的函数解析式,并写出x定义域; (3)过点D作DH⊥AB,垂足为点H,当EH=1时,求线段CD的长.(071卢湾)
8、已知:如图一,在矩形ABCD中,AB=3,BC=3,在BC边上取两点E、F(点E在点F的左边),以EF为边作等边△PEF,使顶点P在AD上,PE、PF分别交AC于点G、H,
(1)求△PEF的边长; (2)求证:
PGGH
P F
C
=
EGGC
D
;
(3)若△PEF的边EF在线段BC上移动.试猜想: E PH与BE有何数量关系?并证明你猜想的结论.(071虹口)
(
图三)
9、如图七,在直角坐标系中有一个半径
为r的圆A,圆心A在x轴的正半轴上,从坐标原点O 向圆A做切线,切点是点B.
(1)如果OB=33,OA与半径r的差是3,求
(图七)
圆A的半径r,点A的坐标及∠AOB的正弦值;
(2)设∠AOB=α,在图中确定一个与2α大小相等的角(可以添加辅助线),并说明理由;
(3)在(2)的基础上,试探究sin2α与2sinα是否相等?如果相等,请说明理由;如果不相等,请你找出它们之间正确的关系式.(071长宁)
10、(本题满分14分,第(1)题3分,第(2)题6分,第(3)题5分) 已知:如图七,在Rt△ABC中,∠C=90°,BC =6,AC=8.点P是边AB的中点,以P为顶点,作 ∠MPN=∠A,∠MPN的两边分别与边AC交于点M、 N.
A
(图七)
M N (1)当△MPN是直角三角形时,求CM的长度;
(2)当∠MPN绕点P转动时,下列式子:(甲)CM·AN,(乙)CN·AM的值是否
保持不变?若保持不变,试求出这个不变的值,并证明你的结论;
(3)连接BM,是否存在这样的点M,使得△BMP与△ANP相似?若存在,请求出这时CM的长;若不存在,请说明理由.(071宝山)
11、如图七,在四边形ABCD中,BD垂直平分 AC,垂足为点O,∠ABD=60°,AB边长为24厘米, ctg∠ADB
=
3
.质点P以4厘米∕秒的速度,从点
D
O A出发沿线路A→B→D作匀速运动,质点Q以5厘米
∕秒的速度,从点D同时出发,沿线路D→C→B→A 作匀速运动.
C (1)求BD和CD的长,并确定四边形ABCD的形状;
(2)求经过多少秒钟,运动中的质点P、Q构成的线段与四边形ABCD的边平行?(不包括起始位置和两点均终止的情况);
(3)如果已知质点P、Q经过12秒后分别到达M、N两点,然后同时沿原路返回,质点P的速度不变,质点Q的速度改变为a厘米∕秒,经过3秒后,P、Q分别到达E、F两点,若△BEF与△AMN相似,求a的值.(061闸北)
(图七)
12、已知:如图八,在△ABC中,AB=AC, ∠BAC =90°,点D、E、F分别在BC、AB、AC边上,BD= DC,BE=AF,EF交AD于点G.
(1)求证:DE=DF;
(2)求证:△DEG∽△DCF;
(3)如果AB=3BE,BE=2
13、抛物线y=
14
A
F
(图八) C
求出所有与△BDE相似的三角形的面积.(051闸北) 2,
x2+
114
x+6与x轴有两个交点A、B(点A在点B的左边),与y
轴交于点C,直线y=kx+b经过点A、C.点D(0,m)(其中m≤6)在y轴上,经过点B、D的直线与直线y=kx+b交于点M,
(1)求k和b的值;
(2)如果以点M、C、D为顶点的三角形与以点M、A、B为顶点的三角形相似,求点D、M的坐标;
(3)在第(2)小题的条件下,求△MCD与△MAB的面积比.(041闸北)
14、在△ABC中,∠BAC=90°,AB=AC=2
2,
A
圆A的半径为1,如图五所示.若点O在BC边上运动 (与点B、C不重合),设BO=x,△AOC的面积为y, (1)求y关于x的函数解析式,并写出函数的定义 域;
(图五) C
(2)以点O为圆心,BO长为半径作圆O,求当圆O与圆A相切时,△AOC的面积.
(2004年上海市中考试题)
15、在△ABC中,∠ABC=90°,AB=4,BC= 3 .点O是边AC上的一个动点,以点O为圆心作半 圆,与边AB相切于点D,交线段OC于点E.作EP ⊥ED,交射线AB于点P,交射线CB于点F.
(1)如图一,求证:△ADE∽△AEP;
(2)设OA=x,AP=y,求y关于x的函数解析 式,并写出它的定义域;
(3)当BF=1时,求线段AP的长.
A
B
P
A O (图一)
(备用图)

16、如图4,直线y=
12
x+2分别交x、y轴于点
A、C,点P是该直线上在第一象限内的一点,PB⊥x 轴,点B为垂足,S△ABP=9 .
(1)求点P的坐标;
(图一)
(2)设点R与点P在同一个反比例函数的图象上,
且点R在直线PB的右侧.作RT⊥x轴,点T为垂足,当△BRT与△AOC相似时,求点R的坐标 .
(2002年上海市中考试题)
17、操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q. 探究:设A、P两点间的距离为x.
(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出函数的定义域;
(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.(图5、图6、图7的形状大小相同,图5供操作、实验用,图6和图7备用)
(2002年上海市中考试题)
18、如图一,在正方形ABCD中,AB=1
,AC是以点B为圆心,AB一段弧,点E是边AD上的任意一点(点E与点A、D不重合),过点E作AC所在圆的切线,交边DC于点F,点G为切点;
(1)当∠DEF=45°时,求证点G为线段EF的中点;
(2)设AE=x ,FG=y,求y关于x的函数解析式,并写出函数的定义域; (3)将△DEF沿直线EF翻折后得△D1EF,如图(2),当EF
56
(图5)
(图6)
(图7)
时,讨论△AD1D
与△ED1F是否相似,如果相似,请加以证明;如果不相似,只要求写出结论,不要求写出理由. (2003年上海市中考试题)
E
F
D1(图一)【在三角形abc中,bc=ac,D是Ab上一点】
C
(图二)
C
(备用图)
C
D
E
F D
D
1、 如图,△ABC中,AB=AC,∠BAC=90°,D是BC边上任意一点,求证BD²+CD²=2AD²
2、 在三角形ABC中,AB=AC=m,P为BC上任意一点,则PA²+PB*PC的值为多少? 解:过点A作AN⊥BC于N。(不妨设P在NC上)
AP^2+PB*PC=AB^2-BN^2+(NC-PC)^2+PB*PC=m^2-BN^2+BN^2+PC^2-2BN*PC+PB*PC=m^2+PC(PC-2BN+PB)=m^2{三角形是等腰三角形}
3、 在三角形ABC中,BC=6,AD是BC边上的中线,交BC于点D,AD=3,AB+AC=8,则三角形ABC的面积是_____
解:
∵AD是中线,BC=6,AD=3
∴∠BAC=90°
∴BA²+AC²=BC²=36
∵AB+AC=8
∴AB²+2AB*AC+AC²=64【在三角形abc中,bc=ac,D是Ab上一点】
∴2AB*AC=64-36=28
AB*AC=14
1/2AB*AC=7
∴△ABC 的面积=7
4、 在三角形ABC中,AB=5,AC=13,高AD=12,则三角形ABC的周长是__42或32___ 5、 在矩形ABCD中,已知AB=3,AD=4,P是AD上的动点,PE垂直于AC于E,PF垂直于BD于F,则PE+PF
等于多少?
解:假设AC、BD的交点是O,连接PO
S△APO=(1/2)AO*PE
S△DPO=(1/2)DO*PF
所以 PE+PF=2S△APO/AO + 2S△DPO/DO
根据勾股定理,AO=DO=5/2
所以 PE+PF=(4/5)*(S△APO+S△DPO)=(4/5)*S△AOD=(4/5)*(3×4÷4)=12/5
6、 E为正方形ABCD的边AB上一点,AE=3 BE=1 P为AC上的动点,则PB+PE的最小值等于多少? 解:两点之间直线最短
在AD上做AF=AP=3
连接FB
这时P点是PB+PE的最小值的点,应该是 根号下(3^2+4^2)=5 7、 如图:已知DE=m,BC=n, ∠EBC与∠DCB互余,求BD²+CE²
解:沿BE和CD做一延长线交点为A.因为∠EBC+∠DCB=90°.所以,∠BAC=90° 所以BD2=AB2+AD2 CE2=AE2+AC2 所以CE2+BD2=AB2+AC2+AE2+AD2 又有∠EAD=∠BAC=90°所以AB2+AC2=BC2=n2 AE2+AD2=ED2=m2
所以有BD2+CE2=m2+n2
8、 已知:△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC=2,求∠BPC的度数。 解:将△CPB绕点C逆时针旋转90度得到△CP'B,连接PP'
所以△CPB全等于△CP'A
所以CP=CP' BP=P'A ∠PCB=∠P'CA
所以∠PCB+
∠ACP=∠P'CA+∠ACP
因为角ACB等于90°所以角P'CP等于90°
在等腰直角三角形P'CP中角CP'P等于45°
因为CP=CP'=2
所以PP'等于2倍根号2
因为AP'=BP=1 AP=3
所以PP'等于根号下AP的平方减AP'的平方
PP'等于2倍根号2

所以角AP'P=90°
所以角CPB=角AP'C=角AP'P+角PP'C=90°+45°=135°
9、 如图,CD是△ABC的中线,CN=MN,求证AM=CB。
10、 (1)如图1,把正方形CGEF的对角线CE放在正方形ABCD的边BC的延长线上(CG>BC),取线段AE的中点M,探究线段MD,MF的关系,并加以证明。
(2)将正方形CGEF绕点C旋转任意角度后(如图3),其他条件不变.【在三角形abc中,bc=ac,D是Ab上一点】
探究:线段ME与MD的关系,并加以说明.
解:(1)线段MD、MF的关系是MD=MF,DM⊥MF。
延长DM交CE于N,连结FD、FN。由正方形ABCD,得AD//BE,AD=DC,所以∠DAM=∠MEN。 因为AM=EM,∠AMD=∠E(……隐藏……)8。因为∠7+∠DCF=∠8+∠FEN=90°,
所以∠DCF=∠FEN,易得△DCF≌△NEF,所以FD=FN,∠DFC=∠NFE。由∠CFE=90°,得∠DFN=90°, 所以MD=MF,DM⊥MF。
11、 矩形ABCD中,AB=20,BC=10。若在AC,AB上各取一点M,N,使BM+MN
的值最小,求这最小值。 解:遇到这类问题我们一般做镜像,也就是做轴对称,作B点关于AC的对称点E,连接AE交CD于F,连接CE,过E作EN垂直AB交CD于G交AC于M,连接MB,所以BM+MN=NM+EM,显然EN垂直AB时值最小.
由于CEF为直角三角形,CF=AF,CF+EF=AE=20;CE=10;所以CE=12.5,EF=7.5,直角三角形EFC斜边高EG=6,所以EN=BC+EG=16.
12、已知正方形ABCD的边长AB=k(k是正整数),正△PAE的顶点P在正方形内,顶点E在边AB上,且AE=1. 将△PAE在正方形内按图1中所示的方式,沿着正方形的边AB、BC、CD、DA、AB、……连续地翻转n次,使顶点第一次回到原来的起始位置. ..P.
(1)如果我们把正方形ABCD的边展开在一直线上,那么这
一翻转过程可以看作是△PAE在直线上作连续的翻转运动. 图2是
k=1时,△PAE沿正方形的边连续翻转过程的展开示意图. 请你探
索:若k=1,则△PAE沿正方形的边连续翻转的次数n= 时,
顶点第一次回到原来的起始位置. ..P.
DCPAEB
图1 B(E)CDABCDABCDABCDAB图2

(2)若k=2,则n= 时,顶点第一次回到原来的起始位置;若k=3,则 ..P.
n时,顶点第一次回到原来的起始位置. ..P.
(3)请你猜测:使顶点第一次回到原来的起始位置的n值与k之间的关系(请用含..P.
k的代数式表示n).
分析:这是一道面动滚动型问题,正△PAE在滚动的过程中,第1次以点E为圆心,第2次以点P为圆心,第3次以点A为圆心第4次又以点E为圆心……,每3次成循环,而半径始终为1。而把四边形展开顶点A、B、C、D、A……,每4个成循环。故问题1转化为求3与4的最小公倍数即12;问题2中,三角形每转2次,顶点才会重合一次,故需24次;问题3中,三角形每转3,顶点A便会与四边形的下一个顶点重合,故仅需12次;总结一、二两题的规律,可归纳得出第3题的结论。
解:(1)12次(2)24次;12次(3)当k是3的倍数时,n=4k;当k不是3的倍数时,n=12k.
12、 设x、y为正实数,且X+Y=4 。 求根号下X的平方加1
加上根号下Y平方加4的最小值?
解:解:令T=√(x^2+1)+√(y^2+4)
则T>0
T^2=x^2+1+y^2+4+2√(x^2+1)(y^2+4)
=x^2+y^2+5+2√(x^2y^2+4x^2+y^2+4)
因为x+y=4 所以(x+y)^2=16 即x^2+y^2=16-2xy
因为x,y都是正实数 所以 4x^2+y^2≥4xy(当且仅当2x=y时取等号)
所以T^2≥21-2xy+2√(x^2y^2+4xy+4)
=21-2xy+2√(xy+2)^2
= 25
因为T>0,所以T≥5(当且仅当2x=y时取等号) 即最小值是5。(此时x=4/3,y=8/3)
13、正△ABC的边长为3厘米边长为1厘米的正
△RPQ的顶点R与点A重合点PQ分别在ACAB上将△RPQ沿着边ABBCCA顺时针连续翻转直至点P第一次回到原来的位置则点P运动路径的长为 解:在AB上翻转时,是两段半径为1,圆心角是120度的弧。
在BC上,CA上也一样。
一共6段,长为3.14*2*1*2=12.56厘米
13、
在菱形ABCD中,AD=BD=6,点E是AD上的一点,AE=2,点P是对角线BD上的一个动点,则PA+PE的最小值。
一、整体解读
试卷紧扣教材和考试说明,从考生熟悉的基础知识入手,多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力,立足基础,先易后难,难易适中,强调应用,不偏不怪,达到了“考基础、考能力、考素质”的目标。试卷所涉及的知识内容都在考试大纲的范围内,几乎覆盖了高中所学知识的全部重要内容,体现了“重点知识重点考查”的原则。
1.回归教材,注重基础
试卷遵循了考查基础知识为主体的原则,尤其是考试说明中的大部分知识点均有涉及,其中应用题与抗战胜利70周年为背景,把爱国主义教育渗透到试题当中,使学生感受到了数学的育才价值,所有这些题目的设计都回归教材和中学教学实际,操作性强。
2.适当设置题目难度与区分度
选择题第12题和填空题第16题以及解答题的第21题,都是综合性问题,难度较大,学生不仅要有较强的分析问题和解决问题的能力,以及扎实深厚的数学基本功,而且还要掌握必须的数学思想与方法,否则在有限的时间内,很难完成。
3.布局合理,考查全面,着重数学方法和数学思想的考察
在选择题,填空题,解答题和三选一问题中,试卷均对高中数学中的重点内容进行了反复考查。包括函数,三角函数,数列、立体几何、概率统计、解析几何、导数等几大版块问题。这些问题都是以知识为载体,立意于能力,让数学思想方法和数学思维方式贯穿于整个试题的解答过程之中。
| 有学生问小编关于下面的这个全等三角形知识点的数学题: 题目如下: 在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE. (1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= _________ 度; (2)设∠BAC=α,∠BCE=β. ①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由; ②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论. |
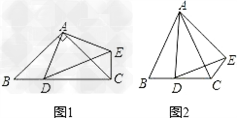 |
| 解:(1)90°. 理由: |
上一篇:升达教务处官网