【www.guakaob.com--三年级】
2014年新教材苏教版
四年级数学上册重要知识盘点
第一单元 升和毫升
1. 1 升(L)=1000毫升(ml 、mL)
2. 从里面量,长、宽、高都是(1分米)的正方体容器的容积正好是( 1 升)。
3. 1 升水重1千克。
4. 一个健康的成年人血液总量约为 4000——5000毫升。义务献血者每次献血量一般为200毫升。
第二单元 两、三位数除以两位数
(1)三位数除以两位数,商可能是( 一 )位数,页可能是( 两 )位数。试商时,一般用(四舍五
入)法将除数看作(整十数)来试商。四舍,除数变小,则初商可能(偏大);五入,除数变大,则初商可能(偏小)。
例:362÷43,将43看作( )来试商,除数变( ),此时初商可能( );
362÷48,将48看作( )来试商,除数变( ),此时初商可能( )。
(2)当被除数的前两位大于或等于除数时,商是(两位数);当被除数的前两位小于除数时,商是(一
位数。)
( )53÷56,若商是一位数,( )里可以填( ),最大是( );
若商是两位数,( )里可以填( ),最小是( );
439÷( )4,若商是一位数,( )里可以填( ),最小是( );
若商是两位数,( )里可以填( ),最大填( )。
(3) 被除数÷除数=商„„余数 验算方法:商×除数+余数=被除数
(4) 商的变化规律:被除数和除数同时乘(或除以)相同的数(0 除外),商不变,但余数却跟着改变。 14÷3 = 4 …… 2 100÷30 =3……10
140÷30 =4 …… 20(余数也扩大10倍) 10÷3 =3 ……1 (余数也缩小10倍)
15÷4=3……3 88÷24=3……16
45÷12=3……9 (余数也扩大3倍) 22÷6=3……4 (余数也缩小4倍)
(5) 同一事物依次重复出现叫做周期现象,发现周期规律至少要观察两组物体的排列。解决周期现象
的问题时,用除法计算比较方便,用总数÷每组个数。如果没有余数,指定的物体就是每组的最后一个;如果有余数,余几就看每组的第几个。
例题:有同样大小的红珠、白珠、黑珠共180个,按3个红珠、2个白珠、1个黑珠的顺序排列着。那
么第96个珠子是( )颜色的,第105个珠子是( )颜色的,红珠有( )个。 第四单元、统计表和条形统计图
1、统计时,数据要按顺序数,遍统计的数据总和是否与题中数据总和相等。
(2)条形统计图:要写好日期,看清每一格代表的数值是多少。 根据数据的多少画出直条的高度, 毎
画好一个柱状图,要在上面写上所对应的数据。
(3)平均数能较好地反映一组数据的(总体情况)。 平均数=总数÷份数,总数=平均数×份数。
第六单元 可能性
公平的游戏规则:所占物体的个数相等,可能性就相等,游戏规则就公平。
第七单元、混合运算:
运算顺序:算式中只有加、减法或者只有乘、除法的,按(从左到右)的顺序依次计算;既有加减法又有乘除法,先算(乘、除法),再算(加、减法);既有小括号,又有中括号,要先算(小括号里面的,再算中括号里的)。括号能改变(计算的顺序。)
典型的简便计算题:
25×17×4 125×32 273-153-47 2700÷15÷2 195×75+195×25
第八单元、垂直与平行线:
1、线段是(有限长)的,有(两个)端点,可以(测量);射线是(无限长)的,只有(一个)端点,不
可以(测量);直线是(无限长)的,(没有)端点,不可以(测量)。
2、经过一点可以画(无数)条直线;经过两点只可以画(一条)直线。
3、同一个平面内可以画(无数)条直线与已知直线垂直,也可以画(无数)条直线与已知直线平行。
过直线外一点可以画( 1 )条直线与已知直线垂直,可以画( 1 )条直线与已知直线平行。
4、连结两点的线段的长度叫做这两点间的(距离)。两点之间,(线段)最短。
直线外一点到这条直线的垂直线段的长度,叫做点到直线的(距离)。从直线外一点到这条直线的所有线段中,(垂直线段)最短。
5、从一点起画两条(射线),可以组成(一个角)。角有(一个)顶点和(两条)边。
6、(量角器)是度量角的工具。把半圆分成180等份,每一份所对的角就是(1度)的角。记作( 1°)。 (“度”)是计量角的单位,用符号(“°”)表示。
7、量角的方法:中心对准顶点,一条边对准0刻度线,看另一条边所对的刻度。(注:角的开口朝哪边,
就看哪边的0刻度线,注意看清是内刻度还是外刻度.)
8、角的大小与(边的长短)无关,与两条边(叉开的大小)有关。两边叉开越大,角就(越大),叉开
越小,角就(越小)。
9、 0°< 锐角 < 90°,直角 = 90°, 90 < 钝角 < 180°,平角 = 180°,周角 = 360° 。
它们的大小排列顺序是:锐角 < 直角
< 平角 < 周角 1周角 = 2平角 = 4直角
10、一副三角尺有两块三角尺,其中一块 含有的角度分别是45°,45°,90°;另一块
含有的角度分别是30°,60°,90°
经过组合,他们可以形成的角有:75°,105°,120°,135°,150°,180°
11、钟面上共有12大格,共360°,每一大格占30°,每一小格占6°。钟面上(3时)和(9时)整,时针和分针组成了(直角);钟面上(6时)整,时针和分针组成了(平角)。
12、三角形三个内角的和=180°,四边形4个内角的和=360°,五边形5个内角的和=540°.
多边形的内角和= (n-2)×180°.
13、三角形最多有(1)个钝角,最多有(1 )个直角;最少有(2 )个锐角,最多有(3)个锐角。
14、两条直线相交成4个角时,对顶角度数相等,相邻的两个角度数和是180°。
如图:2
1 = 3 2 = 4 3 1 + 2 = 180° 2 + 3 = 180°
15、同一平面内相交成直角的两条直线(互相垂直),其中一条直线叫做另一条直线的(垂线),它们的
交点叫做(垂足)。
”。
过一点作已知直线的垂线的方法:一贴、二靠、三移、四画、五标记
16、同一平面内,不相交的两条直线(互相平行),其中一条直线叫做另一条直线的(平行线)。
17、平行线之间的距离(处处)相等。
18、长方形和正方形的对边(互相平行并且长度相等),相邻的两条边(互相垂直)。
19、在物体的质量相同,斜面的长度相同时,物体从(45°)角的斜面上滚下会滚得最远。
20、同一平面内的两条直线,如果不相交,就会(互相平行 )。
例1:判断题。
A、钝角都大于90度。……(√) B、钝角都小于180度。……(√) D、小于180度的角都是钝角。……(×) C、大于90度的角都是钝角。……(×) E、平角就是一条直线。……(×) F、周角就是一条射线。……(×) G、周角只有一条边。……(×) H、永远不相交的两条直线互相平行。……(×) 附:常用的数量关系
正方形的面积=边长×边长
正方形的周长=边长×4 (边长=周长÷4)
长方形的面积=长×宽 (长方形的宽=面积÷长 长方形的长=面积÷宽)
长方形的周长=(长+宽)×2 (长方形的长 = 面积÷2-宽 长方形的宽 = 面积÷2-长) 平均数 = 总数÷份数 (份数=总数÷平均数 总数=平均数×份数)
总价=单价×数量 ( 数量=总价÷单价 单价=总价÷数量) 路程=速度×时间 ( 时间=路程÷速度 速度=路程÷时间)
工作总量=功效×时间 (时间=工作总量÷功效 功效=工作总量÷时间)

2014年苏教版四年级数学上册教案
一、升和毫升
二、两、三位数除以两位数
★简单周期
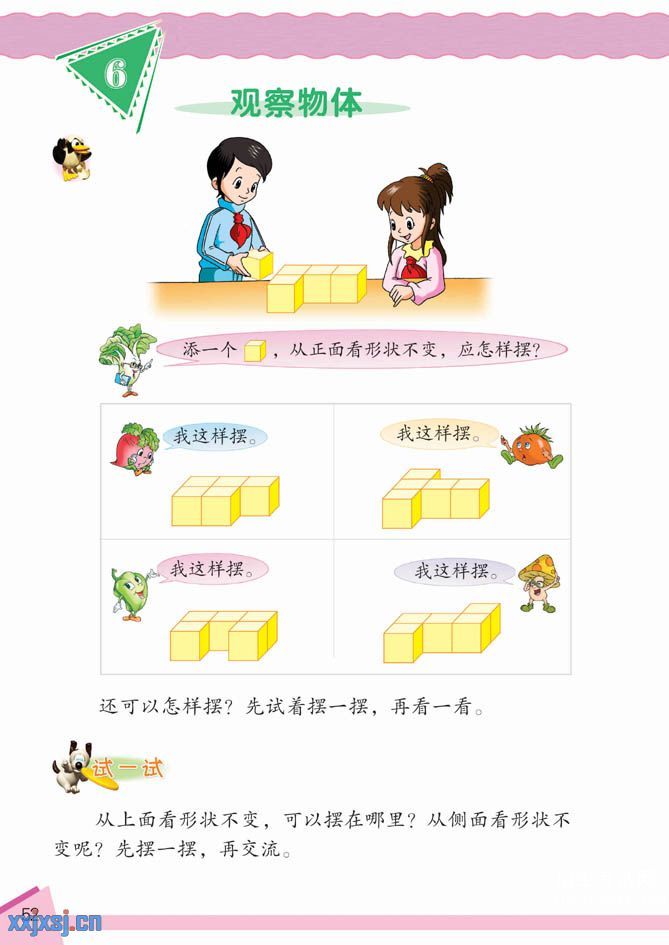
三、观察物体
四、统计表和条形统计图(一)
●运动与身体变化
五、解决问题的策略
六、可能性七、整数四则混合运算
八、垂线与平行线
●怎样滚得远
九、整理与复习
附录 混合运算
2014.9
第一单元:升和毫升
第1课时:认识容量和升
教学内容:教材1-2页例1-例2。
教学目标:
1.使学生在具体情境中感受并认识容量以及容量单位升。
2.使学生初步了解测量、比较容量的方法,能估计一些常见容器的容量,培养估计意识和初步的估计能力。
3.使学生联系实际感受升在日常生活中的应用,能积极参与操作、实验等学习活动,能主动与他人合作交流并获得积极的情感体验。
教学重点:认识容量以及容量单位升。
教学难点:形成一升的具体概念。
学具准备:课件、量杯、纸杯。
教学过程:
一、教学“容量”。
1.老师取两个大小明显有区别的容器,问:这两个容器,哪个可以装得更多?
在学生回答的时候,教学生用“容量”来说一说,指出:这个容器所能装的液体的多少,可称之为“容量”。
2.拿两个差不多大的容器,让学生猜一猜哪个容量比较大,如何验证? 教师根据学生回答进行操作,可以两个容器互相注水比较。
(3)议一议:小红家水壶装满后可以倒5杯,小明家水壶可以装满后可以倒4杯。你认为哪家的水壶更大?为什么?
在学生说理的基础上,得出:要用一个统一的标准来衡量。因为倒的杯子可能有大有小,用它来比是不合适的。
二、认识“1升”
1.出示例2情景图。你们认识这些物品吗?知道物品后面的几升代表什么意思吗?(计量水、油、饮料等液体的多少,通常用“升”做单位。升可以用字母“L”表示。)
2.那么1升有多少呢?我们可以用量杯来量出1升水。师操作用量杯量出1升水,让学生观察。
继续操作:教师取出棱长为1分米的正方体容器,将刚才量出的1升水倒
正方体,让学生观察,你有什么发现?
说一说这个正方体容器的容量是多少?猜一猜正方体的棱长是多少?验证过程中提问:为什么要从里面量?而不从外面量?
3.继续感受1升水多少。
(1)教学“试一试”
先让学生估计下1升水大约能倒满几个纸杯,再验证下(5个)。
(2)再看一看,教室里的这桶纯净水有多少升呢?(19升)这桶水你拎得动么?
介绍:成人一天一般要喝1到1.5升水,孩子要喝1升水,那你知道1升水大约是这样的几杯呢? 想一想,你每天的水喝够了么?
三、练习。
1.练一练第1题。
先让学生观察,同桌交流。指名回答,说明如何比较。
2.练一练第2题。
让学生同桌之间说一说。集体订正。
四、全课总结:
说说今天的学习,让你明白了哪些知识?
教学反思:
第2课时:认识毫升
教学内容:教材第3-4页例3、例4。
教学目标:
1.认识容量单位毫升,知道毫升是一个比较小的容量单位。
2.掌握升和毫升之间的进率,知道1升=1000毫升【2013四年级上册数学课本苏教版】
教学重、难点:认识容量单位毫升,掌握升和毫升之间进率。
教学准备:滴管、量桶、瓶盖、水等。
教学过程:
一、复习导入:
1.上节课我们学习什么?你知道了相关的哪些知识?
取出纸杯,上节课上我们做了实验,1升水大约可以装满几个这样的纸杯(5个)?那么这个纸杯的容量是多少呢?如何精确表示出这个纸杯的容量,就需要一个比较小的容量单位(毫升)。
2.我们日常生活中也可以经常见到毫升这个单位。(出示例3)
师:计量比较少的液体,通常用毫升作单位。毫升可以用字母“ML”表示。
二、认识1毫升
1.取出滴管,介绍:用这个滴管可以量出1毫升的水。现在我们要用这个滴管来找1毫升有多少滴,你有什么好办法?
(先用滴管吸取1毫升,然后慢慢滴出,数一数1毫升的滴数。)
实验:大约是18-20滴。
2.每个组派人上来,用老师准备的滴管在瓶盖内滴20滴水(1毫升),组内传一传,看一看1毫升的水大约是多少?
说一说:1毫升水是多少水呢?
三、教学“1升=1000毫升”
现在我们认识了“毫升”是比较小的容量单位,那么1毫升和1升比较下我们可以发现1毫升的水要比1升水少得多。现在你想不想知道多少毫升水是1升水呢?有什么办法吗?
实验操作,教师取出量杯(500ml)和正方体容器(1L),让学生观察量杯刻度,然后量出量出2杯500ml的水倒入1升的容器,让学生说一说,你有什么发现?
结论:1000毫升=1升 1升=1000毫升
四、完成想想做做:
1.下面的容器里各有多少毫升药水?
指出:饮料我们可以多喝点少喝点,但在医学上却不能有一点点的马虎,所以在用药的时候都要严格按照规定。下面这些是常见的一些规格,分别说说是多少毫升?
2.老师用量筒量出一个50毫升,然后倒入一个常见的一次性透明的杯子里,让学生感受一下其高度,然后再让学生想象如果倒入题中的这几个容器中,水面高度各可能是什么情况?
3.填空:
4升=( )毫升 2000毫升=( )升
9升=( )毫升 5000毫升=( )升
五、全课小结:说说你对毫升的认识。
第3课时:练习一
教学内容:教材第5-7页练习一。
教学目标:
1.通过练习,使学生进一步认识容量单位升和毫升,能正确地使用合适的容量单位。
2.能对一些常见容器的进行估计,提高学生这方面的认识能力。 教学重点:进一步认识容量单位升和毫升,能正确使用合适容量单位。 教学难点:对常见的容器进行估计。
教学过程:
一、复习导入。
1. 关于容量单位你有哪些认识?
2.出示练习一第1题情景图。你发现了什么?
3.练习一第2题。
今天我们继续研究日常生活中的容量单位“升”和“毫升”。
二、练习指导。
1.第3题。
出示各生活用品,先学生估计下容量。再在课本上完成选择。
2.第4题。
学生同桌交流后指名回答。
3.第6题。
出示生活中物品,先让学生估计下容量,再在课本上完成选择。
4.第7题。
学生独立完成,再让学生说一说你是如何选择容器的容量单位的?有什么技巧?
5.第8题。
学生独立完成,集体订正。
6.第9题。
第一单元 升和毫升
第一课时:(认识容量和升)
教材简析:
本课内容包括认识容量以及容量单位升。容量单位经常用来度量容器里容纳液体的体积。本册教材在教学体积之前先教学容量和容量单位,是因为这一内容在日常生活中的应用极为广泛,几乎随时随地都可能接触到。尽量早点教学容量以及容量单位,既方便学生生活,又为以后教学体积积累了感性材料。由于在体积之前教学,因此采取了直观认识、直觉感受为主的教学方法。
第一道例题通过三个活动使学生从不同的层次认识容量这一新的概念,同时产生认识容量单位的心里需求,由此过渡到第二道例题容量单位“升”的教学,感受升在生活中的实际意义,并通过实验认识1升容量的大小,从感性上认识1升有多少。
“想想做做”培养学生以不同的方法比较容器的容量,认识容量单位“升”。
学情分析:
学生的已有生活知识经验是:1.容器越大,能盛的水就越多;2.对正方体容器的感性经验。第一个已有知识经验对学生正确建立“容量”概念的表象至关重要,并为深层次理解“容量”的含义打下基础,学生建立概念的线索是“感性材料→数学含义→概念的具体化”。第二个已有知识经验对学生正确理解、体会“1升到底有多少”也是很重要的;虽然通过一个标有“1L”烧杯似乎也能让学生体会这“1升到底有多少”,但这样无法让学生将“升”的知识与已有知识经验衔接起来,学生的认知也是“无本之木”,是表面化的,很难进行深层次的理解。
教学目标:
1、学生在具体的情境中感受并认识容量,体会计量容量需要有统一的容量单位;联系实际初步形成1升的容量观念,通过实验操作体会1升有多少。
2、学生学会估计一些容器的容量,培养估计意识和初步的估计能力。
3、联系生活实际感受升在日常生活中的应用,能积极参与操作、实验等活动,能主动与他人合作交流,并获得积极的情感体验。
教学重点:认识容量的含义及容量单位升。
教学难点:容量单位1升的观念的建立。
教具、学具准备:电子课件,量杯,每组一把同样大小的水壶,每组不一样大小的杯子,体积是1立方分米的正方体容器,小组自带大小不一的容器。
教学过程
一、创设情境,导入新课
谈话:同学们,动物园里正在举行一场别开生面的争夺冠军比赛,那就是老虎和狮子正在进行的“喝酒决赛”。老虎一连喝了5杯,还没有醉,狮子刚喝了2杯就摇摇晃晃了,老虎得意地说:“我是森林中的酒仙,森林中的冠军!”狮子不服气地嚷道:“你的杯子小,我的杯子大。所以我是冠军!”老虎和狮子谁也不肯让步,争得面红耳赤。
师:同学们,你们认为他们谁说的有道理呢?
生1:老虎一连喝了5杯,还没有醉,狮子刚喝了2杯就撑不住了,所以老虎的肚量大,老虎是冠军。 生2:狮子用的杯子比老虎用的杯子大,所以冠军应该是狮子。
二、探索领悟,认识容量
1、初步认识容量
谈话:同学们的两种想法都有一定的道理,但又不全面,(教师这时取出两个不一样大的杯子。)这是大小不一的两个杯子,这个是老虎用的杯子,而这是狮子用的。
如果有学生说了两种想法,就说:你想得很周到,我们不仅要看喝的杯数,还要看杯子的大小。
提问:同样是一杯酒,你们认为哪一杯多?
生:大的杯子里盛的酒多。 谈话:对,一看就知道大杯子比小杯子盛的酒要多,在数学上,我们就说,盛液体多一些的杯子的容量比较大。盛液体少一些的杯子的容量比较小。
板书:容量
2、加深对容量的认识
出示两个大小不一的杯子1号和杯子2号。
谈话:比较完了狮子和老虎的杯子容量,看看这两个杯子,你觉得哪一个杯子的容量大呢? 生1:杯子1号大。
生2:杯子2号大一些。
谈话:光凭眼睛估计得到的结果可能有误差,我们可以想一个办法来验证说明两个杯子容量的大小。 提问:想个什么办法呢?
生1:我们可以先把杯子1号装满水,倒入杯子2号中,如果杯子2号中水满时,杯子1号中还有水的话,说明杯子1号的容量大,杯子2号的容量小;如果杯子2号里的水没装满,说明杯子2号的容量大。
生2:用同一个杯子往里面倒水,倒得杯数多的那个杯子容器量大。
生3:在这两个杯子里都装满水,把水倒到有刻度的杯子里,数字大的那个杯子的容量大。
谈话:同学们的想法真多啊!根据某某同学说的,我们就用这种倒水来验证一下吧!(根据同学刚才的说法操作验证。)通过这种倒水的方法可以得出水壶一号的容量比较大。
3、做“想想做做”第1题,做“想想做做”第2题。
谈话:比较完了那两个杯子的容量大小,我们现在来比一比这三个杯子的容量大小吧!先猜一猜,这三个杯子的容量关系怎样呢?结果是不是和我们猜测的一样呢?用你喜欢的方法小组一起合作验证一下。
学生操作、交流。
4、进一步感受容量的含义
谈话:现在请同学们观察老师手中这个杯子中盛了多少水。你能说出这个杯子的容量是多少吗?可能一下子回答老师的问题有一点困难,在回答之前我们小组可以讨论一下,或者借助你手边的一些容器,把这一大杯水倒入我们的一次性杯子中,看看可以盛多少杯。
小组活动,将一大杯水分别倒入各自准备的一次性水杯中。
提问:谁来说一说,这一大杯水可以倒几杯?
生1:我们组倒了2杯不到点。
生2:我们小组只倒了3杯半。
生3:我们的小组倒了3杯还多一点。
谈话:如果别人这样告诉你,说这个容器能盛2杯不到,或者说能盛3杯半水,或者说能盛3杯多一点。你能知道这容器的准确容量吗?
谈话:因此,我们需要给容量定出一个统一的标准,这个统一的标准就是我们的容量单位。
三、联系生活,认识容量单位升
1、认识升
谈话:请同学们拿出从家中带来的各种容器,分别在小组里交流一下带来的容器上标明的容量是多少,用的是什么单位。
小组交流。
谈话:生活中有很多的容器上都标有容量单位升或者毫升,亳升这个容量单位,我们下节课再来学习。 提问:你知道图中的这些容器盛的水、油、饮料的容量各是多少吗?一起来看一下。课件出示,学生回答。
明确:计量这些容器盛了多少水、油、饮料等液体,通常用升作单位。升可以用符号“L”来表示。 板书:升、 L
谈话:今天我们这节数学课主要来认识容量和容量单位升。 板书课题:认识容量和升
谈话:老师手中有一个容器,上面标着,“净含量2L”。这里的净含量是什么意思?为什么用净含量而不用容量呢?净含量和容器的容量有什么关系呢?有谁知道吗?
讲述:“净含量”是指某种容器中实际容纳物体的多少。如,一瓶饮料的净含量是1升,是指瓶子里装的饮料本身有1升,但瓶子的容量可能会比1升略大,因为通常不会装的满满的。
2、做“想想做做”第3题。
提问:除了我们课堂上这些容器标有容量大小,生活中我们还会看到另外一些,你见过题目中的3个容器吗?你能分别说出它们的名称和容量吗?
3、认识1升
谈话:我们已经知道计量容量的单位是升,那么1升究竟有多少呢?
谈话:要想科学地认识升这个单位,我们先来认识这个量杯(出示量杯),请组长从袋子中拿出我们的量杯。量杯是用来测量液体容量的工具,在量杯上有一些刻度,标着1的地方就表示容量是1升。 谈话:1升水到底有多少呢,我们来做个实验。(出示正方体)这是一个空心的正方体,它的长、宽、高都是1分米。现在我们在正方体容器内装满水,再将这些水倒入量杯中,看一看有什么发现呢? 生:正方体内的水倒入量杯中正好是1升。
谈话:如果一个容器是正方体,容器内部的长、宽、高都是1分米,这个容器盛的液体正好是1升。 学生回答后教师板书:长、宽、高都是1分米的正方体的容量正好是1升。
4、深化对1升的认识的实践活动。
学生活动一
谈话:看一看我们小组里面有没有容器的容量正好是1升的呢?谁来交流一下。
学生交流。
谈话:虽然这些容器的形状不一样,但是它们的容量都是1升。
学生活动二(想想做做第一题)
谈话: 下面这些容器你见过吗?我们一起来看一下。
出示课件。下面哪些容器的容量比1升大?
(设计意图:加强学生的估算意识和学习估算容量的方法)
学生活动三
谈话:看,老师给你们准备一些容器,你能根据刚才我们对1升的认识,估计一下它的容量吗? 学生估计。
谈话:刚才我们学生估计地对不对呢?我们来验证一下吧!
学生实验验证。
交流反馈。
谈话:通过我们实验,我们得出了热水瓶的容量是?脸盆呢?沙锅呢?我们这个碗呢?还有我们这个烧水壶呢?
机动:看来通过刚才的实验,我们对一些容器有了一定的估计能力。
第14页
四、总结评价,课外延伸
1、同学们,通过这节课的学习,你学得愉快吗?谁能说说你的收获是什么?你还想了解什么?
2、如果老虎和狮子要举行第二次比赛,你认为应该有一些什么规定?
板书设计:
认识容量和升
容量 升 L
长、宽、高都是1分米的正方体的容量正好是1升。
教学反思:
第二课时
教学目标:
1、 让学生在自制量器的过程中感受并进一步认识容量以及容量单位升。
2、 让学生练习估计一些常见的容器的容量,并能对自己的估计作适当解释,培养学生的估计意识和初
步的估计能力。
3、 让学生练习用自制的量器测量一些液体的多少,并能运用所学知识对现实情境中提取的数学问题加
以解释和说明。
4、 培养学生探求新知的兴趣,培养主动与他人合作交流的意识,并在探索中体验成功的喜悦。 教学重点和难点:重点:感知1升有多少。难点:培养学生对容量的估计能力。
教学准备:多媒体课件
教学过程:
一、 复习引入
提问:请同学们回忆上节课我们学习了哪些知识?(了解了容量的含义、认识了升;还知道长、宽、高都是1分米的正方体容器的容量是1升)
升可以用什么字母符号来表示?(L)
这节课我们继续研究升。(板书课题:认识升)【2013四年级上册数学课本苏教版】
二、 自主探究,实践求知
1. 谈话:同学们想不想自己动手制作一个1升的量器?(学生会兴趣高涨,急于表现自己)
2. 出示题目要求:做一个1升的容器,并分别标出1/4升、1/2升和3/4升。
(1) 让学生根据手中的材料,以组为单位讨论怎样做。
(2) 每组选一人汇报讨论方案。
(3) 选出可行的方案(往一个上下一样粗的瓶子里倒入1升水,在瓶上贴上纸条,在1升处记上记
号。把纸条1升处以下的部分平均分成4份,并分别做上记号)。
(4) 动手制作。
教师加强巡视,注意个别指导。
3.提问
(1)哪个小组愿意汇报你们是怎样制作的?
(2)有没有不同的标法?(1/2L和2/4L)它们的大小相同吗?(一样大)
4.用自己做的1升的量器来量一量
(1)量出1升水,试一试1升水能倒满几纸杯?
让学生在组内合作完成。待学生做完后,提问:
1升水能倒满几纸杯?
你一天能喝这样的几纸杯水?你喝的水够1升吗?
谈话:同学们要注意每天多喝水,预防疾病的发生。
(2)先估计桌子上放着的一碗水比1升多还是比一升少,再量一量它大约有多少升。
先让学生以前获得的感受与经验把一碗水与1升水进行比较,让学生充分发表自己的估计意见。
再实际量一量,来验证估计。
三、 运用新知,展示能力
1. 做“想想做做”第1题
(1) 让学生拿出带来的容器,例如碗、锅、盆等。
(2) 用自制量器盛1升水。
(3) 把水倒入自带容器里,观察水面高度。
(4) 观察本组其他同学容器里水的高度。
(5) 全组同学一起讨论,估计这些容器的容量各是多少升,再量一量。看哪组估计的水平高。
2. 解决白菜博士提出的问题
(1) 谈话:再找几个容器,先估一估能盛多少升水,再用自制量器量一量。
(2) 学生估计并动手量。
(3) 汇报估计和测量的结果。
四、 解决问题,升华提高
1. 做“想想做做”第2题
谈话:下面检验同学们的眼力怎样。
让学生读书上的题目。
指名说说容器的名称。
各自作出判断,做在书上。
指名说答案,全班共同校对。
2. 做“想想做做”第3题
谈话:知道了1升水有多少,那么想不想知道1升水有多重?想一想,怎样称出1升水的重量? 学生分组活动。各组汇报称法和结果。
根据学生汇报板书:1升水正好是1千克。
五、 总结评价,拓展延伸
谈话:这节课同学们能积极动脑筋,与同伴合作一定收获不小吧。谁能谈谈有什么收获? 关于容量的知识还有很多,下节课我们将进一步学习。
教学反思:
第三课时:(认识毫升)
教学目标:
1.使学生在具体的观察、操作中感受毫升,联系实际初步形成1毫升的容量观念。
2.掌握升和毫升的进率,能进行简单的换算。
3.能估计一些常见容器的容量,培养估计意识和初步的估计能力。
4.使学生联系实际感受毫升在日常生活里的应用,能积极参与操作、实验等学习活动,能主动与他人合作交流并获得积极的情感体验。
教学重点、难点:正确感知毫升以及升和毫升的关系。
教学准备:多媒体课件、滴管、水、量杯、饮料等
四年级数学上册知识点总结
一、除法:
(1)试商时,将除数看作最接近的整十数来试商,若除数变大,则初商可能偏小;若除数变小,则初商可能偏大。
例1:362÷43,将43看作(40)来试商,此时初商可能(偏大);
362÷48,将48看作(50)来试商,此时初商可能(偏小)。
(2)()53÷56,若商是一位数,()里可以填(5,4,3,2,1),最大是(5); 若商是两位数,()里可以填(6,7,8,9),最小是(6)。 439÷()4,若商是一位数,()里可以填(4,5,6,7,8,9),最小是(4); 若商是两位数,()里可以填(3,2,1),最大填(3)。 (3)被除数÷除数=商„„余数 则 被除数=商×除数+余数
除数=(被除数-余数)÷商 商=(被除数-余数)÷除数
例2:一个数是786,除以24得到余数是18,求商是多少?
解:(786-18)÷24
=786÷24 =32
(4)被除数和除数同时扩大或缩小相同的倍数,商不变,若有余数,余数同时扩大或缩小相同的倍数。
14÷3=4……2(同时扩大10倍) 100÷30=3……10(同时缩小10倍)
140÷30……20
10÷3=3……1
15÷4=3……3(同时扩大3倍) 88÷24=3……16(同时缩小4倍)
45÷12=3……9 22÷6=3……4
二、角:
1、射线、直线、线段定义及特征:,
射线:把线段的一端无限延长,就得到一条射线。 直线:把线段的两端无限延长,就得到一条直线。
线段:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。
射线、直线、线段特征:
经过一点可以画无数条直线,经过两点只可以画一条直线。两点之间线段最短。两点之间线段的长度叫做这两点的距离。
2、角的定义:从一点引出两条射线,所组成的图形叫做角。
角的各部分名称:这一点是角的顶点。两条射线是角的边,可无限延长,但角大小不变。角通常用符号∠来表示。角的大小与两边叉开的大小有关。 3、角的度量:用量角器测量角的大小要求“三个重合,一个注意” A/点点重合:中心点与顶点重合。 B/线边重合:0刻度线与角的一边重合。
C/线边重合:刻度线与角的另一边重合,即读出几度。
注意:量角器内圈刻度与外圈刻度不能混合使用。 5、 角的分类:

锐角:小于90° 直角:等于90° 钝角:大于90°,小于180°
平角:等于180°,一条射线绕着它的端点旋转到恰好成一条直线时,形成的角。 周角:等于360°,一条射线绕着它的端点旋转一周,所形成的角。
例1:判断题。
A、钝角都大于90度。……(√)
B、钝角都小于180度。……(√)
C、小于180度的角都是钝角。……(×D、大于90度的角都是钝角。……(×)
E、平角就是一条直线。……(×) G、周角只有一条边。……F、周角就是一条射线。……(×)
( 含有的角度分别是45°,45°,90°
30°,60°,90°
15°,75°,105°,120°,135°,150°,
180°
(5)钟面上共有12大格,共360°,每一大格30°,每一小格6°。
例2: 3点和9点,分、时针形成的角是(直角)。
6点,分、时针形成的角是(平角)。 6:30是(锐角)
3:30是(锐角、75°)
9:30是(钝角、105°)
4:00是(钝角、120°)
三、混合运算:
运算顺序:有括号要先算括号,然后先算乘除法,后算加减法。
只有加减法或乘除法的时候,要(从左到右,依次计算)。
1、乘法与加减法的混合运算:计算不含括号的混合运算算式时,要先算乘
法后算加减法。
2、除法与加减法的混合运算:计算不含括号的混合运算算式时,要先算除
法后算加减法。
3、含有小括号的混合运算:在含有小括号的混合运算中,不管算式中有加、
减、乘、除哪种运算,都要先算括号内的,再算括号外的。
四、平行与相交
1.线的平行线。
同一平面内,一条直线的平行线有无数条。
同一平面内,两条直线的位置关系只有两种:相交或平行。不相交就一定平行。
例:始终不相交的两条直线互相平行。……(×)
2.垂直:两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一
条直线的垂线,这两条直线的交点叫做垂足。
3.从直线外一点到这条直线所画的,叫做这点到这条直线的离。
从直线外一点到这条直线所画的线段中,垂直线段最短。
五、找规律
(1)在马路一侧种树,1.若两头都种:树的棵树-1=段数
2.若其中一头种,另一头不种:段数=树的棵树 3.若两头都不种:树的棵树+1=段数
(2)若是一个闭合的图形,如:池塘一周、长方形或是三角形一周等,树的棵树=段数。
六、运算律
1.a+b=b+a
a×b=b×a
结合律:(a+b)+c=a+(b+c) 结合律:(a×b) ×c=a×(b×c) 例:37+56+63=56+(37+63) 运用了(加法交换律和结合律)
25×13×4=13×(25×4) 运用了(乘法交换律和结合律) 例2:简便运算:327-(127+100)=327-127-100……减法的性质 720÷54=720÷(6×9)=720÷9÷6……
125×25×32=(125×8)×(25×4)
七、解决问题的策略
1、用列表的方法整理相关信息,弄清题中的数量关系,找出解题的思路,解决“归一”问题。
2、用列表的方法整理相关信息,弄清题中的数量关系,找出解题的思路,解决“求两积之和”的实际问题。
八、统计与可能性
(1)统计时,数数据要按顺序数,不能重复,也不能遗漏,每数一个都要做好标记。
统计完之后,检查一遍统计的数据总和是否与题中数据总和相等。
(2)画柱状图时:要写好日期,看清每一格代表的数值是多少。每画好一个柱状图,要在上面或旁边写上所对应的数据。
九、认数
1、计数单位:如个、十、百、千、万„„。相邻两个计数单位之间的进率是10
的计数单位,叫十进制计数法。
2、数位:如个位、十位、百位、千位、万位„„
① 从高位起,一级一级地往下读;
② 亿级、万级的数按个级的读法来读,后面加“亿(万)”字; ③ 每级中间的一个或连续几个0,只读一个0。末尾的0都不读。 5、数的写法:
上一篇:高三政治教后不足
下一篇:2016三年级下册的应应题