七年级下册数学习题三角形内角和180度专练

【www.guakaob.com--一年级】

七年级下册数学习题三角形内角和180度专练(一)
七年级数学三角形的内角和专题练习

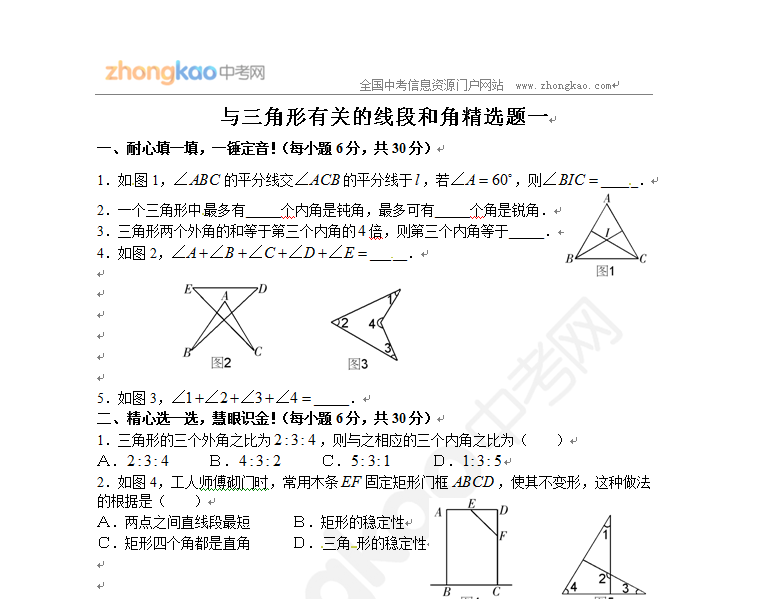
七年级下学期周周练( 7．5三角形的内角和)

(60分钟，满分100分)

一、填空题(6题，每题3分，共18分)

1．△ABC中，∠A=40o，∠B=60o，则与∠C相邻外角的度数是______．

2．三角形三个内角的比为2：3：4，则最大的内角是_______度．

3．如果△ABC扣，∠A+∠B=∠C—10o，则△ABC是________三角形．

4．一个五边形的4个内角都是100o，则第五个内角的度数是_______．

5．一个n边形的内角和与外角和的比为2：1，则n=________．

6．三角形三个外角的比为2：3：4，则三个内角的比为_______．

二、选择题(6题，每题3分，共18分)

7．一个多边形的每个内角都等于156o，则此多边形是 ( )

A．十五边形 B．十六边形 C．十七边形 D．十八边形

8．具备下列条件的△ABC中，不是直角三角形的是 ( )

A．∠A+∠B=∠C B．∠A—∠B=∠C

C．∠A：∠B：∠C=1：2：3 D．∠A=∠B=3∠ 9．一个三角形的三个外角中，钝角的个数最少为 ( )

A．0个 B．1个 C．2个 D3个

10R占去的绿化园地的面积为 ( )

A．2 7R2 B．47R2 C2

11(即图中标有1、2、3、4的四

块)?应该带

( )

1 B．第2块 C．第3块 D．第4块

a照射到平面镜CD上，然后在平面镜舳和CD之间来回反射，这时光

l=∠6，∠5=∠3，∠2=∠4．若已知∠l=55o，∠3=75o，那么∠2等于 ( )

A．50o B．55 o C．66 o D 65 o

三、解答题(8题，共64分)

13．(本题6分)如图所示，求∠A+∠B+∠C+∠D+∠E+∠F的度数．

14．(本题6分)已知：在△ABC中，∠A+∠B=2∠C，∠A—∠B=20o，求三角形三

个内角的度数．

15．(本题8分)如图，∠A=65o，∠ABD=30o，∠ACB=72o，且CE平分∠ACB，求

∠BEC的度数．

16．(本题8分)如果一个n2：3，

求这个多边形的内角和．

17．本题8分)90o，求

这个多边形的内角和．

18．(本题8分)B、∠C的平分线交于点O．

(1)若∠

(2)设∠)，求∠BOC的度数．

(3)ABOC=3∠

A?

19．(本题10分)一个同学在进行多边形的内角和计算时，所得的内角和为1125o，当发

现错了以后，重新检测发现少了一个内角，问这个内角是多少度，他所求的是几边形的内角和?

20．(本题10分)连接多边形不相邻的两个顶点的线段，叫做多边形的对角线，如图(1)，

AC、AD是五边形ABCDE的对角线．思考下列问题：

(1)如图(2)n边形A1，A2，A3…An中，过顶点A1可以画______条对角线，它们分别

是________；过顶点A2可以画________条对角线，过顶点A3可以画条对角线．

(2)过顶点A1的对角线与过顶点A2的对角线有相同的吗?A3的对角线有相同的吗?

(3)

参考答案

1．o 2．80o

3．钝角

4．140o

5．6

6．5：3：1

二、选择题

7．A 8．D 9．C

10．C 11．B 12．D

三、解答题

13．360o

14．∠A=70o、∠B=50 o、∠C=60 o

15．∠BEC=131o 16．540o

17．1080o

18．(1) ∠BOC=115o

(2) ∠BOC=90o+1on 2

(3) ∠A=36o

19．135o 九边形

20．(1)n-3

A1A3、AlA4、A1A5、…、A1An-1

(2)没有对角线相同 有一条对角线相同(即A1A3),

七年级下册数学习题三角形内角和180度专练(二)
北师大版七年级数学下册《三角形的内角和》练习题

七年级下学期三角形的内角和练习题

(60分钟，满分100分)

一、填空题(6题，每题3分，共18分)

1．△ABC中，∠A=40o，∠B=60o，则与∠C相邻外角的度数是______．

2．三角形三个内角的比为2：3：4，则最大的内角是_______度．

3．如果△ABC扣，∠A+∠B=∠C—10o，则△ABC是________三角形．

4．一个五边形的4个内角都是100o，则第五个内角的度数是_______．

5．一个n边形的内角和与外角和的比为2：1，则n=________．

6．三角形三个外角的比为2：3：4，则三个内角的比为_______．

二、选择题(6题，每题3分，共18分)

7．一个多边形的每个内角都等于156o，则此多边形是 ( )

A．十五边形 B．十六边形 C．十七边形 D．十八边形

8．具备下列条件的△ABC中，不是直角三角形的是 ( )

A．∠A+∠B=∠C B．∠A—∠B=∠C

C．∠A：∠B：∠C=1：2：3 D．∠A=∠B=3∠C

9．一个三角形的三个外角中，钝角的个数最少为 ( )

A．0个 B．1个 C．2个 D．3个

10．如图，一块四边形绿化园地，四角都做有半径为R的圆形喷水池，则这四个喷水池

占去的绿化园地的面积为 ( )

A．2 7R2 B．47R2 C．R2 D．不能确定

11．小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四 块)，你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形?应该带

( )

A．第1块 B．第2块 C．第3块 D．第4块

12．如图，光线a照射到平面镜CD上，然后在平面镜舳和CD之间来回反射，这时光

线的入射角等于反射角，即∠l=∠6，∠5=∠3，∠2=∠4．若已知∠l=55o，∠3=75o，那么∠2等于 ( )

A．50o B．55 o C．66 o D 65 o

三、解答题(8题，共64分)【七年级下册数学习题三角形内角和180度专练】

13．(本题6分)如图所示，求∠A+∠B+∠C+∠D+∠E+∠F的度数．

14．(本题6分)已知：在△ABC中，∠A+∠B=2∠C，∠A—∠B=20o，求三角形三

个内角的度数．

15．(本题8分)如图，∠A=65o，∠ABD=30o，∠ACB=72o，且CE平分∠ACB，求

∠BEC的度数．

16．(本题8分)如果一个n边形的内角都相等，且它的每一个外角与内角的比为2：3，

求这个多边形的内角和．【七年级下册数学习题三角形内角和180度专练】

17．本题8分)如果一个多边形的每个内角都相等，每个内角与每个外角的差是90o，求

这个多边形的内角和．

18．(本题8分)如图，在∆ABC中，∠B、∠C的平分线交于点O．

(1)若∠A=50o，求∠BOC的度数．

(2)设∠A=no(n为已知数)，求∠BOC的度数．

(3)当∠A为多少度时，∠BOC=3∠A?

19．(本题10分)一个同学在进行多边形的内角和计算时，所得的内角和为1125o，当发现错了以后，重新检测发现少了一个内角，问这个内角是多少度，他所求的是几边形的内角和?

20．(本题10分)连接多边形不相邻的两个顶点的线段，叫做多边形的对角线，如图(1)，

AC、AD是五边形ABCDE的对角线．思考下列问题：

(1)如图(2)n边形A1，A2，A3…An中，过顶点A1可以画______条对角线，它们分别

是________；过顶点A2可以画________条对角线，过顶点A3可以画条对角线．

(2)过顶点A1的对角线与过顶点A2的对角线有相同的吗?过顶点A1的对角线与过顶点A3的对角线有相同的吗?

(3)在此基础上，你能发现竹边形的对角线条数的规律吗?

参考答案

一、填空题

1．100o

2．80o

3．钝角

4．140o

5．6

6．5：3：1

二、选择题

7．A 8．D 9．C 10．C 11．B 12．D

三、解答题

13．360o

14．∠A=70o、∠B=50 o、∠C=60 o

15．∠BEC=131o

16．540o

17．1080o

18．(1) ∠BOC=115o

(2) ∠BOC=90o+1on 2

(3) ∠A=36o 19．135o 九边形

20．(1)n-3 A1A3、AlA4、A1A5、…、A1An-1

(2)没有对角线相同

(3)n(n3)

2

有一条对角线相同(即A1A3),

七年级下册数学习题三角形内角和180度专练(三)
初一数学人教版(下册)与三角形有关的角练习题一(含答案)

与三角形有关的角课时练

第一课时7.2.1与三角形有关的内角

1.在我们的生活中处处有数学的身影，请看图，折叠一张三角形纸片，

把三角形的三个角拼在一起，就得到一个著名的几何定理，请你写

出这一定理的结论：三角形的三个内角和等于 °

2.在△ABC中，若∠A=∠B=1

2∠C，则∠C等于（ ）

A.45° B.60° C.90° D.120°

3.一个三角形的内角中，至少有（ ）

A一个内角 B.两个内角 C.一内钝角 D.一个直角

4.如图所示，∠1+∠2+∠3+∠4的度数为（ ）

A100° B.180° C.360° D.无法确定

5.如图所示，AB∥CD，AD，BC交于O，∠A=35°，∠BOD=76°，则∠C的度数是（ ）

A.31° B.35° C.41° D.76°

6.在△ABC中：（1）若∠A=80°，∠B=60°，则∠

（2）若∠A=50°，∠B=∠C，则∠C=

（3）若∠A∶∠B∶∠C=1∶2∶3，则∠A= ∠B= ∠C= ；

（4）若∠A=80°，∠B-∠C=40°，则∠C=

7.如图所示，∠1+∠2+∠3+∠4的度数为

8.一幅三角板，如图所示叠放在一起，则 2中a的度数为（ ）

A.75° B.60° C.65° D.55°

9.如图所示，AD、AE分别是△ABC的角平分线和高，若∠B=50°，∠C=70°， 求∠DAC的度数.

第一课时答案：

1.180；2.C，提示：依据三角形内角和定理得，1

2∠C+12∠C+∠C=180°，解得∠C=90°；

3.B；4.C，提示：作如图辅助线，这样把∠1、∠2、∠3、∠4

四个角的和转化为两个三角形的内角和，

即2×180°=360°

5.C，提示：∵AB∥CD，∴∠D=∠A=35°. ∠DOC=180°-∠BOD=180°-76°=104°， 在△COD中，∠C=180°-∠D-∠DOC=180°-35°-104°=41°；

6.（1）40°；（2）65°；（3）30°，60°，90°（4）30°

7.300°，提示：∵∠1+∠2=180°-30°=150°，∠3+∠4=180°-30°=150°，

∴∠1+∠2+∠3+∠4=150°+150°=300°；8.A

9.解：∵∠B=50°，∠C=70°，

∴∠BAC=60°，又∵AD是△ABC的角平分线

∴∠BAD=1

2BAC30.又∵AE是△ABC的高 

∴∠BAE=180°-∠B-∠AEB=40°，∴∠DAC=∠BAE-∠BAD=10°.

第二课时7.2.2三角形的外角

1.根据图形填空：

（1）如图①，已知∠A=72°，∠B=38°，则∠ACD= .；

（2）如图②已知AC⊥BC∠CBD=148°，则∠A= ；

（3）如图③，x= ；

（4）如图④∠A =∠B=∠C=x，则∠；

2.如图所示，已知AB∥CD，∠A=55°，∠C=20°，则∠；

3.如图所示，∠A +∠B+∠C+∠D+∠；

4.如图所示，已知AB∥CD，则（ ）

A. ∠1=∠2+∠3 .B.∠1=2∠2+∠3 C. ∠1=2∠2-∠3 D. ∠1=180°-∠2-∠3 5如图所示，D是△ABC边AC上的一点，E是BD上的一点，∠1，∠2，∠A之间的关系描述正确的是（ ）

A. ∠A ＜∠1＞∠2 B. ∠2＞∠1＞∠A C. ∠1＞∠2＞∠A D.无法确定

6..若一噶三角形三个内角的度数之比为1∶2∶3，则与之相邻的三个外角的度数之比为（ ）

A. 1∶2∶3 B. 3∶2∶1 C. 3∶4∶5 D. 5∶4∶

3

7.一个零件的形状如图所示，按规定∠A应等于90°，∠B和∠C应分别是32°和21°，检验工人量得∠BDC=148°，就断定这个零件不合格，运用三角形的有关知识说明零件不合格的理由.

8如图所示，在△ABC中，∠A=60°，BD，CE分别是AC，AB 上的高，H是BD，CE的交点，求∠BHC的度数.

第二课时答案：

1.（1）110°（2）58°（3）60°（4）120°；2.35°；3.180°，提示：因为∠1=∠B+∠D，∠2=∠C+∠E，所以∠A +∠B+∠C+∠D+∠E=∠A+∠1+∠2=180°；4.A，提示：因为AB∥CD，所以∠ABD=∠3，因此∠1=∠2+∠ABD=∠2+∠3；5.B，提示：三角形的一个外角大于与它不相邻的任何一个内角，故选B；6.D，提示：设三角形三个内角分别为x,2x,3x，则x2x3x180，解得x30，所以三角形三个内角分别为30°，60°，90°，与之相邻的三个外角的度数分别为150°，120°，90°，所以选D；

7.解：如图，连接AD并延长至E，

则∠CDE=∠C+∠CAD，∠BDE=∠B+∠BAD，

所以∠BDC=∠CDE+∠BDE

=∠C+∠CAD+∠B+∠BAD=21°+32°+90°=143°≠148°，

所以这个零件不合格.

8.解：因为BD，CE分别是AC，AB 上的高，所以∠ADB=∠BEH=90°，

所以∠ABD=180°-∠ADB-∠A=180°-90°-60°=30°， 因此∠BHC=∠BEH+∠ABD=90°+30°=120°.



七年级下册数学习题三角形内角和180度专练(四)
苏科版数学七年级下册第7章第8课时《三角形的内角和》课时练习含答案

第8课时 三角形的内角和(1)

1．下面四个图形中，能判断∠1>∠2的是 （ ）

2．关于三角形内角的叙述错误的是 ( )

A．三角形三个内角的和是180º B．三角形两个内角的和一定大于60º

C．三角形中至少有一个角不小于60º D．三角形中最大的角所对的边最长

3．三角形的一个外角小于和它相邻的内角，则此三角形是 ( )

A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定

4．(1)（2010．德州）如图①，直线AB∥CD，∠A＝70º，∠C＝40º，则∠E＝______．

(2)（2010．镇江）如图②，在Rt△ABC中，∠ACB＝90º，DE过点C，且DE∥AB，

若∠ACD＝50º，则∠A＝______，∠B＝______．

(3)（2010．滨州）如图③，AB∥CD，BE平分∠ABC，且交CD于D点，∠CDE＝

150º，则∠C＝______．

5．(1)在△ABC中，若∠A＝100º，∠B－∠C＝20º，则∠B＝______，∠C＝______．

(2)在△ABC中，若∠A：∠B：∠C＝5：1：3，则∠B＝______，∠C＝______．这是

______三角形．

(3)在△ABC中，∠A＝11∠B＝∠C．则∠A＝______，∠B＝______．这是______23

三角形．

(4)若△ABC的三个内角的度数之比为3:4:5．则相应外角的度数之比为______．

(5)等腰三角形的一个内角为40º，则另外两个内角为____________．

6．如图，∠A＝65º，∠ABD＝30º，∠ACB＝72º，且CE平分∠ACB，求∠BEC的度数．

7．如图，将三角尺的直角顶点放在直尺的一边上，∠l＝30º，∠2＝50º，则∠3的度数是

( )

A．50º B．30º C．20º D．15º

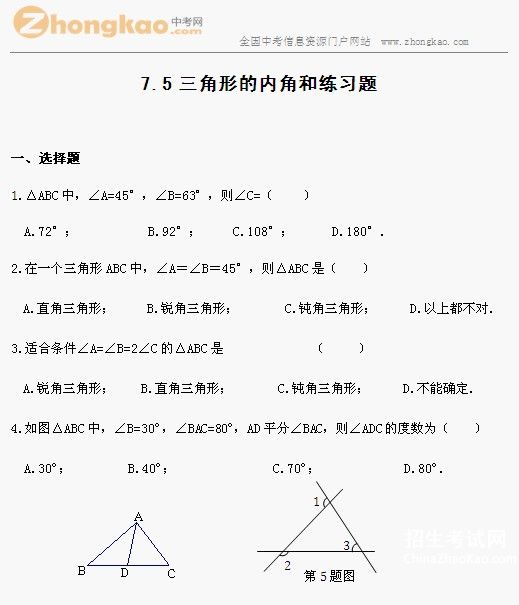
8．如图，AB∥CD，∠A＝50º，∠C＝∠E，则∠C的度数是 ( )

A．20º B．25º C．30º D．40º

9．如图是一张直角三角形纸片，剪去直角后，得到了一个四边形，则∠1＋∠2＝______º．

10．如图，一副三角板叠放在一起，则图中∠1＝______º．

11．如图，D是△ABC的BC边延长线上的一点，DF⊥AB于点F，∠A＝48º，∠D＝

36º，则∠ACB＝______º．

12．如图，在△ABC中，∠ABC与∠ACB的平分线交于点O，若∠A＝50º，则∠BOC＝

______º．

13．如图，求∠A＋∠B＋∠C＋∠D＋∠E的值．

14．生活中我们经常会看见类似下面图形的物体，如：指路牌、飞梭等，在这个图形中，四个角之间存在一个数量关系，即∠BDC＝∠A＋∠B＋∠C．你能说明其中的理由吗？

参考答案

1．D 2．B 3．C 4．(1) 30' (2) 500 400 (3) 1200【七年级下册数学习题三角形内角和180度专练】

5． (1) 50º 30º (2) 20º 60º 钝角 (3) 30º 60º 直角 (4)9：8：7

(5)40º、100º或70º、70º 6． 131º

7．C 8．B 9．270 10． 75 11．78 12．115 13．180º

14．点拨：连接并延长AD．根据三角形内、外角的关系说明．

七年级下册数学习题三角形内角和180度专练(五)
2016最新北师大版七年级数学下册《三角形的内角和》练习题

七年级下学期三角形的内角和练习题

(60分钟，满分100分)

一、填空题(6题，每题3分，共18分)

1．△ABC中，∠A=40o，∠B=60o，则与∠C相邻外角的度数是______．

2．三角形三个内角的比为2：3：4，则最大的内角是_______度．

3．如果△ABC扣，∠A+∠B=∠C—10o，则△ABC是________三角形．

4．一个五边形的4个内角都是100o，则第五个内角的度数是_______．

5．一个n边形的内角和与外角和的比为2：1，则n=________．

6．三角形三个外角的比为2：3：4，则三个内角的比为_______．

二、选择题(6题，每题3分，共18分)

7．一个多边形的每个内角都等于156o，则此多边形是 ( )

A．十五边形 B．十六边形 C．十七边形 D．十八边形

8．具备下列条件的△ABC中，不是直角三角形的是 ( )

A．∠A+∠B=∠C B．∠A—∠B=∠C

C．∠A：∠B：∠C=1：2：3 D．∠A=∠B=3∠C

9．一个三角形的三个外角中，钝角的个数最少为 ( )

A．0个 B．1个 C．2个 D．3个

10．如图，一块四边形绿化园地，四角都做有半径为R的圆形喷水池，则这四个喷水池

占去的绿化园地的面积为 ( )

A．2 7R2 B．47R2 C．R2 D．不能确定

11．小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四 块)，你认为将其中的哪一块带去，就能配一块与原来一样大小的三角形?应该带

( )

A．第1块 B．第2块 C．第3块 D．第4块

12．如图，光线a照射到平面镜CD上，然后在平面镜舳和CD之间来回反射，这时光

线的入射角等于反射角，即∠l=∠6，∠5=∠3，∠2=∠4．若已知∠l=55o，∠3=75o，那么∠2等于 ( )

A．50o B．55 o C．66 o D 65 o

三、解答题(8题，共64分)

13．(本题6分)如图所示，求∠A+∠B+∠C+∠D+∠E+∠F的度数．

14．(本题6分)已知：在△ABC中，∠A+∠B=2∠C，∠A—∠B=20o，求三角形三

个内角的度数．

15．(本题8分)如图，∠A=65o，∠ABD=30o，∠ACB=72o，且CE平分∠ACB，求

∠BEC的度数．

16．(本题8分)如果一个n边形的内角都相等，且它的每一个外角与内角的比为2：3，

求这个多边形的内角和．

17．本题8分)如果一个多边形的每个内角都相等，每个内角与每个外角的差是90o，求

这个多边形的内角和．

18．(本题8分)如图，在∆ABC中，∠B、∠C的平分线交于点O．

(1)若∠A=50o，求∠BOC的度数．

(2)设∠A=no(n为已知数)，求∠BOC的度数．

(3)当∠A为多少度时，∠BOC=3∠A?

19．(本题10分)一个同学在进行多边形的内角和计算时，所得的内角和为1125o，当发现错了以后，重新检测发现少了一个内角，问这个内角是多少度，他所求的是几边形的内角和?

20．(本题10分)连接多边形不相邻的两个顶点的线段，叫做多边形的对角线，如图(1)，

AC、AD是五边形ABCDE的对角线．思考下列问题：

(1)如图(2)n边形A1，A2，A3…An中，过顶点A1可以画______条对角线，它们分别

是________；过顶点A2可以画________条对角线，过顶点A3可以画条对角线．

(2)过顶点A1的对角线与过顶点A2的对角线有相同的吗?过顶点A1的对角线与过顶点A3的对角线有相同的吗?

(3)在此基础上，你能发现竹边形的对角线条数的规律吗?

参考答案

一、填空题

1．100o

2．80o

3．钝角

4．140o

5．6

6．5：3：1

二、选择题

7．A 8．D 9．C 10．C 11．B 12．D

三、解答题

13．360o

14．∠A=70o、∠B=50 o、∠C=60 o

15．∠BEC=131o

16．540o

17．1080o

18．(1) ∠BOC=115o

(2) ∠BOC=90o+1on 2

(3) ∠A=36o 19．135o 九边形

20．(1)n-3 A1A3、AlA4、A1A5、…、A1An-1

(2)没有对角线相同

(3)n(n3)

2

有一条对角线相同(即A1A3),

本文来源：http://www.guakaob.com/xiaoxue/504459.html