人教版七年级下数学各章典型类型题

【www.guakaob.com--一年级】

人教版七年级下数学各章典型类型题(一)
2015人教版七年级下册数学各章经典复习题

第五章 相交线与平行线

一、选择题

1、如图1，如果AB∥CD，那么下面说法错误的是（ ）

A．∠3=∠7； B．∠2=∠6 C、∠3+∠4+∠5+∠6=1800 D、∠4=∠8 2、如图2，AB∥DE，E65，则BC（ ）

A．135





A．180 B．270 C．360 D．540

10、已知：如图6，AB//CD，则图中、、三个角之间的数量关系为（ ）.

A、++=360 B、++=180 C、+-=180 D、--=90

P 2

M 1

a



B．115 C．36



D．65

）的长



3 b

N

3、如图3，PO⊥OR，OQ⊥PR，则点O到PR所在直线的距离是线段（

A、PO

B、RO

C、OQ D、PQ

图4 图5

C

二、填空题

11、把“等角的补角相等”写成“如果…，那么…”形式

A

A

F

B E

12、如图7，已知AB∥CD，BE平分∠ABC，∠CDE＝150°，则∠C＝

图3

B

D

图2

13、如图8，把长方形纸片沿14、如图9，已知

折叠，使，分别落在，的位置，若，则等于

图1

，=____________

4、下列语句：①直线外一点到这条直线的垂线段叫做点到直线的距离；②若两条直线被第三条截，则

D

C

内错角相等；③过一点有且只有一条直线与已知直线平行，真命题有（ ）个 A．1 B．2 C．3

D．以上结论皆错

5、如果a∥b，b

∥c

，那么a∥c，这个推理的依据是（

）

A、等量代换 B、两直线平行，同位角相等 C、平行公理 D、平行于同一直线的两条直线平行 6、如图4，小明从A处出发沿北偏东60°方向行走至B处，又沿北偏西20方向行走至C处，此时需把方向调整到与出发时一致，则方向的调整应是（ ）

A．右转80° B．左转80° C．右转100° D．左转100°

7、如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30，那么这两个角是（ ）

42、13842、13842、1010 A． ；B． 都是；C． 或；D． 以上都不对



A

B

图7 图8 图9 三、解答题 15、推理填空：

如图： ① 若∠1=∠2，则 ∥ （ ） 若∠DAB+∠ABC=1800，则 ∥ （ ） ②当 ∥ 时，∠ C+∠ABC=180°（ ） 当 ∥ 时，∠3=∠C（ ） 16．已知，如图∠1=∠ABC=∠ADC，∠3=∠5，∠2=∠4，∠ABC+∠BCD=180°． 将下列推理过程补充完整： （1）∵∠1=∠ABC（已知）， ∴AD∥______

（2）∵∠3=∠5（已知）， ∴AB∥______,

- 1 -



D

3

C

A

B

8、下列语句错误的是（ ）

A．连接两点的线段的长度叫做两点间的距离； B．两条直线平行，同旁内角互补 C．若两个角有公共顶点且有一条公共边，和等于平角，则这两个角为邻补 D．平移变换中，各组对应点连成两线段平行且相等

9、如图5，a∥b，M，N分别在a，b上，P为两平行线间一点，那么123（ ）

（_______________________________） （3）∵∠ABC+∠BCD=180°（已知）， ∴_______∥________,

（________________________________）

17、已知：如图AB∥CD，EF交AB于G，交CD于F，FH平分∠EFD，交AB于H ，∠AGE=500，第六章 实数

一、填空题

1

1.169的算术平方根为（ ）

求：∠BHF的度数．(8分) E A

H

B

CFD

18、已知，如图，CD⊥AB，GF⊥AB，∠B＝∠ADE，试说明∠1＝∠2． A

D

1E

F

B G

C

2、已知5的整数数部分为m，5的小数部分为n，则mn（ ） 3、式子x3有意义，x的取值范围（ ）

4、已知：y=x5+x+3,则xy的值为（ ）

5、

3a40

，求a+b的值（ ）

6、9的平方根是 （ ） 7、快速地表示并求出下列各式的平方根

9

⑴116 ⑵|－5| ⑶0.81 ⑷（－9）2

8、如果一个数的平方根是a1和2a7，求这个数？

9.用平方根定义解方程

⑴16（x+2）2=81 ⑵4x2-225=0

10、下列说法正确的是( )

A、的平方根是4 B、6表示6的算术平方根的相反数

C、 任何数都有平方根 D、a2一定没有平方根

11、求值：

⑴0.512 ⑵－729= ⑶

(2)3

= ⑷（）3=

12、如果x2有意义，x的取值范围为

- 2 -

13.用立方根的定义解方程

⑴x3-27 =0 ⑵2（x+3）3=512

已知31.732，5.477

300 ；（2）0.3 ；

（3）0.03的平方根约为 ；（4）若x54.77，则x

已知31.442，3.107，6.694，

求（1）.3 ；（2）3000的立方根约为 （3）x31.07，则x 重要公式 公式一: ∵

22=

32

42= (2)2

(3)2

= (4)2

=

∴a2

(1

有关练习： 1.7)2

= 22.如果(a3)2

=a-3，则a的取值范围是； 如果

(a3)2

=3-a,则a的取值范围是

3.数a,b在数轴上的位置如图： 化简：

(ab)2

+|c+a|

公式二： ∵（4）2= （）2= （25）2=

∴(a)2

= (a≥0)

综合公式一和二，可知，当满足a 条件时，a2

=(a)2

公式三： ∵ 23

33

43

(2)3

(3)3

(4)3

∴a3；

随堂练习：化简：当1＜a＜3时，(1a)2

+

(a3)3

公式四： ∵ （）3= （27）3= （）3= ∴(a)3综合公式三和四，可知，当满足a 条件时，a3

=(a)3

公式五：

3

a

知识点五：实数定义及分类

无理数的定义： 实数的定义： 实数与上的点是一一对应的 1、判断下列说法是否正确：

（1）实数不是有理数就是无理数 （2）无限小数都是无理数。 （3）无理数都是无限小数。 （4）根号的数都是无理数。

（5）两个无理数之和一定是无理数。（6）所有的有理数都可以在数轴上表示，反过来，数轴上所有的

点都表示有理数。

2、把下列各数中，有理数为；无理数为 ,  ,52,2,20

3, ,3.14, ,  ,0.030030003........

3、大于而小于的所有整数为 知识点六：实数的有关运算 计算

3



（结果精确到0.01）

- 3 -

2、已知a、b、c位置如图所示， 化简 ：

a2abca

8．线段CD是由线段AB平移得到的，点A(-1,4)的对应点为C(4,7),则点B(-4,-1)的对应点D的坐标是（ ）

bc2

A．(2,9) B．(5,3) C．(1,2) D．(-9,-4)

9.如图，把图○1中△ABC经过一定的变换得到图○2中的△ABC，如果图○1的△ABC上点P的坐标是

'(a,b)，那么这个点在图○2中的对应点P的坐标是 （ ）

'

'

'

(a2,b3) B．(a2,b3) C．(a3,b2) D．(a2,b3)

第七章 平面直角坐标系

一、选择题

1．若a0，则点P(a,2)应在 （ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限

2

(1,m1)一定在 （ ） 2．在平面直角坐标系中，点P

10．点P(2,-3)先向上平移2个单位长度，再向左平移3个单位长度，得到点P的坐标是（ ） A．(-1,-5) B．(-1,-1) C．(5,-1) D．(5,5) 二、填空题

1．在坐标系内，点P（2,－2）和点Q（2,4）之间的距离等于________个单位长度，线段PQ的中点坐标是____________

2．将点M(2,-3)向左平移2个单位长度，再向下平移1个单位长度，得到的点的坐标为_______ 3.在直角坐标系中，若点P(a2,b5)在y轴上，则点P的坐标为____________ 4．已知点P(2,a)，Q(b,3)，且PQ∥x轴，则a_________，b___________

5．将点P(3,y)向下平移3个单位，并向左平移2个单位后得到点Q(x,1)，则xy=_________ 6.则坐标原点O（0,0），A（-2,0）,B(-2,3)三点围成的△ABO的面积为____________ 7．点P(a,b)在第四象限，则点Q(b,a)在第______象限

'

A．第一象限 B．第二象限 C．第三象限 D．第四象限

3．在平面直角坐标系中，线段BC∥x轴，则 （ ） A．点B与C的横坐标相等 B．点B与C的纵坐标相等 C．点B与C的横坐标与纵坐标分别相等 D．点B与C的横坐标、纵坐标都不相等

4．若点P(x,y)的坐标满足xy0则点P必在 （ ）A．原点 B．x轴上 C．y轴上 D．x轴或y轴上

5．点P在x轴上 ，且到y轴的距离为5，则点P的坐标是 （ ） A．(5,0) B．(0,5) C．(5,0)或(-5,0) D．(0,5)或(0,-5)

6.平面上的点(2,-1)通过上下平移不能与之重合的是 （ ） A．(2,-2) B．(-2,-1) C．(2,0) D．2,-3)

7.将△ABC各顶点的横坐标分别减去3，纵坐标不变，得到的△ABC相应顶点的坐标，则△ABC可以看成△ABC （ ） A．向左平移3个单位长度得到 B．向右平移三个单位长度得到 C．向上平移3个单位长度得到 D．向下平移3个单位长度得到

- 4 -

'

'

'

'

'

'

8．已知点P在第二象限两坐标轴所成角的平分线上，且到x轴的距离为3，则点P的坐标为____________ 9．在同一坐标系中，图形a是图形b向上平移3个单位长度得到的，如果在图形a中点A的坐标为(5,

3)，则图形b中与A对应的点A的坐标为__________

'

10．已知线段AB=3，AB∥x轴，若点A的坐标为（1,2）,则点B的坐标为_________________ 三、解答题

如图，在平面直角坐标系中，分别写出△ABC的顶点坐标，并求出△ABC的面积。

第八章 二元一次方程组

1．下列方程组是二元一次方程组的是（ ）．



xy1

B.

4xy1xy2

C.

x2x20D.1

x1y A．

y2x3

yx1

3xy0

二元一次方程2xy7的正整数解有（ ）个。 A. 1 B. 2 C. 3 D. 4

5xy3x2y5

3. 已知方程组ax5y4和5xby1有相同的解，则a，b的值为 （ ） a1a4



a6

a14Ａ．b2 Ｂ．b6

Ｃ．b2 Ｄ．b2

4．买钢笔和铅笔共30支，其中钢笔的数量比铅笔数量的2倍少3支．若设买钢笔x支，铅笔y支，根据题意，可得方程组（ ）．

xy30xy30

A．y2x3 B．y2x3 

xy30

xy30C．x2y3 D．

x2y3

5、已知甲、乙两人的年收入之比为2：3，年支出之比为4：7，年终时两人都余了400元，若设甲的年收入为x元，年支出为y元，则可列方程组( )



xy4002

xy400

x7y400A34 32x47y400 B

xy400xy400

2x4

y4003x7C37 D．24y400

6、已知二元一次方程

3x

1

2y1＝0，用含x的代数式表示y为



4x3y14

7. 若方程组kx(k1)y6的解中x、y的值相等，k

- 5 -

人教版七年级下数学各章典型类型题(二)
人教版七年级下册数学各章知识点及练习题

第一讲 相交线与平行线

1. 两直线相交所成的四个角中，有一条公共边，它们的另一边互为反向延长线，具有这种

关系的两个角，互为_____________.

2. 两直线相交所成的四个角中，有一个公共顶点，并且一个角的两边分别是另一个角两边

的反向延长线，具有这种关系的两个角，互为------________对顶角的性质：______ ______

3. 两直线相交所成的四个角中，如果有一个角是直角，那么就称这两条直线相互_______.

垂线的性质：⑴过一点______________一条直线与已知直线垂直. ⑵连接直线外一点与直线上各点的所在线段中，_______________. 4. 直线外一点到这条直线的垂线段的长度，叫做________________________.

5. 两条直线被第三条直线所截，构成八个角，在那些没有公共顶点的角中，⑴如果两个角

分别在两条直线的同一方，并且都在第三条直线的同侧，具有这种关系的一对角叫做___________ ；⑵如果两个角都在两直线之间，并且分别在第三条直线的两侧，具有这种关系的一对角叫做____________ ；⑶如果两个角都在两直线之间，但它们在第三条直线的同一旁，具有这种关系的一对角叫做_______________.

6. 在同一平面内，不相交的两条直线互相___________.同一平面内的两条直线的位置关系

只有________与_________两种.

7. 平行公理：经过直线外一点，有且只有一条直线与这条直线______.

推论：如果两条直线都与第三条直线平行，那么_____________________. 8. 平行线的判定：⑴_____________________________________.

⑵___________________________ ⑶__________________________________. 9. 平行线的性质：⑴ ＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.

（2）_______________________________.⑶__________________________________ . 10. 把一个图形整体沿某一方向移动，会得到一个新图形，图形的这种移动，叫做_______.

平移的性质：⑴把一个图形整体平移得到的新图形与原图形的形状与大小完全______. ⑵新图形中的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点.连接各组对应点的线段_________________.

11.判断一件事情的语句，叫做_______.命题由________和_________两部分组成。命题常可

以写成“如果„„那么„„”的形式。

一、对顶角与邻补角的概念及性质

1、如图所示,∠1和∠2是对顶角的图形有( )【人教版七年级下数学各章典型类型题】

2、下列说法正确的有( ) A.1个 B.2个 C.3个 D.4个

①对顶角相等;②相等的角是对顶角;③若两个角不相等,则这两个角一定不是对顶角;④若两个角不是对顶角,则这两个角不相等。

3、如图1，AB与CD相交所成的四个角中,∠1的邻补角是______,∠1的对顶角 若∠1=25°,则∠2=_______,∠3=______,∠4=_______

4、如图2，直线AB,CD,EF相交于点O,则∠AOD的对顶角是_____,∠AOC的邻补角是_______;

若∠AOC=50°,则∠BOD=______,∠COB=_______

5、如图3，AB,CD,EF交于点O,∠1=20°,∠BOC=80°,则∠2的度数 6、如图4，直线AB和CD相交于点O,若∠AOD与∠BOC的和为236°,则∠AOC•的度数为( )

①若∠AOD-∠DOB=70,则∠BOC=_____,∠DOB=____ ②若∠AOC:∠AOD=2:3,则∠BOD的度数

7、如图5,直线AB,CD相交于点O,已知∠AOC=70°,且∠BOE:∠EOD=2:3, 则∠EOD=________ 1

AC

24

图1

E

D

F

DB

AC

图2

A

B

图3

BF

A

A

DB

D

O

图5

C

图4

EB

D

二、会识别同位角、内错角、同旁内角

C

1、如图1，∠1和∠4是AB和∠3和∠5是、 被 所截得的 角，∠2和∠5是 、 所截得的 角，AC、BC被AB所截得的同旁内角是

2、如图2，AB

、

DC

被

BD所截得的内错角是 ，AB、CD被AC所截是的内错角是 ，AD、BC被BD所截得的内错角是 ，AD、BC被AC所截得的内错角是 3、如图3，直线AB、CD被DE所截，则∠1和 是同位角，∠1和 是内错角，∠1和 是同旁内角，如果∠1=∠5.那么∠1 ∠3.

图1

图2

图3

4、下列所示的四个图形中，和 ）

A. ②③ B. ①②③ C. ①②④ D. ①④

三、垂直

1、如图，BCAC,CB8cm,AC6cm,AB10cm,那么点A到BC的距离是_____，点B到AC的距离是_______，点A、B两点的距离是_____，点C到AB的距离是________．

2、如图，已知AB、CD、EF相交于点O，AB⊥CD，OG平分∠AOE，∠FOD＝28°，求∠COE、∠AOE、∠AOG的度数。

3、如图，AOC与BOC是邻补角，OD、OE分别是AOC与BOC的平分线，试判断OD与OE的位置关系，并说明理由。

四、平行线的判定

1、下列图形中，直线a与直线b平行的是（ ）

2、如图，已知

1C

D

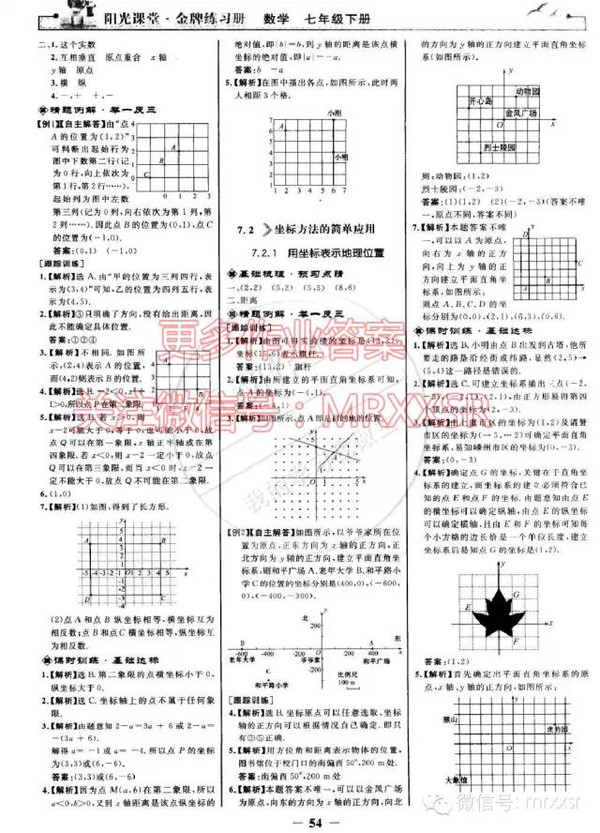
AB∥CD, ∠1=∠3, 试说明AC∥BD.

A2

B3

3、如图，已知AB∥CD，∠1＝∠2，试说明EP∥FQ． 证明：∵AB∥CD，

∴∠MEB＝∠MFD（ ） 又∵∠1＝∠2，

∴∠MEB－∠1＝∠MFD－∠2， 即 ∠MEP＝∠______

∴EP∥_____．（ ）

4、如图，已知∠BAF＝50°，∠ACE＝140°，CD⊥CE，能判断DC∥AB吗？为什么？ F

D

C

A

B

E

5、已知∠B＝∠BGD，∠DGF＝∠F，求证：AB∥EF。

五、平行线的性质

1、已知AB∥CD，∠A＝70°，则∠1的度数是（ ）

A．70° B．100° C．110° D．130°

2、如图2，AB∥DE，E65，则BC（ ） A．135

B．115 C．36 D．

65

1

D B

3、如图，已知AB∥CD，BE平分∠ABC，∠CDE＝150°，则∠C＝______

A

E

D

C

D【人教版七年级下数学各章典型类型题】

B

E B C

4、如图，∠CAB＝100°，∠ABF＝110°，AC∥PD，BF∥PE，求∠DPE的度数。

5、如图，AB∥CD,AD∥BC,∠A=3∠B.求∠A、∠B、∠C、∠D的度数.

6、如图，已知AB//CD，=____________

C六、平行线性质与判定的综合应用 A

1、如图1，∠B=∠C，AB∥EF 求证：∠BGF=∠C

DF

2、如图2，已知∠1=∠3，∠P=∠T。求证：∠M=∠R．

3、如图3，AB∥DE，∠1＝∠ACB，AC平分∠BAD， (1) 试说明: AD∥BC．

(2) 若∠B=80°，求：∠ADE的度数。

4、已知：如图,DE⊥AO于E,BO⊥AO,FC⊥AB于C，∠1=∠2,求证：DO⊥AB. 5、如图，已知ABC，ADBC于D，E为AB上一点，EFBC于F，DG//BA交CA于G.求证12

E

人教版七年级下数学各章典型类型题(三)
2016人教版七年级下册数学各章经典复习题_整理

第五章 相交线与平行线

一、选择题

1、如图1，如果AB∥CD，那么下面说法错误的是（ ）

A．∠3=∠7； B．∠2=∠6 C、∠3+∠4+∠5+∠6=1800 D、∠4=∠8 2、如图2，AB∥DE，E65，则BC（ ）

A．135





B．115 C．36



D．65

）的长



3、如图3，PO⊥OR，OQ⊥PR，则点O到PR所在直线的距离是线段（

A、PO

A

B、RO

C、OQ D、PQ

B

E 图

D

7

3

B

图

图

4、下列语句：①直线外一点到这条直线的垂线段叫做点到直线的距离；②若两条直线被第三条截，则内错角相等；③过一点有且只有一条直线与已知直线平行，真命题有（ ）个 A．1 B．2 C．3 D．以上结论皆错 5、如果a∥b，b∥c，那么a∥c，这个推理的依据是（ ）

A、等量代换 B、两直线平行，同位角相等 C、平行公理 D、平行于同一直线的两条直线平行

6、如图4，小明从A处出发沿北偏东60°方向行走至B处，又沿北偏西20方向行走至C处，此时需把方向调整到与出发时一致，则方向的调整应是（ ）

A．右转80° B．左转80° C．右转100° D．左转100°

7、如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30，那么这两个角是（ ）

42、13842、13842、1010 A． ；B． 都是；C． 或；D． 以上都不对



8、下列语句错误的是（ ）

A．连接两点的线段的长度叫做两点间的距离； B．两条直线平行，同旁内角互补 C．若两个角有公共顶点且有一条公共边，和等于平角，则这两个角为邻补 D．平移变换中，各组对应点连成两线段平行且相等

9、如图5，a∥b，M，N分别在a，b上，P为两平行线间一点，那么123（ ）

A．180 B．270 C．360 D．540

10、已知：如图6，AB//CD，则图中、、三个角之间的数量关系为（ ）.

A、++=360 B、++=180 C、+-=180 D、--=90

图

1

a b





N 图

二、填空题

11、把“等角的补角相等”写成“如果…，那么…”形式 12、如图7，已知AB∥CD，BE平分∠ABC，∠CDE＝150°，则∠C＝

C分别落在D，C的位置，13、如图8，把长方形纸片沿EF折叠，使D，若∠EFB65，则∠AED



等于

14、如图9，已知AB//CD，=____________

A

B

图7 图8 图9 三、解答题 15、推理填空：

如图： ① 若∠1=∠2，则 ∥ （ 23

1

D

C

若∠DAB+∠ABC=1800，则 ∥ （ ） ②当 ∥ 时，∠ C+∠ABC=180°（ ） 当 ∥ 时，∠3=∠C（ ） 16．已知，如图∠1=∠ABC=∠ADC，∠3=∠5，∠2=∠4，∠ABC+∠BCD=180°． 将下列推理过程补充完整： （1）∵∠1=∠ABC（已知）， ∴AD∥______

A

B

（2）∵∠3=∠5（已知）， ∴AB∥______,

（_______________________________） （3）∵∠ABC+∠BCD=180°（已知）， ∴_______∥________,

（________________________________）

17、已知：如图AB∥CD，EF交AB于G，交CD于F，FH平分∠EFD，交AB于H ，∠AGE=500，求：∠BHF的度数．(8分)

CEA

H

B

FD

18、已知，如图，CD⊥AB，GF⊥AB，∠B＝∠ADE，试说明∠1＝∠2．

A

BF

D

1

E

G

C

第六章 实数

一、填空题

1

1.169的算术平方根为（ ）

2、已知5的整数数部分为m，5的小数部分为n，则mn（ ） 3、式子x3有意义，x的取值范围（ ）

4、已知：y=x5+x+3,则xy的值为（ ） 5、

3a40

，求a+b的值（ ）

6、9的平方根是 （ ） 7、快速地表示并求出下列各式的平方根

9

⑴116 ⑵|－5| ⑶0.81 ⑷（－9）2

8、如果一个数的平方根是a1和2a7，求这个数？

9.用平方根定义解方程

⑴16（x+2）2=81 ⑵4x2-225=0

10、下列说法正确的是( )

A、的平方根是4 B、6表示6的算术平方根的相反数

2aC、 任何数都有平方根 D、一定没有平方根

11、求值：

⑴0.512 ⑵－729= ⑶

(2)3

= ⑷（）3=

12、如果x2有意义，x的取值范围为

13.用立方根的定义解方程

⑴x3-27 =0 ⑵2（x+3）3=512

已知31.732，5.477

300 ；（2）0.3 ；

（3）0.03的平方根约为 ；（4）若x54.77，则x

已知31.442，3.107，3006.694， 求（1）0.3 ；（2）3000的立方根约为

（3）x31.07，则x 重要公式 公式一: ∵

(2)2

22=

(3)2

32

(4)2

42= = =

2

a∴

1

()2

7= 2有关练习： 1.2.如果 如果

(a3)2

=a-3，则a的取值范围是； =3-a,则a的取值范围是

(a3)2

3.数a,b在数轴上的位置如图： 化简：

(ab)2

+|c+a|

公式二： ∵（4）2= （）2= （25）2=

2

(a)∴= (a≥0)

22

(a)a综合公式一和二，可知，当满足a 条件时，=

3

公式三： ∵

23 (2)3

33

(3)3

3

43 (4)3

人教版七年级下数学各章典型类型题(四)
2013人教版七年级下册数学各章经典复习题

第五章 相交线与平行线

一、选择题

1、如图1，如果AB∥CD，那么下面说法错误的是（ ）

A．∠3=∠7； B．∠2=∠6 C、∠3+∠4+∠5+∠6=1800 D、∠4=∠8 2、如图2，AB∥DE，E65，则BC（ ）

A．135

B．115 C．36

BA

A

B E

D．65 图1 图2 图3

）的长 A、PO

B、RO

C、OQ

D、PQ

3、如图3，PO⊥OR，OQ⊥PR，则点O到PR所在直线的距离是线段（

4、下列语句：①直线外一点到这条直线的垂线段叫做点到直线的距离；②若两条直线被第三条截，则内错角相等；③过一点有且只有一条

直线与已知直线平行，真命题有（ ）个 A．1 B．2 C．3 D．以上结论皆错

5、如果a∥b，b∥c，那么a∥c，这个推理的依据是（ ）

A、等量代换 B、两直线平行，同位角相等 C、平行公理 D、平行于同一直线的两条直线平行 6、如图，小明从A处出发沿北偏东60°方向行走至B处，又沿北偏西20方向行走至C处，此时需把方向调整到与出发时一致，则方向的调整应是（ ）A．右转80° B．左转80° C．右转100° D．左转100°

7、如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30，那么这两个角是（ ） A． 42、138；B． 都是10；C． 42、138或42、10；D． 以上都不对

8、下列语句错误的是（ ）A．连接两点的线段的长度叫做两点间的距离； B．两条直线平行，同旁内角互补





M 1

P 2

3

N

b

C．若两个角有公共顶点且有一条公共边，和等于平角，则这两个角为邻补D．平移变换中，各组对应点连成两线段平行且相等

9、如图7，a∥b，M，N分别在a，b上，P为两平行线间一点，那么123（ ）A．180 B．270 C．360 D．540





10、已知：如图，AB//CD，则图中、、三个角之间的数量关系为（ ）.

D、--=90

三、解答题 15、推理填空：

如图： ① 若∠1=∠2，则 ∥ （ ） 若∠DAB+∠ABC=180，则 ∥ （ ）0

3

C

②当 ∥ 时，∠ C+∠ABC=1800 （ ） 当 ∥ 时，∠3=∠C（ ） A

B

16．已知，如图∠1=∠ABC=∠ADC，∠3=∠5，∠2=∠4，∠ABC+∠BCD=180°． 将下列推理过程补充完整： （1）∵∠1=∠ABC（已知）， ∴AD∥______

（2）∵∠3=∠5（已知）， ∴AB∥______,

（_______________________________） （3）∵∠ABC+∠BCD=180°（已知）， ∴_______∥________,

（________________________________） 18、已知，如图，CD⊥AB，GF⊥AB，∠B＝∠ADE，试说明∠1＝∠2．

A

D

E

FB

G

C

第六章 实数

有关练习： 1.()

17

2

22

11112.如果(a3)=a-3，则a的取值范围是 1.的算术平方根为（ ）（A） （B）－ （C）± 169131313

2

2、已知5的小数部分为m，5的小数部分为n，则mn 如果(a3)=3-a,则a的取值范围是3、式子x3有意义，x的取值范围4、已知：y=x5+5x+3,则xy的值为 5、3a40，求a+b的值 6、9的平方根是7、快速地表示并求出下列各式的平方根

⑴1

9

16

⑵|－5| ⑶0.81 ⑷（－9）2

8、如果一个数的平方根是a1和2a7，求这个数？

9.用平方根定义解方程

⑴16（x+2）2=81 ⑵4x2-225=0 10、下列说法正确的是( )

A、的平方根是4 B、6表示6的算术平方根的相反数

C、 任何数都有平方根 D、a2

一定没有平方根 11、求值：

⑴0.512 ⑵－729 ⑶(2)3

⑷（）3

12、如果x2有意义，x的取值范围为 13.用立方根的定义解方程

⑴x3-27 =0 ⑵2（x+3）3=512

14、已知31.732，5.477

（1） ；（2）0.3 ；

（3）0.03的平方根约为 ；（4）若x54.77，则x 2、已知1.442，303.107，3006.694， 求（1）0.3；（2）3000的立方根约为 ； （3）x31.07，则x 重要公式 公式一: ∵

22

32 42(2)2

(3)2

(4)2

∴a2 =

3.数a,b在数轴上的位置如图： 化简：(ab)2

+|c+a|

公式二： ∵（4）2 （9）2 （25）2

∴(a)2= (a≥0)

综合公式一和二，可知，当满足a 条件时，

a2=(a)2

公式三： ∵ 23

33 43

(2)3

(3)3

(4)3

∴a3

= ；

随堂练习：化简：当1＜a＜3时，(1a)2 +(a3)3

公式四： ∵ （）3 （27）3 （）3= ∴(a)3=

综合公式三和四，可知，当满足a a3

=(a)3 公式五：

a= 知识点五：实数定义及分类

无理数的定义： 实数的定义： 实数与 上的点是一一对应的

1、判断下列说法是否正确：

（1）实数不是有理数就是无理数 （2）无限小数都是无理数。 （3）无理数都是无限小数。 （4）根号的数都是无理数。 （5）两个无理数之和一定是无理数。（6）所有的有理数都可以在数轴上表示，反过来，数轴上所有的点都表示有理数。

2、把下列各数中，有理数为 ；无理数为 ,  ,52,2,20

3

,36 ,3.14, ,  ,0.030030003........

3、大于而小于的所有整数为

知识点六：实数的有关运算 1、计算

3 （结果精确到0.01）

2、已知a、b、c位置如图所示，

化简 ：a2

abca

bc2

第七章 平面直角坐标系

一、选择题

4．已知点P(2,a)，Q(b,3)，且PQ∥x轴，则a_________，

b___________

1．若a0，则点P(a,2)应在 （ ）

5．将点P(3,y)向下平移3个单位，并向左平移2个单位后得到点

A．第一象限 B．第二象限 C．第三象限 D．第四象限

Q(x,1)，则xy=_________

2．在平面直角坐标系中，点P(1,m21)一定在

6.则坐标原点O（0,0），A（-2,0）,B(-2,3)三点围成的△ABO的面

（ ）

积为____________

A．第一象限 B．第二象限 C．第三象限 D．第四象限

7．点P(a,b)在第四象限，则点Q(b,a)在第______象限 3．在平面直角坐标系中，线段BC∥x轴，则（ ）

8．已知点P在第二象限两坐标轴所成角的平分线上，且到x轴的距

A．点B与C的横坐标相等 B．点B与C的纵坐标相等

离为3，则点P的坐标为____________

C．点B与C的横坐标与纵坐标分别相等

9．在同一坐标系中，图形a是图形b向上平移3个单位长度得到的，

D．点B与C的横坐标、纵坐标都不相等

如果在图形a中点A的坐标为(5,3)，则图形b中与A对应的点A'的

4．若点P(x,y)的坐标满足xy0则点P必在（ ）A．原点 B．x轴上 C．y轴上 D．x轴或y轴上 5．点P在x轴上 ，且到y轴的距离为5，则点P的坐标是（ ）

A．(5,0) B．(0,5) C．(5,0)或(-5,0) D．(0,5)或(0,-5)

6.平面上的点(2,-1)通过上下平移不能与之重合的是（ ）

A．(2,-2) B．(-2,-1) C．(2,0) D．2,-3)

7.将△ABC各顶点的横坐标分别减去3，纵坐标不变，得到的△A'B'C'

相应顶点的坐标，则△A'B'C'可以看成△（ ）

A．向左平移3个单位长度得到 B．向右平移三个单位长度得到

C．向上平移3个单位长度得到 D．向下平移3个单位长度得到

8．线段CD是由线段AB平移得到的，点A(-1,4)的对应点为C(4,7),

则点B(-4,-1)的对应点D的坐标是（ ）A．(2,9) B．(5,3) C．(1,2) D．(-9,-4)

9.如图，把图○1中△ABC经过一定的变换得到图○2中的

△A'

B'

C'

，如果图○1的△ABC上点P的坐标是(a,b)，那么这个点在

图○2中的对应点P'的坐标是 （ ） A．(a2,b3) B．(a2,b3) C．(a3,b2) D．(a2,b3)

10．点P(2,-3)先向上平移2个单位长度，再向左平移3个单位长度，得到点P'的坐标是（ ）

A．(-1,-5) B．(-1,-1) C．(5,-1) D．(5,5) 二、填空题 1．在坐标系内，点P（2,－2）和点Q（2,4）之间的距离等于________个单位长度，线段PQ的中点坐标是____________ 2．将点M(2,-3)向左平移2个单位长度，再向下平移1个单位长度，得到的点的坐标为_______

3.在直角坐标系中，若点P(a2,b5)在y轴上，则点P的坐标为

坐标为__________

10．已知线段AB=3，AB∥x轴，若点A的坐标为（1,2）,则点B的

坐标为_________________

三、解答题

如图，在平面直角坐标系中，分别写出△ABC的顶点坐标，并求

出△ABC的面积。

第八章 二元一次方程组

1．下列方程组是二元一次方程组的是（ ）．

A．xy14xy1x2x201

1xy2B.y2x3C.D.yx1xy 3xy0

2. 二元一次方程2xy7的正整数解有（ ）个。 A. 1 B. 2 C. 3 D. 4

3. 已知方程组5xy3ax5y4和x2y5xby1

有相同的解，则a，b的值

5为 （ ）

Ａ．a1 Ｂ．a4a6a14b2 Ｃ．b6 Ｄ．b2

2

b4．买钢笔和铅笔共30支，其中钢笔的数量比铅笔数量的2倍少3

支．若设买钢笔x支，铅笔y支，根据题意，可得方程组（ ）． A．xy30xy30y2x3 B．y2x3 C．xy30xy30x2y3 D． 

x2y3

5、已知甲、乙两人的年收入之比为2：3，年支出之比为4：7，年

终时两人都余了400元，若设甲的年收入为x元，年支出为y元，

则可列方程组( )

xy400xy4002x7y4003x4A34 B 27y400 xy400xy400

2x437C37y400 D．2x4y400 6. 已知二元一次方程3x12y1＝0，用含x的代数式表示y为

7. 若方程组4x3y14

(k1)y6的解中x、y的值相等，kkx8、甲、乙二人同解方程组axby2x3y2，甲正确解得1

，乙因

cxy1抄错了c，解得x2

y6，则abc= 9. 已知3x2y17

2x3y13，则x-y= 。 10.若满足方程组3x5ym2

的x

2x3ym，y的值的和等于6，则m的值为 ． 11. 已知3a2b4,2ab5,则85ab____.

12.若3xy52

2xy30，则xy_______。

13．姐姐4年前的年龄是妹妹年龄的2倍，今年年龄是妹妹的1.5倍，则姐姐今年的年龄是 岁。

4(xy1)3(1y)2

14. （8分）解方程组

x2y3

2

15．已知y=x2+px+q，当x=1时，y的值为2；当x=-2时，y的值为

2．求当x=-3时，y的值．

16.上杭县某中学七年级学生外出进行社会实践活动，如果每辆车坐45人，那么有15个学生没车坐；如果每辆车坐60人，那么可以空出一辆车。问共有几辆车，几个学生？

17．甲、乙两人练习跑步，如果甲让乙先跑10米，甲跑5秒钟就可

追上乙；如果甲让乙先跑2秒钟，甲跑4秒钟就能追上乙．求甲乙两人的速度．

18. 服装厂要生产一批某种型号的学生服装，已知3米长的布料可

做上衣2件或裤子3条，一件上衣和一条裤子为一套，计划用600

米长的这种布料生产，应分别用多少布料生产上衣和裤子才能恰好

配套？共能生产多少套？

人教版七年级下数学各章典型类型题(五)
2016人教版七年级下册数学各章经典复习题

一．第五章 相交线与平行线

一、选择题

1、如图1，如果AB∥CD，那么下面说法错误的是（ ）

A．∠3=∠7； B．∠2=∠6 C、∠3+∠4+∠5+∠6=1800 D、∠4=∠8 2、如图2，AB∥DE，E65，则BC（ ）

A．135

B．115 C．36

BA

A

B E

D．65 图1 图2 图3

）的长 A、PO

B、RO

C、OQ

D、PQ

3、如图3，PO⊥OR，OQ⊥PR，则点O到PR所在直线的距离是线段（

4、下列语句：①直线外一点到这条直线的垂线段叫做点到直线的距离；②若两条直线被第三条截，则内错角相等；③过一点有且只有一条

直线与已知直线平行，真命题有（ ）个 A．1 B．2 C．3 D．以上结论皆错

5、如果a∥b，b∥c，那么a∥c，这个推理的依据是（ ）

A、等量代换 B、两直线平行，同位角相等 C、平行公理 D、平行于同一直线的两条直线平行 6、如图，小明从A处出发沿北偏东60°方向行走至B处，又沿北偏西20方向行走至C处，此时需把方向调整到与出发时一致，则方向的调整应是（ ）A．右转80° B．左转80° C．右转100° D．左转100°

7、如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30，那么这两个角是（ ） A． 42、138；B． 都是10；C． 42、138或42、10；D． 以上都不对

8、下列语句错误的是（ ）A．连接两点的线段的长度叫做两点间的距离； B．两条直线平行，同旁内角互补





M 1

P 2

3

N

b

C．若两个角有公共顶点且有一条公共边，和等于平角，则这两个角为邻补D．平移变换中，各组对应点连成两线段平行且相等

9、如图7，a∥b，M，N分别在a，b上，P为两平行线间一点，那么123（ ）A．180 B．270 C．360 D．540





10、已知：如图，AB//CD，则图中、、三个角之间的数量关系为（ ）.

D、--=90

三、解答题 15、推理填空：

如图： ① 若∠1=∠2，则 ∥ （ ） 若∠DAB+∠ABC=180，则 ∥ （ ）0

3

C

②当 ∥ 时，∠ C+∠ABC=1800 （ ） 当 ∥ 时，∠3=∠C（ ） A

B

16．已知，如图∠1=∠ABC=∠ADC，∠3=∠5，∠2=∠4，∠ABC+∠BCD=180°． 将下列推理过程补充完整： （1）∵∠1=∠ABC（已知）， ∴AD∥______

（2）∵∠3=∠5（已知）， ∴AB∥______,

（_______________________________） （3）∵∠ABC+∠BCD=180°（已知）， ∴_______∥________,

（________________________________） 18、已知，如图，CD⊥AB，GF⊥AB，∠B＝∠ADE，试说明∠1＝∠2．【人教版七年级下数学各章典型类型题】

A

D

E

FB

G

C

二. 第六章 实数

有关练习： 1.()

17

2

22

11112.如果(a3)=a-3，则a的取值范围是 1.的算术平方根为（ ）（A） （B）－ （C）± 169131313

2

2、已知5的小数部分为m，5的小数部分为n，则mn 如果(a3)=3-a,则a的取值范围是3、式子x3有意义，x的取值范围4、已知：y=x5+5x+3,则xy的值为 5、3a40，求a+b的值 6、9的平方根是7、快速地表示并求出下列各式的平方根

⑴1

9

16

⑵|－5| ⑶0.81 ⑷（－9）2

8、如果一个数的平方根是a1和2a7，求这个数？

9.用平方根定义解方程

⑴16（x+2）2=81 ⑵4x2-225=0 10、下列说法正确的是( )

A、的平方根是4 B、6表示6的算术平方根的相反数

C、 任何数都有平方根 D、a2

一定没有平方根 11、求值：

⑴0.512 ⑵－729 ⑶(2)3

⑷（）3

12、如果x2有意义，x的取值范围为 13.用立方根的定义解方程

⑴x3-27 =0 ⑵2（x+3）3=512

14、已知31.732，5.477

（1） ；（2）0.3 ；

（3）0.03的平方根约为 ；（4）若x54.77，则x 2、已知1.442，303.107，3006.694， 求（1）0.3；（2）3000的立方根约为 ； （3）x31.07，则x 重要公式 公式一: ∵

22

32 42(2)2

(3)2

(4)2

∴a2 =

3.数a,b在数轴上的位置如图： 化简：(ab)2

+|c+a|

公式二： ∵（4）2 （9）2 （25）2

∴(a)2= (a≥0)

综合公式一和二，可知，当满足a 条件时，

a2=(a)2

公式三： ∵ 23

33 43

(2)3

(3)3

(4)3

∴a3

= ；

随堂练习：化简：当1＜a＜3时，(1a)2 +(a3)3

公式四： ∵ （）3 （27）3 （）3= ∴(a)3=

综合公式三和四，可知，当满足a a3

=(a)3 公式五：

a= 知识点五：实数定义及分类

无理数的定义： 实数的定义： 实数与 上的点是一一对应的

1、判断下列说法是否正确：

（1）实数不是有理数就是无理数 （2）无限小数都是无理数。 （3）无理数都是无限小数。 （4）根号的数都是无理数。 （5）两个无理数之和一定是无理数。（6）所有的有理数都可以在数轴上表示，反过来，数轴上所有的点都表示有理数。

2、把下列各数中，有理数为 ；无理数为 ,  ,52,2,20

3

,36 ,3.14, ,  ,0.030030003........

3、大于而小于的所有整数为

知识点六：实数的有关运算 1、计算

3 （结果精确到0.01）

2、已知a、b、c位置如图所示，

化简 ：a2

abca

bc2

三. 第七章 平面直角坐标系

一、选择题

4．已知点P(2,a)，Q(b,3)，且PQ∥x轴，则a_________，

b___________

1．若a0，则点P(a,2)应在 （ ）

5．将点P(3,y)向下平移3个单位，并向左平移2个单位后得到点

A．第一象限 B．第二象限 C．第三象限 D．第四象限

Q(x,1)，则xy=_________

2．在平面直角坐标系中，点P(1,m21)一定在

6.则坐标原点O（0,0），A（-2,0）,B(-2,3)三点围成的△ABO的面

（ ）

积为____________

A．第一象限 B．第二象限 C．第三象限 D．第四象限

7．点P(a,b)在第四象限，则点Q(b,a)在第______象限 3．在平面直角坐标系中，线段BC∥x轴，则（ ）

8．已知点P在第二象限两坐标轴所成角的平分线上，且到x轴的距

A．点B与C的横坐标相等 B．点B与C的纵坐标相等

离为3，则点P的坐标为____________

C．点B与C的横坐标与纵坐标分别相等

9．在同一坐标系中，图形a是图形b向上平移3个单位长度得到的，

D．点B与C的横坐标、纵坐标都不相等

如果在图形a中点A的坐标为(5,3)，则图形b中与A对应的点A'的

4．若点P(x,y)的坐标满足xy0则点P必在（ ）A．原点 B．x轴上 C．y轴上 D．x轴或y轴上 5．点P在x轴上 ，且到y轴的距离为5，则点P的坐标是（ ）

A．(5,0) B．(0,5) C．(5,0)或(-5,0) D．(0,5)或(0,-5)

6.平面上的点(2,-1)通过上下平移不能与之重合的是（ ）

A．(2,-2) B．(-2,-1) C．(2,0) D．2,-3)

7.将△ABC各顶点的横坐标分别减去3，纵坐标不变，得到的△A'B'C'

相应顶点的坐标，则△A'B'C'可以看成△（ ）

A．向左平移3个单位长度得到 B．向右平移三个单位长度得到

C．向上平移3个单位长度得到 D．向下平移3个单位长度得到

8．线段CD是由线段AB平移得到的，点A(-1,4)的对应点为C(4,7),

则点B(-4,-1)的对应点D的坐标是（ ）A．(2,9) B．(5,3) C．(1,2) D．(-9,-4)

9.如图，把图○1中△ABC经过一定的变换得到图○2中的

△A'

B'

C'

，如果图○1的△ABC上点P的坐标是(a,b)，那么这个点在

图○2中的对应点P'的坐标是 （ ） A．(a2,b3) B．(a2,b3) C．(a3,b2) D．(a2,b3)

10．点P(2,-3)先向上平移2个单位长度，再向左平移3个单位长度，得到点P'的坐标是（ ）

A．(-1,-5) B．(-1,-1) C．(5,-1) D．(5,5) 二、填空题 1．在坐标系内，点P（2,－2）和点Q（2,4）之间的距离等于________个单位长度，线段PQ的中点坐标是____________ 2．将点M(2,-3)向左平移2个单位长度，再向下平移1个单位长度，得到的点的坐标为_______

3.在直角坐标系中，若点P(a2,b5)在y轴上，则点P的坐标为

坐标为__________

10．已知线段AB=3，AB∥x轴，若点A的坐标为（1,2）,则点B的

坐标为_________________

三、解答题

如图，在平面直角坐标系中，分别写出△ABC的顶点坐标，并求

出△ABC的面积。

四.第八章 二元一次方程组

1．下列方程组是二元一次方程组的是（ ）．

A．xy14xy1x2x201

xy2B.y2x3C.D.1y yx1x3xy0

2. 二元一次方程2xy7的正整数解有（ ）个。 A. 1 B. 2 C. 3 D. 4

3. 已知方程组5xy35y4和x2y55xby1

有相同的解，则a，b的值

ax为 （ ）

Ａ．a1a4a6a142 Ｂ． Ｃ．b6 Ｄ．bb2

2

b4．买钢笔和铅笔共30支，其中钢笔的数量比铅笔数量的2倍少3

支．若设买钢笔x支，铅笔y支，根据题意，可得方程组（ ）． A．xy30xyy2x3 B．30y2x3 C．xy30xy30x2y3 D． 

x2y3

5、已知甲、乙两人的年收入之比为2：3，年支出之比为4：7，年

终时两人都余了400元，若设甲的年收入为x元，年支出为y元，

则可列方程组( )

xy400xy4002x7y4003x4A34 B 27y400 xy400xy400

2x437C37y400xy400 D．24 6. 已知二元一次方程3x12y1＝0，用含x的代数式表示y为

7. 若方程组4x3y14

kx(k1)y6的解中x、y的值相等，k8、甲、乙二人同解方程组axby2cx3y2，甲正确解得x1

1，乙因

y抄错了c，解得x2

y6，则abc= 9. 已知3x2y17

2x3y13，则x-y= 。 10.若满足方程组3x5ym2

的x

2x3ym，y的值的和等于6，则m的值为 ． 11. 已知3a2b4,2ab5,则85ab____.

12.若3xy52

2xy30，则xy_______。

13．姐姐4年前的年龄是妹妹年龄的2倍，今年年龄是妹妹的1.5倍，则姐姐今年的年龄是 岁。

4(xy1)3(1y)2

14. （8分）解方程组

x2y3

2

15．已知y=x2+px+q，当x=1时，y的值为2；当x=-2时，y的值为

2．求当x=-3时，y的值．

16.上杭县某中学七年级学生外出进行社会实践活动，如果每辆车坐45人，那么有15个学生没车坐；如果每辆车坐60人，那么可以空出一辆车。问共有几辆车，几个学生？

17．甲、乙两人练习跑步，如果甲让乙先跑10米，甲跑5秒钟就可

追上乙；如果甲让乙先跑2秒钟，甲跑4秒钟就能追上乙．求甲乙两人的速度．

18. 服装厂要生产一批某种型号的学生服装，已知3米长的布料可

做上衣2件或裤子3条，一件上衣和一条裤子为一套，计划用600

米长的这种布料生产，应分别用多少布料生产上衣和裤子才能恰好

配套？共能生产多少套？

本文来源：http://www.guakaob.com/xiaoxue/640053.html