北师大版八年级下册数学期末试卷及答案2015

【www.guakaob.com--五年级】

北师大版八年级下册数学期末试卷及答案2015(一)
2015年新北师大版八年级下数学期末考试试卷(有答案)

2015年新北师大版八年级下数学期末考试试卷

1

2

3

4

5

北师大版八年级下册数学期末试卷及答案2015(二)
2015最新北师大版八年级下册数学期末试题

八年级下册数学期末试题

一、选择题（共15小题，每小题3分）

1．无论a取何值时，下列分式一定有意义的是 （ ）

a21A． 2

a

a1B．2

a

a21C．

a1

D．

a1

2

a1

2．已知实数x, y满足x4y80，则以x, y的值为两边长的等腰三角形的周长为（ ）

A．20或16 B．20 C．16 D．以上答案都不对

3．实数a、b、c在数轴上对应的点位置如图所示，下列式子正确的是（ ）

①b+c>0 ②a+b>a+c ③bc<ac ④ab>ac 67 A．1个 B．2个 C．3个

D．4个

4．下列图形中不是中心对称图形的是（ ） A.线段 B.矩形 C.等腰梯形 D.正方形 5．下列运算正确的是（ ） A．

b1b10.5ab5a10b6a1xyyx

2a1 D． B． C． aa0.2a0.3b2a3b3xyyx

6.如果把分式

5x

中的 x,y都扩大7倍，那么分式的值（ ）。

x2y

A. 扩大7倍 B. 扩大14倍 C. 扩大21倍 D. 不变

7．如图，直线l、l、l表示三条相互交叉的公路，现计划建一个加油站，要求它到三条公路的距离相等，则可供选择的地址有 ( ) A．一处 B．二处 C．三处 D．四处 8. 若平行四边形的对角线长度为6,8，一边长为2x-1，则x的取值范围为（ ） A．0<x<4 B．1<x<4 C．0<x<3 D．1<x<3

x84x1

9．将不等式13的解集在数轴上表示出米，正确的是（ ）

x8x22

10．如图，平行四边形ABCD的周长为16 cm，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为（ ）

A．4 cm B．6 cm C．8 cm D．

10cm

11.“5·12”滚川大地震导致某铁路隧道被严重破坏．为抢修其中一段120米的铁路，施工队每天比原计划多修5米，结果提前4天开通了列车．问原计划每天修多少米?某原计划每天修x米，所列方程正确的是（ ）

120120120120

4 B．4 x5xxx5120120120120

4 D．4 C．

x5xxx5

m

1，下列说法正确的是（ ） 12．关x的分式方程

x5

A．

A．m<一5时，方程的解为负数 C．m>一5时，方程的解是正数

B．方程的解是x=m+5 D．无法确定

2x3x31

13．关x的不等式组3x2有四个整数解，则a的取值范同是（ ）

xa4

A．

115115115115

a B．a C．a D．a 42424242

14.如图，在△ABC中，BD、CE是△ABC的中线，BD与CE相交于点O，点F、G分别是BO、CO的中点，连接AO．若AO=6cm，BC=8cm，则四边形DEFG的周长是（ ）

A. 14cm B. 18cm C. 24cm D. 28cm

15.如图：E是边长为1的正方形ABCD的对角线BD上一点，且BE＝BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ＋PR的值是（ ）

（A

）

12

（B） （C

（D

322二、填空题（共6小题，每小题3分）

16.如图，若将四根木条钉成的矩形木框变为平行四边形ABCD的形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的值等于 .

17.如图，有一张直角三角形纸片，两直角边AC=5cm，BC=10cm，将△ABC折叠，点B与点A重合，折痕为DE，则CD的长为________.

18.直线l1:yk1xb与直线l2:yk2x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1xbk2x的解为___________。 19.若xkx

2

1

是一个完全平方式，则k＝

16

xm2

220. 若关于x的分式方程无解，则m的值为___________ x3x3

21. 如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB=5，AC=2，则DF的长为. 三、解答题（共7小题，37分）

22.（3分）分解因式：4(ab)216(ab)2

23.（3分）解方程：

63x5



x1xxx1x21x22x

x,其中x1. 24.（5分）先化简，再求值：2

x2x2x1

2x31

25.（4分）解不等式组x1，并把解集在数轴上表示出来。

2x2

26.（6分）已知，如图在等边△ABC的三边上分别取D，E，F，使得AD=BE=CF， 求证：△DEF是等边三角形

B

27.（8分）某服装厂设计了一款新式夏装，想尽快制作8800件投入市场，服装厂有A、B两个制衣车间，A车间每天加工的数量是B车间的1.2倍，A、B两车间共同完成一半后，A车间突发故障停产，剩下的工作全部由B车间单独完成，结果前后共用20天完成全部任务，求AB两车间每天分别可以加工多少件.

28. （8分）如图，将矩形纸中ABCD沿对角线AC折叠，使点B落在点B的位置，AB与CD相交于点E；

（1）找出一个与△AED全等的三角形，并加以证明；

（2）若AB=8，DE=3，P为线段AC上任一点，PG⊥AE与G，PH⊥EC于H，求PG+PH的值．

附加题：（10分）

如图，梯形ABCD中，AD＝18cm，BC＝21cm

点Q从C点开始沿CB边向B以2cm/s秒，求：

（1）t为何时，四边形ABQP为矩形？ （2）t为何时，四边形PQCD为等腰梯形？

北师大版八年级下册数学期末试卷及答案2015(三)
北师大版八年级下册数学期末考试卷含答案

期末复习题

A卷

一、填空题

1、－3x＜－1的解集是（ ） A、x＜

1 3

B、x＜－

1 3

C、x＞

1 3

2

D、x＞－

1 3

2、下列从左到右的变形是分解因式的是（ ）

A、(x－4)(x+4)=x－16 B、x－y+2=(x+y)(x－y)+2 C、2ab+2ac=2a(b+c) D、(x－1)(x－2)=(x－2)(x－1). 3、下列命题是真命题的是（ ）

A、相等的角是对顶角 B、两直线被第三条直线所截，内错角相等 C、若m4、分式

2

2

2

n2,则mn

D、有一角对应相等的两个菱形相似

ab2，b，的最简公分母是（ ） 222222a2abba2abbab

A、（a²－2ab+b²）（a²－b²）（a²+2ab+b²） B、（a+b）²（a－b）²

C、（a+b）²（a-b）²（a²－b²） D、a

4

b4

5、人数相等的八（1）和八（2）两个班学生进行了一次数学测试，班级平均分和方差如下：

x186，x286，s12259，s22186. 则成绩较为稳定的班级是（

A、八（1）班 B、八（2）班

C、两个班成绩一样稳定 D、无法确定

6、如图1，能使BF∥DG的条件是（ ） A、∠1＝∠3 B、∠2＝∠4 C、∠2＝∠3 D、∠1＝∠4

）

图

1

ABCD在灯泡发出的光照射下形成的影子

是四边形ABCD，若AB:AB1:2，则四边形ABCD的面积∶四边形ABCD的面积为

7、如图2，四边形木框

（ ）

A、4:1 C

． B

图2

D．1:4

8、如图3，A，B，C，D，E，G，H，M，N都是方格纸中的格点（即小正方形的顶点），要使△DEF与△ABC相似，则点F应是G，H，M，N四点中的（ ）

A、H或M C、M或N

B、G或H D、G或M

图3

9、如图，DE∥BC，则下列不成立的等式是（ ）

ADAE

BDECACEC

C、

ABDB

A、

10、直线l1：

B、 D、

ABAC

 ADAEADDE

BDBC

yk1xb与直线l2：yk2x在同一平面

直角坐标系中的图象如图所示，则关于

x

的不等式

k1xbk2x的解为（ ）

A、x＞－1 C、x＜－2 二、填空题

11、计算：（1）（-x）²÷y〃

3

22

3

B、x＜－1

D、无法确定

1y

=____________。

12、分解因式：ab+2ab+ab= 。

13、一组数据：1、2、4、3、2、4、2、5、6、1，它们的平均数为 ，众数为 ，中位数为 ；

14、如图6，某航空公司托运行李的费用与托运行李的重量的关系为一次函数，由图可知行李的重量只要不超过________千克，就可以免费托运。

图6

15、如图7所示：∠A=50°，∠B=30°，∠BDC=110°， 则∠C=______°。

16、一项工程，甲单独做5小时完成，甲、乙合做要2小时，那么乙单独做要_____小时。 三、解答题

17、（每小题6分，共18分）

（1）解不等式组，并把解集在数轴上表示出来

（2）解分式方程：

x1

2 21x≥x；

3

x216

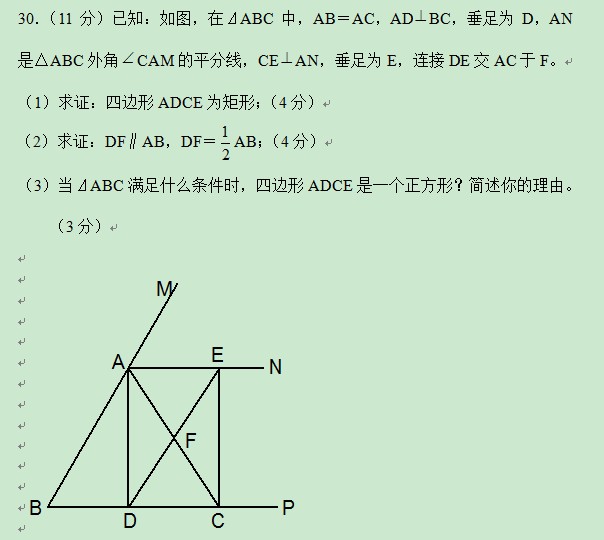
12. x2x4

（3）先化简，再求值：

m414m71

.其中m=5. 122

m9m8m16m3

18、（5分）如图,点D在△ABC的边AB上，连结CD，∠1=∠B，AD=4,AC=5,求 BD 的长?

B

19、（6分）如图9，为了测量旗杆的高度，小王在离旗杆9米处的点C测得旗杆顶端A的仰角为50°；小李从C点向后退了7米到D点（B、C、D

在同一直线上），量得旗杆顶端A的仰角为40°．根据这些数据，小王和小李能否求出旗杆的高度？若能，请写出求解过程；若不能，请说明理由．

图9

20、（7分）八年级某班进行小制作评比，作品上交时间为5月1日至30日，评委把同学上交作品的件数按5天一组分组统计绘制了频数直方图如图所示。一直从左到右各长方形高的比为2:3:4:6:4:1,第三组的频数为12。

（1）本次活动共有多少件作品参评？ （2）哪组上交的作品数量最多？有多少件？

（

3）经过评比，第四组与第六组分别有10件与2件获奖，那么这两组中哪组的获奖率较高？

21、（9分）如图，矩形ABCD中，AB=4，BC=6，M是BC的中点，DEAM，E为垂足。 （1）求△ABM的面积；（2

）求DE的长；（3）求△ADE的面积。

B 卷 一、填空题 22、分式【北师大版八年级下册数学期末试卷及答案2015】

x29的值为0，则x的值为（ ）

x24x3

23、若

a2b22b10，则a

，b＝ 。

24、 C是线段AB的黄金分割点，AB4cm，则AC

．

25、如图，已知△ABC∽△DEF，且相似比为k，则k= ,直线象限．

ykxk的图像必经过

26、观察下列等式：39×41=40—1，48×52=50－2，56×64=60—4，65×75=70－5，83×97=90—7…，请你把发现的规律用字母m,n的代数式表示出来： 。

2

2

2

2

2

2

2

2

2

2

27、在方程组

xym，

中，已知x0，y0，m的取值范围是 。

2xy6

ABC的边AB上的一点，过点D作一条直线，使它与另一边相

28、 (6分)如图，点D是不等边三角形

交截得的三角形与△ABC相似，这样的直线可以作几条？为什么？

29、(10分)某校初中三年级270名师生计划集体外出一日游，乘车往返，经与客运公司联系，他们有座位数不同的中巴车和大客车两种车型可供选择，每辆大客车比中巴车多15个座位，学校根据中巴车和大客车的座位数计算后得知，如果租用中巴车若干辆，师生刚好坐满全部座位；如果租用大客车，不仅少用一辆，而且师生坐完后还多30个座位. ⑴求中巴车和大客车各有多少个座位？

⑵客运公司为学校这次活动提供的报价是：租用中巴车每辆往返费用350元，租用大客车每辆往返费用400元，学校在研究租车方案时发现，同时租用两种车，其中大客车比中巴车多租一辆，所需租车费比单独租用一种车型都要便宜，按这种方案需要中巴车和大客车各多少辆？租车费比单独租用中巴车或大客车各少多少元？

30、（10分）如图，在梯形ABCD中，AD平行BC，BC=3AD。

（1）如图甲，连接AC，如果△ADC的面积为6，求梯形ABCD的面积；

（2）如图乙，E是腰AB上一点，连接CE，设△BCE和四边形AECD的面积分别为S1和S2，且2S1=3S2，求

的值；

（3）如图丙，如果AB=CD，CE⊥AB于点E，且BE=3AE，求∠B的度数。

AE

BE

一、选择题：

二、填空题：

11、

x2y2

12、ab(a—b)2 13、3，2，2.5 14、20 15、30 16、

10 3

三、解答题： 1

19、（6分）解：能求出旗杆的高度．………………（1分）

根据题意可知，在△ABC中，∠ACB=50°，∠B=90°则∠BAC=40°…（2分） 在△ABC与△DBA中 ∠BAC＝40°=∠D ∠B＝∠B

∴△ABC∽△DBA………………（4分）

∴

ABDB

BCAB

，AB2=BC·BD…………………（5分）

又∵BC=9 DB=7+9=16∴AB2=9×16 ∴AB=12（m）

即旗杆的高度为12米．…………（6分） 20、解（1）第三组的频率是

41 …………1分 12÷1=60（件） ∴共有60件作品参评 ………2分



52346415

（2）由图可知，第四组作品数量最多为6×60=18（件） ………………………………3分

20

∴第四组共有作品18件 …………………………4分

（3）第四组获奖率是105……………………………5分 第六组获奖率是

189

21

6020

23

……………………6分

∵

52＜93

∴第六组的获奖率较高 ………………………7分

21、解：如图，矩形ABCD中，∠B=90．

∵M是BC的中点，BC=6，∴BM=3．

SABM

11

ABBM436． ------------3分 22

（2）在Rt△ABM中，

AMAB2BM242325．矩形

ABCD中，AD=BC=6．∵AD∥BC，

24．--------6分 AD．∴DE6．∴∴∠DAM=∠AMB．又∵∠DEA=∠B=90，∴△ADE∽△MAB．∴DEDE

545ABAM

（3）∵△ADE∽△MAB，相似比为AD

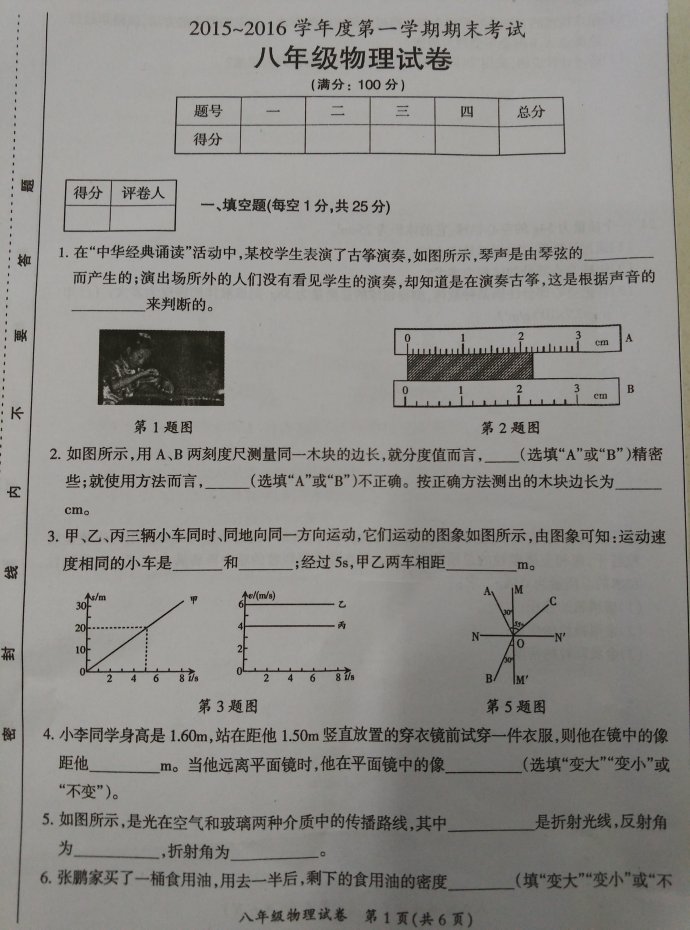
AM



62．∵6，∴SADE

（）

5SMAB5

B卷

SABM6，∴SADE



216．-----------------9分

25

北师大版八年级下册数学期末试卷及答案2015(四)
2014---2015年北师大版最新八年级数学下册期末试卷及答案

2014—2015学年北师大版八年级数学期末

测试题

招贤乡一中 陈艳慧

一、选择题（每小题3分，共24分）

1. 若a<0,则下列不等式不成立的是（ ）

A． a+5＜a+7 B．5a＞7a C．5-a＜7-a D．aa

5

7

2．下列从左到右的变形是因式分解的是（ ）

2

A.（x+1）(x-1)=x-1 B.(a-b)(m-n)=(b-a)(n-m) C.ab-a-b+1=(a-1)(b-1) D.m2-2m-3=m(m-2-3)

m

3．方程2

x3

的解为（ ）X k B 1 . c o m x1

A．2 B．1 C．2 D．1

4．不等式3（2x+5）> 2（4x+3）的解集为（ ）

B．

C．

A． D．

6.在△ABC中，∠C=90°，AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E，且AB=10，则△EDB的周长是（ ）

A.4 B.6 C.8 D.10

A

B

7.在△ABC中，∠ACB=90° ，点O为△ABC的三条角平分线的交点，OD⊥BC，OE⊥AC，OF⊥AB，点D，E，F分别为垂足，且AB=10，BC=8，则点O到三边AB,AC,BC的距离分别是（ ）

A.2，2，2 B.3，3，3 C.4，4，4 D.2，3，5

EB

8.如图，平行四边形ABCD的对角线相交于点O，且AB≠AD，过O作OE⊥BD交BC于点E．若△CDE的周长为10，则

AB+AD的值是（ ）

A.10 B.15 C.25 D.30

二.填空题（每题3分，共24分）

9．分解因式： x2y-y3= .

x21

10．当x 时，分式值为

x－1

0．

11.如图，已知函数y = 3x + b和y = ax - 3的图象交于点P( -2，-5) ，则根据图象可得不等式3x + b ＞ax - 3的解集是 .

2

12.如图，面积为12cm的△ABC沿BC方向平移至△DEF位置，平移的距离是边BC长的两倍，则图中的四边形ACED的面积是______cm．

2

13. 已知两个分式:A

411

,B

X22XX24

.其中x≠2且

x≠-2,则A与B的关系是 .

14.某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需要时间与原计划生产450台机器所需时间相同，现在平均每天生产 台机器.

15. 如图，平行四边形ABCD的周长为36，对角线AC，BD相交于点O，点E是CD的中点，BD=12，则⊿DOE的周长为 .

B

16. 如图，Rt△ABC中，∠ABC=90°，BC=3，AC=4，AB的垂直平分线DE交BC的延长线于点E,则CE的长为

.

三、解答题（本大题7个小题，共72分） 17.（12分）分解因式：

222

(1)－4ax+12ax－9x (2) (2x+y) – (x+2y)

18.（9

x10

分）解不等式组，并写出该不等式组x2

x23

的最大整数解.【北师大版八年级下册数学期末试卷及答案2015】

119．（9分）先化简a

a1a你喜欢的数代入求值.

20.（9分）解方程x

x2

2

a1



2a1a

，然后给a选择一个

2

1 x24

21.(10分)如图，OC是∠AOB的平分线，点P为OC上一点，若∠POD+∠PEO=180°，试判断PD和PE的大小关系，并说明理由.

北师大版八年级下册数学期末试卷及答案2015(五)
2015年新北师大版八年级数学下册期中试卷及答案

八年级下册 数学期中测试卷

一、选择题（每小题3分，共30分）

B．C．△AOD≌△EOD D．△AOD≌△BOC

9.不等式5x－1＞2x+5 的解集在数轴上表示正确的是( ).

1．如图可以看作正△OAB绕点O通过( )旋转所得到的. A、3次 B、4次 C、5次 D、6次 2． 在平行四边形、等腰梯形、等腰三角形、矩形、菱形五个图形中，既

10.如图，点E是平行四边形ABCD的边CD的中点，AD、BE的延长线相交于点F，DF=3，

DE=2，则平行四边形ABCD的周长为( ). A．5 B．7 C．10 D．14x2＞0，3． 不等式组

x21≥x3的解集是（ ）

A．x≥8

B．x＞2 C．0＜x＜2

D．2＜

x≤8

4．若把不等式组2x≥，



的解集在数轴上表示出

x≥形为（ ）.

A．长方形 B．线段 C．射线 D．直线 5.不等式x2的解集在数轴上表示为 ( ).

6.不等式1＋x＜0的解集在数轴上表示正确的是（ ）.

A． B．

C． D．

7.如图，在四边形ABCD中，对角线AB=AD，CB=CD，

若连接AC、BD相交于点O，则图中全等三角形共有（ ）.

A．1对 B．2对 C．3对 D．4对

AD

E【北师大版八年级下册数学期末试卷及答案2015】

8 .如图(三)所示，点E是矩形ABCD的边AD延

长线上的一点，且AD=DE，连结BE交CD于

O

点O，连结AO.下列结论不正确的是( ).

B

CA．△AOB≌△BOC B．△BOC≌△EOD

1

来，则其对应的图

二、填空题（每小题3分，共21分）

1．不等式2x－3≥x的解集是． 2.若关于x的不等式（1－a）x＞2可化为x＜

2

1a

，则a的取值范围

是 . 3. 一元一次不等式组



3x20

0

的解集是 .

x14．如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上，下

列结论：①CE＝CF②∠AEB＝750

③BE+DF＝EF④S正方形ABCD＝2+，其中正确的序号

是 。

（把你认为正确的都填上）

5

．如图，已知

BC=EC

，∠BCE=∠ACD，要使△ABC≌△DEC，则应添加的一个条件

为 ．（不唯一，只需填一个）

6.如图，AB=AC，要使△ABE≌△ACD，应添加的条件是．

7、如图，四边形ABCD平移到四边形A'B'C'D'的位置，这时可把四边形A'B'C'D'看作先将四边形

ABCD向右平移格，再向下平移 三、解答题（共49分）

1、（8分）解不等式组：2(x1)3,



x10x.,并把解集表示在数轴上。

3(x1)5x2、（8分）解不等式组

1x12

2x4，并指出它的所有的非负整数解.

3、（8分）已知x3是关于x的不等式3x

ax22x

23

的解，求a的取值范围。

4．（8分） 如图，已知，EC=AC，∠BCE=∠DCA，∠A=∠E；求证：BC=DC． 5、（8分）如图所示，在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90º后的图形△A¹B¹C¹

2

6．（9分） 雅安地震后，政府为安置灾民，从某厂调拔了用于搭建板房的板材5600m3和铝材2210m3,计划用这些材料在某安置点搭建甲、乙两种规格的板房共100间.若搭建一间甲型 板房或

请你根据以上信息，设计出甲、乙两种板房的搭建方案.

最新北师大版 八年级下册 数学期中测试卷

一、选择题（每小题3分，共30分）

一．选择题

1．C 2．B 3．D 4．B 5．C 6. A 7.A 8. A. 9. C

10. D

二、填空题（每小题3分，共24分）

1．x≥3 2. a＞1.

3.2

3

x1 4． ①②④. 5．（答案不唯一，只需填一个） 7． 三、解答题

1．(2013浙江湖州,18,8分)解不等式组：

2(x1)3,

x10x.

【思路分析】分别求出各不等式的解集，再求出其公共解集即可．

【解】

2(x1)3,

x10

x.

由①，得x52

． 由②，得x5．

所以原不等式组的解是5

2

x5．

3(x1)5x12、解不等式组

x12

2x4，并指出它的所有的非负整数解.

【思路分析】先解不等式组，得到公共解集合，然后在此范围内取非负整数解.

3(x1)5x1【解】①x12

2x4②

3

由①得：x2„„„„„„„„„„„„„„„„„„„„„„„2分

由②得：x

7

3

„„„„„„„„„„„„„„„„„„„„„„„4分 ∴原不等式组的解集是-2x7

3

„„„„„„„„„„„„„„5分

∴原不等式组的非负整数解为0,1,2. „„„„„„„„„„„„„6分

3．（2013四川凉山州，19，6分）已知x3是关于x的不等式3x

ax222x

3

的解，求a的取值范围。

【思路分析】先把x3代入关于x的不等式3xax222x

3

得到关于a的不等式从而求出a的取值范围

来*~源中国教育出版网&%]

【解】x3代入关于x的不等式3xax222x

3

， 解这个不等式得a4, ∴a的取值范围是a4.

4．（2013广东珠海，14，6分）如图，已知，EC=AC，∠BCE=∠DCA，∠A=∠E； 求证：BC=DC．

5.略

6．[2013湖南邵阳，24，8分]雅安地震后，政府为安置灾民，从某厂调拔了用于搭建板房的板材5600m3和铝材2210m3,计划用这些材料在某安置点搭建甲、乙两种规格的板房共100间.若搭建一

请你根据以上信息，设计出甲、乙两种板房的搭建方案.

知识考点：一元一次不等式组的实际应用.

审题要津：设搭建甲种板房x间，则搭建乙种板房(100 –x)间.则所打间板房100间所需板材数量为甲型板材数量+乙型板材数量≤5600，所需铝材数量为甲型铝材数量+乙型铝材数量≤2210. 满分解答：解：设搭建甲种板房x间，则搭建乙种板房(100 –x)间.

40x+60(100-x)≤5600

根据题意，得.

30x+20(100- x)≤2210

解这个不等式组，得20≤x≤21. 因为x是整数，所以x=20,或x=21.

所以搭建方案有：搭建甲种板房20间，乙种板房80间；搭建甲种板房21间，乙种板房79

间.

4

北师大版八年级下册数学期末试卷及答案2015(六)
2015年北师大版八年级数学下册期末试卷

    2014~2015学年度第二学期即将要结束了,小编为大家整理了2015年北师大版八年级数学下册期末试卷.希望各位同学能够动手锻炼一下,巩固下知识点.提前祝各位同学取得好成绩!更多的八年级下册试卷及答案请及时关注中国招生考试网!!!
【点击进入】全国八年级下册数学期末试卷汇总

2015年北师大版八年级数学下册期末试卷（一）

2015年北师大版八年级数学下册期末试卷（二）

2015年北师大版八年级数学下册期末试卷（三）

2015年北师大版八年级数学下册期末试卷（四）

2015年北师大版八年级数学下册期末试卷（五）

2015年北师大版八年级数学下册期末试卷（六）

本文来源：http://www.guakaob.com/xiaoxue/640860.html