【www.guakaob.com--一年级】
海淀区八年级第二学期期末练习
数 学
(分数:100分时间:90分钟) 2016.7
学校 班级 姓名 成绩
一、选择题:(本题共30分,每小题3分)
在下列各题的四个备选答案中,只有一个是正确的. ....1.下列各式中,运算正确的是
A
.3 B
C
.D
2
2.下列各组数中,以它们为边长的线段不能构成直角三角形的是 A.1
.3,4,5C.5,12,13D.2,2,3
3.如图,矩形ABCD中,对角线AC,BD交于O点.若∠AOB=60°, AC=8,则AB的长为 A.4B
. C.3D.5
4.已知P1(-1,y1),P2(2,y2)是一次函数yx1图象上的两个点,则y1,y2的大小关系是 A.y1y2 B.y1y2 C.y1y2 D.不能确定
5.2022年将在北京—张家口举办冬季奥运会,很多学校开设了相关的课程.下表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差s
2根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择 A.队员1 B.队员2 C.队员3 D.队员4 6.用配方法解方程x22x30,原方程应变形为 A.(x1)22
B.(x1)24C.(x1)24D.(x1)22
7.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为 A.13 B.14 C.15 D.16
8.一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则8min时容器内的水量为 A.20 L B.25 L C.27L D.30 L
9.若关于x的方程kx2(k1)x10的根是整数,则满足条件的整数k的个数为 A.1个B.2个 C.3个 D.4个
10.如图1,在菱形ABCD中,∠BAD=60°,AB=2,E是DC边上一个动点,F是AB边上一点,
∠AEF=30°.设DE=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的
A.线段EC B.线段AE C.线段EF D.线段BF
图1图2
二、填空题:(本题共18分,每小题3分) 11.写出一个以0,1为根的一元二次方程.
12.若关于x的一元二次方程x24xm0有两个不相等的实数根,则m的取值范围是. 13.如图,为了检查平行四边形书架ABCD的侧边是否与上、下边
都垂直,工人师傅用一根绳子比较了其对角线AC,BD的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理.
14.若一次函数ykxb(k0)的图象如图所示,点P(3,4)在函数图象
上,则关于x的不等式kxb≤4的解集是.
15.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,
若AB=5,BC=8,则EF的长为.
16.如图,正方形ABCD的面积是2,E,F,P分别是AB,BC,AC上
的动点,PE+PF的最小值等于.
D
P
C
F
A
E
B
三、解答题:(本题共22分,第17—19题每小题4分,第20—21题每小题5分) 17
.计算:
18.解方程:y(y4)12y.
19.已知x1是方程x23axa20的一个根,求代数式3a29a1的值.
20.在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5). (1)求此一次函数的表达式;
(2)若点P为此一次函数图象上一点,且△POB的面积为10,求点P的坐标.
21.如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面
积.
四、解答题:(本题共10分,第22题5分,第23题5分) 22.阅读下列材料:
北京市为了紧抓疏解非首都功能这个“牛鼻子”,迁市场、移企业,人随业走.东城、西城、海淀、丰台„„人口开始出现负增长,城六区人口2016年由升转降.
而现在,海淀区许多地区人口都开始下降。统计数字显示:2015年该区常住外来人口约为150万人,同比下降1.1%,减少1.7万人,首次实现了负增长.
和海淀一样,丰台也在2015年首次实现了常住外来人口负增长,同比下降1.4%,减少1.2万人;
东、西城,常住外来人口同样呈下降趋势:2015年东城同比下降2.4%,减少5000人,西城则同比下降5.5%,减少1.8万人;
石景山,常住外来人口近年来增速放缓,预计到2016年年底,全区常住外来人口可降至63.5万,比2015年减少1.7万人,首次出现负增长; „„
2016年初,市发改委透露,2016年本市将确保完成人口调控目标——城六区常住人口较2015年下降3%,迎来人口由升转降的拐点.
人口下降背后,是本市紧锣密鼓疏解非首都功能的大战略. 根据以上材料解答下列问题:
(1)石景山区2015年常住外来人口约为万人;
(2)2015年东城、西城、海淀、丰台四个城区常住外来人口同比下降率最高的是区;根据材料
中的信息估计2015年这四个城区常住外来人口数最多的是区;
(3)如果2017年海淀区常住外来人口降到121.5万人,求从2015年至2017年平均每年外来人
口的下降率.
23.如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF. (1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
五、解答题:(本题共20分,第24题6分,第25—26题每小题7分)
24.如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的
大小为α,面积记为S.
(1)请补全下表:
(2)填空:
由
(
1)可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,
不妨把单位菱形的面积S记为S(α).例如:当α=30°时,SS(30)SS(135)
1
;当α=135°时,2
S(60)S( ______°);S(150)S( ______°),„,由此可以归纳出S(180)S().
(3)两块相同的等腰直角三角板按图2的方式放置,ADAOB=α,试探究图中两个带
阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
图2
八年级第二学期期末练习
数 学 答 案 2016.7
一、选择题(本题共30分,每小题3分)
二、填空题(本题共18分,每小题3分)
11.x2x0
或
x(x1)0(答案不唯一);
12.m
4;
13.对角线相等的平行四边形是矩形,矩形的四个角都是直角;(“矩形的四个角都是直角”没写不扣分) 14.x≤3;
15.
3
; 16 2
三、解答题(本题共22分,第17—
19题每小题4分,第20—21题每小题5分) 17.解:原式=2=
----2分 =3 -------------------------------------------------------------------------------3分 = = -----------------------------------------------------------------------------------------4分 18.解:y22y10, --------------------------------------------------------------------------------------1分
(y1)20, ------------------------------------------------------------------------------------------3分
y1y21. -------------------------------------------------------------------------------------------4分
19.解法一:
解:∵x1是方程x23axa20的一个根,
∴13
aa20. ---------------------------------------------------------------------------------------1分
∴a23a1. --------------------------------------------------------------------------------------2分 ∴3a29a13(a23a)1 --------------------------------------------------------------------3分
3(1)12. -----------------------------------------------------------------4分
解法二:
解:∵x1是方程x23axa20的一个根,
∴ 13aa20. ---------------------------------------------------------------------------------------1分
∴a23a10. ------------------------------------------------------------------------------------2分 解方程得a
. -------------------------------------------------------------------------------3分
把a
代入得3a29a1得3a29a12. ----------------------------------------4分 20.解:(1)设此一次函数的表达式为ykxb(k0).
∵一次函数的图象经过点A(2,3)与点B(0,5),
2kb3, ∴ -----------------------------------------------------------------------------------1分
b5.
k1,解得
b5.
∴此一次函数的表达式为yx5.----------------------------------------------------3分 说明:求对k给1分,求对b给1分. (2)设点P的坐标为(a,a5). ∵B(0,5), ∴OB=5.
∵S△POB=10, 1
∴5|a|10. 2
∴|a|4.
∴a4.
∴点P的坐标为(4,1)或(4,9). ----------------------------------------------5分 说明:两个坐标每个1分.
21.解:连接AC,过点C作CE⊥AB于点E. ∵AD⊥CD,
∴∠D=90°.
在Rt△ACD中, AD=5, CD=12,
AC
13. ---------------------------------------------------------1分 ∵BC=13,
∴AC=BC. -----------------------------------------------2分 ∵CE⊥AB, AB=10, ∴AE=BE=
11
AB=105. ----------------------3分 22
在Rt△CAE中,
CE
12. -----------------4分
E
11
∴S四边形ABCD=S△DAC+S△ABC=5121012306090. -----------------5分
22
四、解答题(本题共10分,第22题5分,第23题5分)
22.(1)65.2; -----------------------------------------------------------------------------------------------1分 (2)西城; 海淀;(每空1分) ------------------------------------------------------------------3分 (3)解:设海淀平均每年常住外来人口的下降率为x.
由题意,得
150(1x)2121.5. ---------------------------------------------------------------------4分
解得,x10.110%, x21.9.(不合题意,舍去)
答:海淀平均每年常住外来人口的下降率为10%. -----------------------------------------5分
23.(1)证明:∵四边形ABCD是矩形,
∴AD=BC, ∠D=∠BCD=90°. ∴∠BCF=180°-∠BCD=180°-90°=90°.
∴∠D=∠BCF. ----------------------------------------------------------------------1分 在Rt△ADE和Rt△BCF中,
FAEB,
ADB.C【海淀区八年级第二学期期末练习数学2016.7】
∴Rt△ADE≌Rt△BCF. ---------------------------------------------------------2分 ∴∠1=∠F. ∴AE∥BF. ∵AE=BF,
∴四边形ABFE是平行四边形. ---------------------------------------------------3分
(2)解:∵∠D=90°,
∴∠DAE+∠1=90°.
∵∠BEF=∠DAE, ∴∠BEF+∠1=90°.
∵∠BEF+∠1+∠AEB=180°, ∴∠AEB=90°. --------------------------------------------------------------------------4分
在Rt△ABE中, AE=3,BE=4, AB
5. ∵四边形ABFE是平行四边形,
∴EF=AB=5. --------------------------------------------------------------------------5分
五、解答题(本题共20分,第24题6分,第25—26题每小题7分) 24.(1
1;.(说明:每对两个给1分) ----------------------------------2分
2
(2)120;30;α. -----------------------------------------------------------------------------------4分
(说明:前两个都答对给1分,最后一个α答对给1分) (3)答:两个带阴影的三角形面积相等.
证明:将△ABO沿AB翻折得到菱形AEBO, 将△CDO沿CD翻折得到菱形OCFD. ∴S△AOB= S△CDO=
11
S菱形AEBO=S(α) ---------------------------------------------------5分 22
11
S菱形OCFD=S(180) -----------------------------------------6分 22
由(2)中结论S(α)=S(180) ∴S△AOB=S△CDO.
25.(1)①依题意补全图形
.
②解法1: 证明:连接CE.
∵四边形ABCD是正方形, ∴∠BCD=90°, AB=BC. ∴∠ACB=∠ACD=
---------------------------------------------------------1分
1
∠BCD=45°. 2
∵∠CMN=90°, CM=MN, ∴∠MCN=45°.
∴∠ACN=∠ACD+∠MCN=90°. ∵在Rt△ACN中, 点E是AN中点, ∴AE=CE=
1
AN. ----------------------------------------------------------------------------2分 2
∵AE=CE, AB=CB,
∴点B,E在AC的垂直平分线上. ∴BE垂直平分AC.
∴BE⊥AC. --------------------------------------------------------------------------------------3分 解法2: 证明:连接CE.
∵四边形ABCD是正方形, ∴∠BCD=90°, AB=BC. ∴∠ACB=∠ACD=
1
∠BCD=45°. 2
∵∠CMN=90°,CM=MN, ∴△CMN是等腰直角三角形. ∴∠MCN=45°.
∴∠ACN=∠ACD+∠MCN=90°. ∵在Rt△ACN中, 点E是AN中点, ∴AE=CE=
1
AN. 2
在△ABE和△CBE中,
AECE,
ABCB, BEBE.
∴△ABE≌△CBE(SSS). -----------------------------------------------------------------2分 ∴∠ABE=∠CBE. ∵AB=BC,
∴BE⊥AC. --------------------------------------------------------------------------------------3分 (2)BE
1
+CN(或2BE
+CN). ---------------------------------------4分 2
证明:∵AB=BC, ∠ABE=∠CBE,
∴AF=FC. ∵点E是AN中点, ∴AE=EN.
∴FE是△ACN的中位线. ∴FE=
1
CN. 2
∵BE⊥AC, ∴∠BFC=90°. ∴∠FBC+∠FCB=90°. ∵∠FCB=45°, ∴∠FBC=45°. ∴∠FCB=∠FBC. ∴BF=CF.
在Rt△BCF中, BF2CF2BF2, ∴BF
BC. --------------------------------------------------------------------------------5分 ∵四边形ABCD是正方形, ∴BC=AD. ∴BF
AD. ∵BE=BF+FE, ∴BE
(3)
1
AD+CN. ----------------------------------------------------------------------6分 2
3
. ---------------------------------------------------------------------------------------------------7分
4
海淀区八年级第二学期期末练习
物 理 2016.7 学校 班级 姓名 成绩
题2分)
1. 以著名物理学家的名字作为“压强”单位的是
A.帕斯卡(Pa) B.牛顿(N) C.瓦特(W) D.焦耳(J)
2. 如图1所示的实例中,目的是为了增大压强的是
A.载重汽车装有很多轮子 B.书包背带做的很宽 C
.图钉帽的面积做得较大 D.注射
器
针头做得很尖 图1
3.运动员推铅球,铅球离手后在空中运动的过程中(不计空气阻力),其受力情况是
A.只受推力
B.只受重力
C.受推力和重力
D.不受任何力
4.如图2所示的四种用具在正常使用的过程中,属于省力杠杆的是
A.用夹子夹取盘子
B.托盘天平
图2 C.用筷子夹食品 D.用起子起瓶盖
5. 图3所示的四个实例中,目的是为了减小摩擦的是
A.用力握紧球拍 B.瓶盖上刻有纹线 C.旱冰鞋下装有滚轮 图3 D.运动员戴上防滑手套
6.下列现象中与大气压有关的是
A.水杯中的水对杯底产生压强 B.吸盘可以压在光洁的墙面上
C.熟透的苹果从树上落到地上 D.吊车将重物吊上高楼
7.下列事例中,物体运动状态不变的是
A.火车启动时,从静止变为运动
B.在地面上滚动的小球,速度逐渐变小
C.重物被吊车沿直线向上匀速吊起
D.行驶在盘山公路上保持速度大小不变的汽车
8.将一个装有水的U型管倾斜放置,图4中的水面状况符合实际的是
C A B D 图4
9.晓晗刚学完液体内部压强规律,一次喝完盒装酸奶后,想利用废纸盒做个小实验,他在 空纸盒的侧面的不同高度处扎三个大小一样的孔,将纸盒装满水后,水从小孔喷出。图 5中的几种水流现象最接近实际情况的是
A B 图
5 C D
10.两人站在海边的沙滩上,在沙滩上留下了深浅不同的脚印,如图6所示,则下列说法正确
的是
A.两人对沙滩的压强一定相同
B.脚印小的人对沙滩的压强一定大
C.脚印深的人对沙滩的压力一定大 图6 D.脚印深的人对沙滩的压强一定大
11.在亚洲西部,巴勒斯坦和约旦交界处,有一个面积约为810平方公里的内陆盐湖,由于湖水
中含有高浓度的盐分,致使水中没有鱼虾、水草,人们称之为“死
海”。然而令人惊叹的是,即使是不会游泳的人,也能浮在水面上,
真是“死海不死”。一个成人漂浮在“死海”上,如图7所示,人所受
浮力大小约为
图
7 A.6N B.60N C.600N D.6000N【海淀区八年级第二学期期末练习数学2016.7】
12. 下列关于压力和压强的说法正确的是( )
A. 压力的方向总是竖直向下的
B. 压力的大小总是和重力大小有关
C. 在铁轨下面铺设枕木是为了减小对地面的压力
D. 相对较小的压力可能产生很大的压强
13.下面关于功、功率、机械效率说法正确的是
A.功率大的机械做功一定多
B.功率大的机械做功一定快
C.机械做功少,功率一定小,机械效率一定低
D.做有用功多的机械,机械效率一定高
14.在中国科技馆内有如图8所示的展品,小火车匀速向左行驶,将要通过横跨火车轨道的小
桥时,从车厢上的小孔竖直向上抛出一个小球,小球在
空中运动一段时间后,落回到火车上并恰好进入原来的
小孔内。对于这一现象下列说法正确的是
A.小球能够落到原来的小孔是由于小火车具有惯性
B.小球在空中运动的速度大小是不变的
C.小球能够落到原来的小孔是由于小球具有惯性 图8
D.小球从抛出到落回的过程中运动状态保持不变
15.水平桌面上放置甲乙两个完全相同的杯子,杯中分别盛有不同浓度的
盐水,将同一个鸡蛋先后放入其中,当鸡蛋静止时,两个杯子中液面恰好相平,鸡蛋所处的位置如图9所示,则
A.乙杯底部所受的液体压强较大
B.甲杯底部所受的液体压力较大
C.鸡蛋在甲杯中受到浮力较大 甲 乙
图9 D.桌面所受压力一样大
二、多项选择题(下列各小题均有四个选项,其中符合题意的选项均多于一个。共12分,每小
题3分。每小题选项全选对的得3分,选对但不全的得2分,有错选的不得分)
16. 图10所列的物品在使用过程中应用了连通器原理的是
A.茶壶 B.电茶炉的水位计
图10 C.洗手池下水的回水管 D.将墨水吸入笔管中
17.关于运动和力,下列说法正确的是
A.用力推讲桌没有推动,讲桌受力一定不平衡
B.水中的小鱼受到水向上的压力一定大于向下的压力
C.从树上自由落下的苹果,对地球一定有吸引力的作用

19.如图12甲所示,重为G、底面积为S的圆柱形容器(不计容器壁的厚度)放置在水平桌面
上,容器内装有密度为ρ、重为G1的液体;将体积为V、重为G2的长方体物块A用细线系好,使A浸没在液体中,如图12乙所示,此时细线对
物块A的拉力为F,下列说法正确的是
A.甲图中,容器底部所受液体的压强为G1
B.乙图中,液体对物块A作用的合力大小为F-ρgV
C.乙图中,物块A所受的重力与拉力的合力大小是ρgV
图12 D.乙图中,容器对桌面的压力为G+G1+G2-F
三、实验与探究题(共40分,20-29、34、35题各2分,30、32、33、36题各3分,31题4 分。)
20.在图13中,画出实心球在空中运动时所受重力G的示意图。
21.如图14所示,O点为杠杆的支点,请画出力F的力臂,并用字母L表示
22.若用一个定滑轮和一个动滑轮组成滑轮组提升重物A,请你用划线代替绳子组装图15 所示的滑轮组。
23.图16所示的弹簧测力计的示数是N。
图15 图14 图13
24.如图17所示,把重物放在平直的塑料板上,塑料板变弯曲,这个现象说明:力可以产生的
作用效果之一是使物体发生 。
S
图18 图19
图17
25.小烨同学为班级联欢会准备气球,当他将两个充好气的气球挤压在一起时,发现两个气球
都发生了形变,如图18所示,这个现象说明力的作用是 。
26.将适量橡皮泥包裹在吸管下端,制成了一个土密度计。将此土密度计依次放入盛有不同液
体的甲、乙容器中,土密度计静止的状态如图19所示,可以判断 容器中的液体密度较大。(选填“甲”或“乙”) 27.小华同学通过实验探究某种液体内部的压强p与深度h的关系,根
据实验数据绘出了如图20所示的图像。由图像可知,该液体20cm深处的压强为Pa;并且由图像可以得出该液体50cm深处的压强为 Pa。
图20
28.小红同学做“探究杠杆的平衡条件”的实验。组装好实验器材后发现杠杆的状态如图21所示。
(1)若要使杠杆在水平位置平衡,需把杠杆右端的平衡螺 右
母向 端移动(选填“左”或“右”);
(2)使杠杆在水平位置平衡后,在杠杆的位置A处挂2个
钩码。为了使杠杆在水平位置重新平衡,应该在位置
B处挂(每个钩码的质量都相等)
图
21 29.小明用如图22所示的装置探究同一直线上二力合成的规
律时,把橡皮筋的下端B用细线固定在铁架台的横杆上,上端A通
过细绳挂在弹簧测力计的挂钩上; 将一个重为2N的钩码通过细绳挂在橡皮筋的A端,用弹簧测 力计竖直向上将橡皮筋的A端拉到O点,并在竖直放置的白板上标
记O点的位置,记录此时弹簧测力计的示数F1和挂钩码的细绳对A 端的拉力F2; 摘掉钩码,用弹簧测力计将橡皮筋的A端仍拉到O点,记录此
时弹簧测力计的示数F。 (1)实验中先后两次都将橡皮筋的A端拉伸到O点,是为了让F与
F1和F2的 相同。 图22
(2)如果以上实验中弹簧测力计的示数F1=4.6N,则F=N。
30.在探究液体内部压强特点时,小阳用包有橡皮膜的金属盒(作为探头)与U型管(作为压
强计)相连通进行实验。
(1)使用前应检查装置是否漏气,当用手指按压(不论
是重压还是轻压)橡皮膜时,发现U型管两边的液
面的高度差几乎不变,则说明该装置 (选填 A
“漏气”、“不漏气”)。 B
(2)装置调整好后,若将探头先后放在同一容器的A、
图23
B两处,实验现象分别如图23甲、乙所示,则可以
判断出A、B两处的压强pA pB(选填“大于”、“等于”或“小于”)。由此可以得 到的结论是:液体内部的压强与 有关。
31.图24是验证阿基米德原理的实验过程示
意图,依次读出甲、乙、丙、丁图中弹簧
测力计的示数分别为F1、F2、F3、F4。由
这些测量量,可知石块受到的重力
为 ;由甲、乙两个图的弹
簧测力计的示数可以求出石块受到浮力
F浮到的重力G排= 。如果满足甲
乙 图24 丙 丁
关系式 ,即可验证阿基米德原理。(各空均用测量量表示)
海淀区八年级第二学期期末练习
数 学
(分数:100分 时间:90分钟) 2016.7
学校 班级 姓名 成绩
一、选择题:(本题共30分,每小题3分)
在下列各题的四个备选答案中,只有一个是正确的. ....1.下列各式中,运算正确的是
A
.3 B
C
.D
2
2.下列各组数中,以它们为边长的线段不能构成直角三角形的是 A.1
.3,4,5C.5,12,13D.2,2,3
3.如图,矩形ABCD中,对角线AC,BD交于O点.若∠AOB=60°, AC=8,则AB的长为 A.4B
. C.3D.5
4.已知P1(-1,y1),P2(2,y2)是一次函数yx1图象上的两个点,则y1,y2的大小关系是 A.y1y2 B.y1y2 C.y1y2 D.不能确定
5.2022年将在北京—张家口举办冬季奥运会,很多学校开设了相关的课程.下表记录了某校4名同学短道速滑选拔赛成绩的平均数与方差s
2 根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择 A.队员1 B.队员2 C.队员3 D.队员4 6.用配方法解方程x22x30,原方程应变形为 A.(x1)22
B.(x1)24C.(x1)24D.(x1)22
7.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为 A.13 B.14 C.15 D.16【海淀区八年级第二学期期末练习数学2016.7】
8.一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则8min时容器内的水量为 A.20 L B.25 L C.27L D.30 L
9.若关于x的方程kx2(k1)x10的根是整数,则满足条件的整数k的个数为 A.1个 B.2个 C.3个 D.4个
10.如图1,在菱形ABCD中,∠BAD=60°,AB=2,E是DC边上一个动点,F是AB边上一点,
∠AEF=30°.设DE=x,图中某条线段长为y,y与x满足的函数关系的图象大致如图2所示,则这条线段可能是图中的
A.线段EC B.线段AE C.线段EF D.线段BF
图1图2
二、填空题:(本题共18分,每小题3分) 11.写出一个以0,1为根的一元二次方程.
12.若关于x的一元二次方程x24xm0有两个不相等的实数根,则m的取值范围是. 13.如图,为了检查平行四边形书架ABCD的侧边是否与上、下边
都垂直,工人师傅用一根绳子比较了其对角线AC,BD的长度,若二者长度相等,则该书架的侧边与上、下边都垂直,请你说出其中的数学原理.
14.若一次函数ykxb(k0)的图象如图所示,点P(3,4)在函数图象
上,则关于x的不等式kxb≤4的解集是.
15.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,
若AB=5,BC=8,则EF的长为.
16.如图,正方形ABCD的面积是2,E,F,P分别是AB,BC,AC上
的动点,PE+PF的最小值等于.
D
P
C
F
A
E
B
三、解答题:(本题共22分,第17—19题每小题4分,第20—21题每小题5分) 17
.计算:
18.解方程:y(y4)12y.
19.已知x1是方程x23axa20的一个根,求代数式3a29a1的值.
20.在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5). (1)求此一次函数的表达式;
(2)若点P为此一次函数图象上一点,且△POB的面积为10,求点P的坐标.
.
21.如图,四边形ABCD中,AB=10,BC=13,CD=12,AD=5,AD⊥CD,求四边形ABCD的面
积.
四、解答题:(本题共10分,第22题5分,第23题5分) 22.阅读下列材料:
北京市为了紧抓疏解非首都功能这个“牛鼻子”,迁市场、移企业,人随业走.东城、西城、海淀、丰台„„人口开始出现负增长,城六区人口2016年由升转降.
而现在,海淀区许多地区人口都开始下降。统计数字显示:2015年该区常住外来人口约为150万人,同比下降1.1%,减少1.7万人,首次实现了负增长.
和海淀一样,丰台也在2015年首次实现了常住外来人口负增长,同比下降1.4%,减少1.2万人;
东、西城,常住外来人口同样呈下降趋势:2015年东城同比下降2.4%,减少5000人,西城则同比下降5.5%,减少1.8万人;
石景山,常住外来人口近年来增速放缓,预计到2016年年底,全区常住外来人口可降至63.5万,比2015年减少1.7万人,首次出现负增长; „„
2016年初,市发改委透露,2016年本市将确保完成人口调控目标——城六区常住人口较2015年下降3%,迎来人口由升转降的拐点.
人口下降背后,是本市紧锣密鼓疏解非首都功能的大战略. 根据以上材料解答下列问题:
(1)石景山区2015年常住外来人口约为万人;
(2)2015年东城、西城、海淀、丰台四个城区常住外来人口同比下降率最高的是区;根据材料
中的信息估计2015年这四个城区常住外来人口数最多的是区;
(3)如果2017年海淀区常住外来人口降到121.5万人,求从2015年至2017年平均每年外来人
口的下降率.
23.如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF. (1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
五、解答题:(本题共20分,第24题6分,第25—26题每小题7分)
24.如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的
大小为α,面积记为S.
(1)请补全下表:
(2)填空:
由(
1
)
可以发现单位正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,
不妨把单位菱形的面积S记为S(α).例如:当α=30°时,SS(30)SS(135)
1
;当α=135°时,2
.由上表可以得到S(60)S( ______°);S(150)S( ______°),„,由此可以归纳出S(180)S().
(3) 两块相同的等腰直角三角板按图2的方式放置,ADAOB=α,试探究图中两个
带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
图2
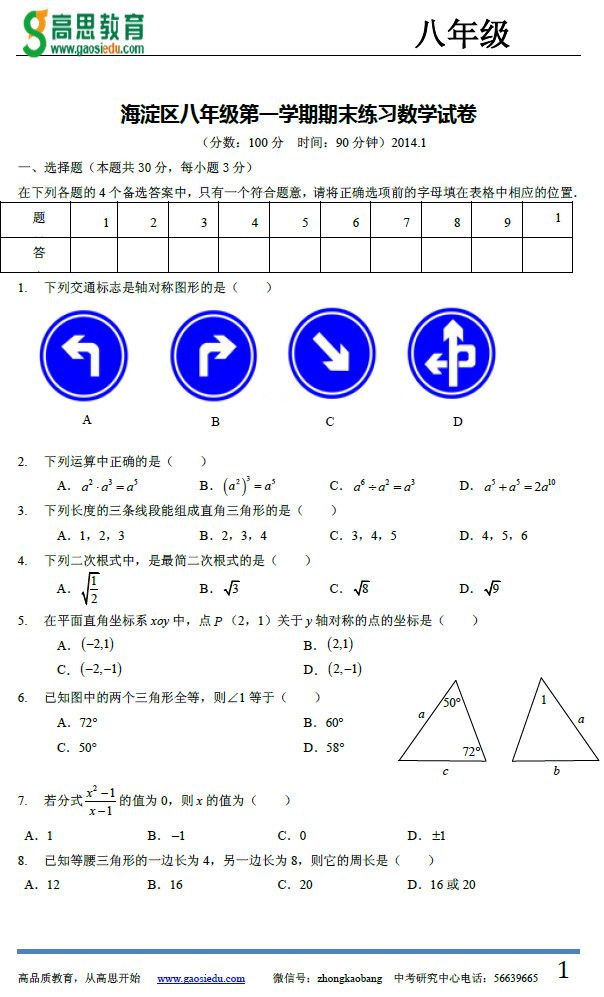
海淀区八年级第一学期期末练习
数 学 2016.1
(分数:100分 时间:90分钟)
学校 班级 姓名 成绩 一、选择题:(本题共36分,每小题3分)
在下列各题的四个备选答案中,只有一个是正确的. 请将正确选项前的字母填在表格中相应的位置.
1.下列图形中,不是轴对称图形的是 ..
(A) (B) (C) (D
) 2.下列运算中正确的是
824
(A)2x3y5xy (B)xxx
3262363
(C)(xy)xy (D)2xx2x
3.在平面直角坐标系xOy中,点P(-3,5)关于x轴的对称点的坐标是
(A) (3,5) (B)(3,-5) (C)(5,-3) (D)(-3,-5) 4x的取值范围是 (A)x ≠-
2223
(B)x<-
(C)x≥-
(D)x≥
2333
5.下列各式中,从左到右的变形是因式分解的是
(A)3x3y53(xy)5 (B)(x1)(x1)x1 (C)x2x1(x1) (D)x(xy)xxy 6.下列三个长度的线段能组成直角三角形的是
(A)1 (B)1 (C)2,4,6 (D)5,5,6
2
2
2
2
7.计算2(3) ,结果为
(A)6 (B)6 (C)6 (D)66 8.下列各式中,正确的是
bb2b1
(B)
a2ba2aa2ababa2a24
(C) (D)
a2(a2)2cc
(A)
9.若xm与2x的乘积中不含x的一次项,则实数m的值为 (A)2 (B)2 (C)0 (D)1
10.如图,在△ABC和△CDE中,若ACBCED90,AB=CD,BC=DE,则下列结论中不正确的是 ...
(A)△ABC ≌ △CDE (B)CE=AC (C)AB⊥CD (D)E为BC中点
11.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形. 如果大正方形的面积是25,小正方形的面积是1,直角三角形的两条直角边的长分别是a和b,那么(ab)的值为
(A)49 (B)25 (C)13 (D)1
2
1111
12.当x分别取2014、2013、2012、….、2、1、0、1、、、…、、、
2320122013
x21
时,计算分式2的值,再将所得结果相加,其和等于 2014x1
1
(A)1 (B)1 (C)0 (D) 2014 二、填空题:(本题共24分,每小题3分)
13.若实数x、
yy20,则xy的值为2b
14.计算:3
5a
15
.比较大小:16.分解因式:3a312a= .
2
17.如图,△ABC≌△DEF,点F在BC边上,AB与EF相交于点P.若DEF37,PB=PF,则APF °. 18.如图,△ABC是等边三角形,点D为 AC边上一点,以BD为边作等边△BDE, 连接CE.若CD=1,CE=3,则BC=_____. 19.在平面直角坐标系xOy中,点A、点B的坐标分别为(-6,0)、(0,8).若△ABC是以∠BAC为顶角的等腰三角形,点C在x轴上,则点C的坐标为
20.如图,分别以正方形ABCD的四条边为边,向其内部作等边三角形,得到△ABE、△BCF、△CDG、△DAH,连接EF、FG、GH、HE.若AB=2,则四边形EFGH的面积为三、解答题:(本题共14分,第21题5分,第22题9分) 21.计算:
22.(1)解方程:
1
()1(
2)0+2
x2
1. x1x
xx24x4x
)(2))先化简,再求值:(,其中x2. x2x2x24
上一篇:北师大九年级下圆复习导学案
下一篇:期末考试6年2015