【www.guakaob.com--四年级】
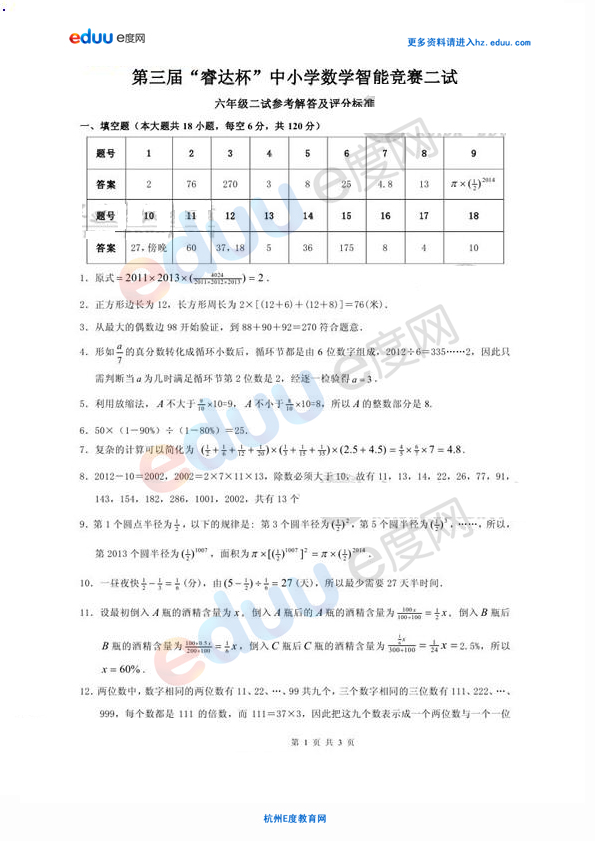
2014年第五届“睿达杯“六年级数学第二试
时间:90分钟 满分:150分
一、填空题(本大题共青18小题,每空6分,计120分)
231、143÷47=_________ 59
2、最多能取________个两两不等的正整数,使是其中任意三个数之和都为质数。
3、如图四边形ABCD为正方形,三角形EBC为等边三角形,那么角x的度数是_______
4、六张大小不同的小正方形纸片拼成图中的所示的图形,已知最小的正方形面积是1,那么图中红色正方形的面积是__________
A
D红
S1
B
(第3题)S2C(第4题)
(第5题)
55、如图,半圆S1的面积是14.13平方厘米,圆S2的面积是19 平方厘米,那么长方形(阴影部分)8
的面积是________平方厘米。(∏取3.14)
6、一列客车从甲站开往乙站,速度为65千米/小时,一列货车从乙站开往甲站,速度为60千米/小时,已知货车比客车早开出5分钟,两车相遇点距甲乙两站的中点10千米,甲乙两站之间的距离是_______千米。
7、甲、乙两人步行的速度比是7:5,甲、乙分别由A、B两地出发,如果相向而行,0.5小时后相遇;如果他们同向而行,那么甲追上乙需要_______小时。
8、公园举行菊花展览,门票每张20元,降价后游客人数是原来的2倍,收入增加了20%,一张门票降价_________元。
9、如图是一个立体图形,叫四面体,它有四个面都是三角形,有六条棱(边),把每条棱都染成白色、蓝色或红色,为了使每一个三角形都至少有一条红色的边,那么最少有______条棱要染成红色。
10、如图,边长为8和10的两个正方形并放在一起,则三角形AMC的面积是_________
A
15.75m2
(第9题)
(第10题)(第11题)
11、从一块正方形土地中,划出一块宽为1米的长方形土地(见图),剩下的长方形面积是15.75平方米,那么划出的长方形土地的面积是_______平方米
12、甲、乙两个圆柱体容器,底面积之比为4:3,甲容器水深为7厘米,乙容器水深为3厘米,再往两个容器注入同样多的水,直到水深相等,这时水深________厘米。
113、某班一次集会,请假人数是出席人数的 ,中途又有一人请假离开,这样一来,请假人数是出席9
人数的3 ,那么这个班共有_________人。 22
14、一个容器内装满水,现有大、中、小三种铁球,第一次把小球沉入水;第二次把小球取出,把中球沉入水中;第三次把中球取出,把小球和大球一起沉入水中。已知每次从容器中溢出水量的情况是:第二次是第一次的2倍,第三次是第二次的1.5倍。则大球的体积是小球体积的________倍。
15、某商场为招览顾客举办购物抽奖,奖金有三种:一等奖1000元,二等奖250元,三等奖50元,共100人中奖,奖金总额为9500元,那么二等奖有_____名。
16、从A城到B城有一条快客线路,全程行驶时间为44分钟,到达总站后,司机至少休息10分钟,快客就调头行驶。如果这条线路A、B两边总站每隔9分钟都发一辆(不必是同一时间),则这条线路至少需要________辆快客。
17、容器中有某种浓度的酒精,加入一杯水后,容器中纯酒精含量为25%;再加入一杯纯酒精,容器中纯酒精含量为40%。问原来容器中有________杯酒精,浓度是_________。
18、如图,第一个图形是一个水平摆放的小正方体木块,第2个图形和第3个图形是由这样的小正方体木块叠放而成的。按照这样的规律继续叠放下去,那么第7个图中,从正面看,看得到的木块应有_________块,看不到的木块应有_________块。
二、解答题(本大题共2小题,每小题15分,共30分)
1、如图所示是一个用牛皮纸紧绕成的纸筒,纸筒长是40厘米,外直径是38厘米,中间有一直径是18厘米的轴洞,已知牛皮纸的厚度是0.5毫米。请回答:
(1)这筒纸展开后是个怎么样的图形?
(2)这筒纸展开后的长度与原图中什么有关?
(3)这筒纸展开后大约有多少米?(∏取3.14)
12、某酒店自助餐标价,男宾价130元,女宾价100元,儿童价60元,现在有 的成人各带一个孩子,3
总共收了2160元餐费,问:这次活动共有多少人参加?

2015年睿达杯数学邀请赛模拟试题
六年级 第Ⅰ试试题(参考答案)
2015年11月1日 上午8:30至10:00
一、以下每题6分,共120分
21153735105解析:原式= 1072149137
2.计算: 101100110001)= 。
248
4671
解析:原式=(101+1001+10001)+()=11105
8888()1.计算:0.3÷1= 。
3.一个时钟时针长5cm,它从6点到8点24分,时针扫过的面积是多少?
8点24分-6时=2.4时; 3.14×5 2 × 1 12 ×2.4, =3.14×25×0.2, =15.7(平方厘米);
答:时针扫过的面积是15.7平方厘米.
4.一箱乒乓球,一等品占
1a
,二等品占(a为自然数),三等品是91只,共有几只乒乓球?。 45
91÷(1-1/4-2/5)
=91÷7/20 =260
箱子里共有260个乒乓球
图1
5.如图1,边长为12cm的正方形与直径为16cm的圆部分重叠(圆心是正方形的一个顶点),用S1,S2分别表示两块空白部分的面积,则S1—S22(圆周率取3)。 解析:差不变面积问题。
S1—S2=(S1+S阴)—(S2+S阴)=S圆—S正=3×(16÷2)2 —122=192—144=48cm2
1
6.图书馆内座无虚席,一节课后,看书的走了8,又进来21人,这时座位不够了,只好有12人两人挤
在一起座一个凳子,学校图书馆共有多少个座位?
7.有一口无水的井,用一根绳子测井的深度,将绳对折后垂到井底,绳子的一端高出井口9m;将绳子三折后垂到井底,绳子的一端高出井口2m,则绳长 米,井深 米。
解析:盈亏问题。绳子分去2段井深,则多2×9=18米,绳子分去三段井深,则多3×2=6米。 井深:(18—6)÷(3—2)=12米,绳长:2×12+18=42米。
8.张阿姨和李阿姨每月的工资相同,张阿姨每月把工资的30%存入银行,其余的钱用于日常开支,李阿姨每月的日常开支比张阿姨多10%,余下的钱也存入银行,这样过了一年,李阿姨发现,她12个月存入银行的总额比张阿姨少了5880元,则李阿姨的月工资是 元。 解析:分数应用题。李阿姨每月的工资为单位“1”。
李阿姨日常开支:(1—30%)×(1+10%)=77%,存银行1—77%=23% 李阿姨的月工资是5880÷12÷(30%—23%)=7000元
9.如右图,ABCD是一个梯形,E是AD的中点,直线CE把梯形分成甲、乙两部分,它们
的面积之比是10∶7.求上底AB与下底CD的长度之比.
3:14
10.在一个两位数的中间加上小数点,得到一个小数,若这个小数与原来的两位数的和是86.9,则原来两位数是 。
解析:数字和倍问题。原来两位数是86.9÷(1+0.1)=79 本题也可用算式谜解答。【睿达杯第五届六年级真题】
11.A,B两校的男、女生人数的比分别为8:7和30:31,两校合并后男、女生人数的比是27:26,则A,B两校合并前人数比是

解析:比和比例。设A,B两校的男、女生人数分别为8a、7a,30b、31b,根据题意有 (8a+30b):(7a+31b)=27:26 189a+837b=208a+780b 所以a=3b
A,B两校合并前人数比(8+7)×3b:(30+31)b=45:61
12.有2013名学生参加数学竞赛,共有20道竞赛题,每个学生有基础分25分,此外,答对一题得3分,不答题得1分,答错一题扣1分,则所有参赛学生得分的总和是 数(填“奇”或“偶”)。 解析:奇偶问题。每一名学生的得分都可以用25+3x+y-z表示,且x+y+z=20,根据三数和为偶数,可知这三个数奇偶性只有2种情况:三个都是偶数,两个奇数一个偶数,不管那种情况,每个学生最终得分都是奇数。2013个奇数相加和还是奇数,则所有参赛学生得分的总和是奇数。
13.从12点开始,经过时针与分针第一次成90°角;12点之后,时针与分针第二次成90°
角的时刻是 。【睿达杯第五届六年级真题】
解析:时钟问题。分针每分钟走360÷60=6度,时针每分钟走30÷60=0.5度,第一次成90度角,即分
4
分。时针与分针第二次成90°,即分针比时针夺走270度,11
11
270÷(6—0.5)=49分,此时为12点49分。
1111
针比时针夺走90度,90÷(6—0.5)=16
14.有一个温泉游泳池,池底有泉水不断涌出,要想抽干满池的水,10台抽水机需工作8小时,9台抽水机需工作9小时,为了保证游泳池水位不变(池水既不减少,也不增多),则向外抽水的抽水机需
解析:牛吃草问题。只需求出每小时新增水即可,设一台抽水机1小时抽1份水。
每小时新增水:(9×9—10×8)=1,所以只需要1台抽水机将新增水抽调就能保证游泳池水位不变。 15.分子与分母的和是2013的最简真分数有 解析:数论问题。
分子与分母的和是2013分数有:
123456789101003100410051006
,,共20122011201020092008200720122012201220121010100910081007
1006个数。
2013=3×11×61,只要分子是2013质因数的倍数时,这个分数就不是最简分数,因为分子分母相加和为2013,若分子是3、11或61的倍数,则分母一定也是是3、11或61的倍数(两数和是某数A的倍数,则这两个数都是A的倍数,或这两个数除以A的余数相加等于A)
[1006÷3]=335,([A]表示不超过A的最大整数,取整) [1006÷11]=91,[1006÷61]=16, [1006÷3÷11]=30,[1006÷3÷61]=5,[1006÷11÷61]=1, 1006—335—91—16+30+5+1=600
即1~1006中有600个数不是3或11或61的倍数的数,所以分子与分母的和是2013的最简真分数有600个。
16.若一个长方体,长是宽的2倍,宽是高的倍,所有棱长之和是56,则此长方体的体积是。 解析:立体图形。高:56÷4÷(1+2+4)=2,此长方体的体积是2×(2×2)×(2×4)=64
17.图4中阴影部分的两段圆弧所对应的圆心分别为点A和点C,AE=4m,点B是AE的中点,那么阴影部分的周长是 m,面积是 m2(圆周率取3)。 解析:图形面积与周长。
周长:4+3×4×2÷4+3×2×2÷4=13m
面积:容斥原理(重叠),两个扇形相加减去长方形 3×42÷4+3×22÷4—2×4=7m2
没有获奖。”他们的话中只有一句是真话,则获奖的是 。
解析:逻辑推理。用相悖论。只有一人说真话,甲,丙话相悖,必有一真一假。 若甲说真话,则乙也说真话,不合题意。则丙是真话,乙说谎,即乙获奖! 19.某小学的六年级有学生152名,从中选男生人数的
D 图4 C
18.某次数学竞赛,甲、乙、丙3人中只有一人获奖,甲说:“我获奖了。”乙说:“我没获奖。”丙说:“甲
1
和5名女生去参加演出,该年级剩下的男、女11
解析:列方程解应用题。设男生有x名,根据剩下男女人数相等可列方程
152—x—5=(1-解得x=77
1)x 11
也可用数论知识枚举得解。
10
,说明男生剩余整拾人,所以女生也剩余整拾人,则参加演出的学生人数位数为2,可能选11
1
出男生7人,17人等,根据总人数,可知只有7满足,所以男生有7÷=77人
11
男生剩余
20.甲、乙两人分别从A、B两地同时出发,相向而行,甲乙两人的速度比是4:5,相遇后,如果甲的速度降低25%,乙的速度提高20%,然后继续沿原方向行驶,当乙到达A地时,甲距离B地30km,那么A、B两地相距km。
解析:与分数比相关的行程问题。设全程为“1”。 相遇时甲走全程的
445
,乙走全程的。 4599
54412
=,此时甲又走了全程的×= 99929
相遇后甲、乙速度比:4×(1—25%):5×(1+20%)=1:2 当乙到达A地时,已又走了全程的1—所以A、B两地相距30÷(1—
42
—)=90km 99
附加题(每题10分,共20分)
1.小红整理零钱包时发现,包中有面值为1分,2分,5分的硬币共有25枚,总值为0.60元,则5分的硬币最多有 枚。 解析:不定方程和方程组。
设1分,2分,5分的硬币分别为x枚,y枚,z枚 则有
x+y+z=25 x+2y+5z=60
两式相减的y+4z=35,显然z最大为8。
2.A、B、C、D四个箱子中分别装有一些小球,现将A箱中的部分小球按如下要求转移到其他三个箱子中:该箱中原有几个小球,就再放入几个小球,此后,按照同样的方法依次把B、C、D箱中的小球转移到其他箱子中,此时,四个箱子都各有16个小球,那么开始时装有小球最多的是 箱,其中装有小球 个。 解析:列表倒推法
上一篇:人教版四年级下册英语音频
下一篇:数学题六年级下册卷子